Содержание
- 3. Тема 2. Анализ переходных процессов классическим методом Лекция 3 (2 часа) Изучаемые вопросы: 3.1. Законы коммутации
- 4. 3.1. Законы коммутации
- 6. Метод «классический» отражает использование в нем решений дифференциальных уравнений с постоянными параметрами методами классической математики. Данный
- 7. Операторный метод — это метод расчёта переходных процессов в электрических цепях, основанный на переносе расчёта переходного
- 8. 3.2. Начальные условия, порядок определения независимых и зависимых начальных условий
- 9. 3.3. Принужденные (установившиеся) и свободные составляющие переходного процесса
- 10. 3.4. Анализ переходных процессов в цепях с одним реактивным элементом классическим методом. Постоянная времени цепи Исследование
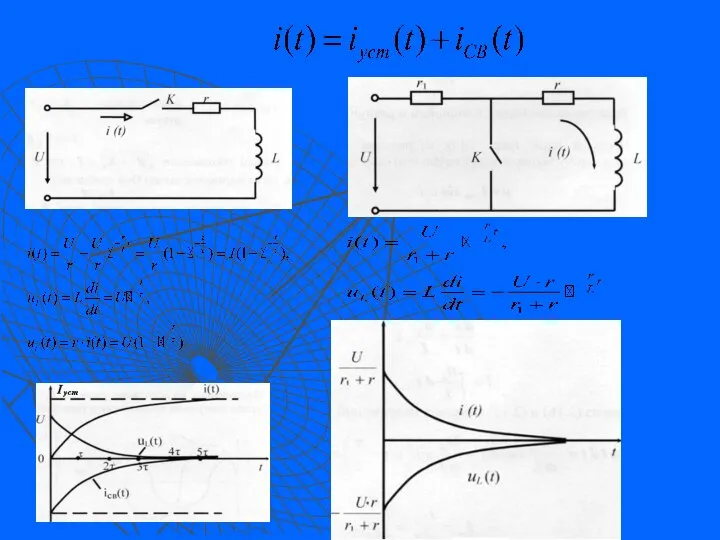
- 11. 3.4.1. Переходный процесс в активно-индуктивной цепи Уравнение (3) описывает переходный процесс, возникающий в цепи r, L
- 12. 3.4.2. Короткое замыкание цепи r, L
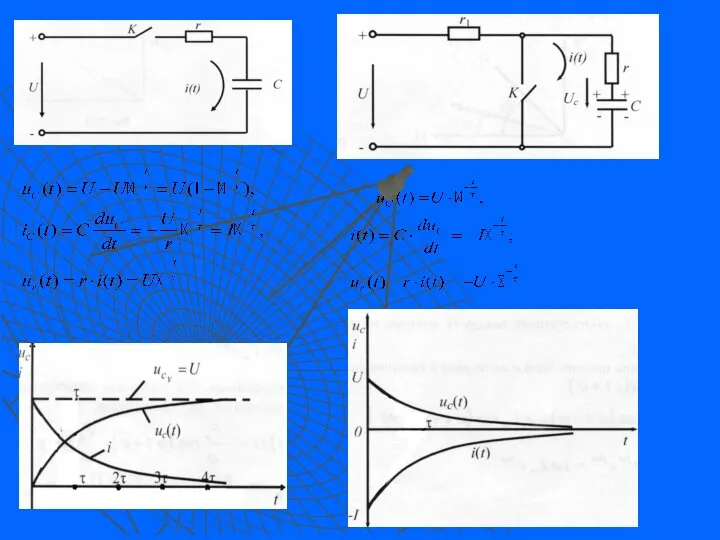
- 13. 3.4.3. Переходный процесс в активно-емкостной цепи. Заряд конденсатора
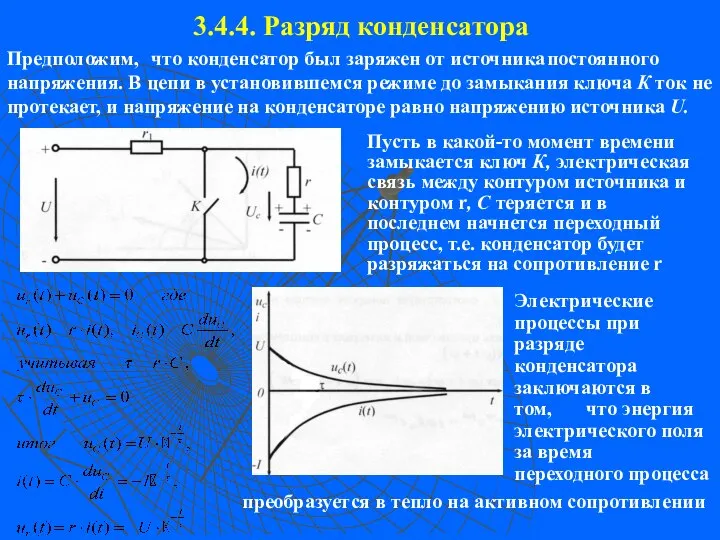
- 14. 3.4.4. Разряд конденсатора Предположим, что конденсатор был заряжен от источника постоянного напряжения. В цепи в установившемся
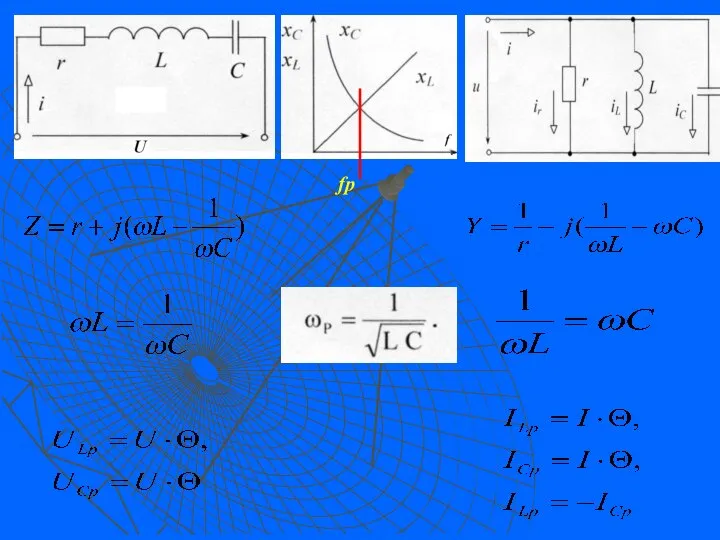
- 15. 3.4.5. Постоянная времени цепи
- 18. Переходные процессы в R-L-C цепи Уравнение Кирхгофа для этой цепи после замыкания ключа S Возьмем производную
- 20. Скачать презентацию













 Печатное устройство HP DeskJet GT 5810/5820
Печатное устройство HP DeskJet GT 5810/5820 Год науки и технологий
Год науки и технологий Кофе Пётр Великий Пётр Великий в зёрнах. 100г, 250г, 500г, 500г, 1000г Смесь отборных зёрен разных сортов Арабики средней обжарки. Пётр Велик
Кофе Пётр Великий Пётр Великий в зёрнах. 100г, 250г, 500г, 500г, 1000г Смесь отборных зёрен разных сортов Арабики средней обжарки. Пётр Велик Человек и природа в лирике М.Ю.Лермонтова
Человек и природа в лирике М.Ю.Лермонтова 8 Букви е, и в особових закiнченнях
8 Букви е, и в особових закiнченнях Семейство Крестоцветные
Семейство Крестоцветные Государственная символика России и Чувашской Республики
Государственная символика России и Чувашской Республики Тест: Туристский поход с проверкой туристских навыков. АУ Управление спортивных сооружений Республики Марий Эл
Тест: Туристский поход с проверкой туристских навыков. АУ Управление спортивных сооружений Республики Марий Эл Учитель физики, химии и информатики МОУ СОШ с.Каринка Кирово-Чепецкого района
Учитель физики, химии и информатики МОУ СОШ с.Каринка Кирово-Чепецкого района  Технический анализ товарных и финансовых рынков Индикаторы
Технический анализ товарных и финансовых рынков Индикаторы МИР КАК ФОРМА И ПОТРЕБЛЕНИЕ
МИР КАК ФОРМА И ПОТРЕБЛЕНИЕ Моя семья – моё богатство Семья Орловых
Моя семья – моё богатство Семья Орловых Куприенко Игорь Витальевич Член Координационного совета
Куприенко Игорь Витальевич Член Координационного совета ВОДА
ВОДА Название презентации
Название презентации Переправа
Переправа Электронное правительство. Международные рейтинги и критерии оценки.
Электронное правительство. Международные рейтинги и критерии оценки. Парфюм от Эйвон Тудей
Парфюм от Эйвон Тудей Распознавание растений разных отделов
Распознавание растений разных отделов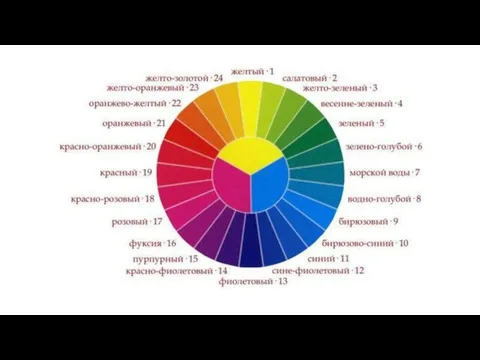 Цветовой круг
Цветовой круг Профессия - пластический хирург
Профессия - пластический хирург Использование технологии дополненной реальности в образовании
Использование технологии дополненной реальности в образовании Мастер – класс Изготовление картин из цветного опила
Мастер – класс Изготовление картин из цветного опила Family memory book
Family memory book  ТЕМА: «Кто такие птицы?»
ТЕМА: «Кто такие птицы?» Делаем отчет. Занятие 8
Делаем отчет. Занятие 8 Викторина
Викторина Восстановление автомобильных деталей сваркой и наплавкой
Восстановление автомобильных деталей сваркой и наплавкой