Слайд 2План лекции 3
Определитель и его свойства (продолжение)
Применение определителей
Невырожденные матрицы
Решение сист.

лин. уравнений с помощью обратной матрицы для невырожденного случая
Снова о ранге матрицы
Правило (формула) Крамера
Слайд 3Одна геометрическая интерпретация

Слайд 4Все-таки, для чего нужен определитель?

Слайд 5Определитель и обратная матрица

Слайд 6Определитель и обратная матрица

Слайд 7Определитель и обратная матрица

Слайд 8Определитель и обратная матрица

Слайд 9Определитель и обратная матрица

Слайд 16Определитель и обратная матрица
Определение 4. Из элементов, взятых из k строк и

k столбцов, любой матрицы (не обязательно квадратной) составим квадратную подматрицу порядка k. Определитель такой квадратной подматрицы называют минором k-го порядка.
Если подматрица составлена из строк и столбцов с одинаковыми номерами (например, из строк с номерами {1, 5 ,7,8}, столбцов с номерами {1, 5, 7, 8}), то минор такой подматрицы называют главным.
Лемма 1. Для любой матрицы если все миноры k-го порядка равны нулю, тогда все миноры порядка больше k также равны нулю.
Доказательство леммы очевидно и непосредственно следует из разложения определителя по формуле Лапласа. Поскольку любой определитель порядка k+1 согласно формуле разложения по Лапласа вычисляется с помощью определителей (миноров) k-го порядка.
Слайд 23Определитель и обратная матрица. Правило Крамера

Слайд 24Определитель и обратная матрица. Правило Крамера

Слайд 26Домашнее задание
Все ответы можно найти
в учебнике [Ал_Пи] - «Алескеров_Пиантковский» (Глава 4)
Найти
![Домашнее задание Все ответы можно найти в учебнике [Ал_Пи] - «Алескеров_Пиантковский» (Глава](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1008495/slide-25.jpg)
обратные матрицы [АлПи]
3. [АлПи] Найти матрицу X (подсказка: уравнение справа
умножить на обр. матрицу, которая справа от X )
Слайд 27Домашнее задание
10.[Ал_Пи] Найти необходимое и достаточное условия пересечения след. трех линий в
![Домашнее задание 10.[Ал_Пи] Найти необходимое и достаточное условия пересечения след. трех линий](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1008495/slide-26.jpg)
одной точке.
(non-singular – невырожденная )
























![Домашнее задание Все ответы можно найти в учебнике [Ал_Пи] - «Алескеров_Пиантковский» (Глава](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1008495/slide-25.jpg)
![Домашнее задание 10.[Ал_Пи] Найти необходимое и достаточное условия пересечения след. трех линий](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1008495/slide-26.jpg)

 Презентация на тему Очерк жизни и творчества
Презентация на тему Очерк жизни и творчества  TROS.2
TROS.2 Торговая Марка
Торговая Марка Урок 35. Придаточные предложения образа действия и степени.
Урок 35. Придаточные предложения образа действия и степени. В. Г. Распутин
В. Г. Распутин Сибирь, Алтайский край, Косихинский район. Именно здесь прошли детские и юношеские годы будущего космонавта 2 - Германа Степановича
Сибирь, Алтайский край, Косихинский район. Именно здесь прошли детские и юношеские годы будущего космонавта 2 - Германа Степановича Экономическое районирование России (9 класс)
Экономическое районирование России (9 класс) Чего ты хочешь…^3^
Чего ты хочешь…^3^ Окружной проезд, владение 10Б, ВАО Соколиная гора
Окружной проезд, владение 10Б, ВАО Соколиная гора Ярмарка домашней и фермерской продукции, авторских украшений, подарков и игрушек
Ярмарка домашней и фермерской продукции, авторских украшений, подарков и игрушек Задачи на расчет количества теплоты
Задачи на расчет количества теплоты Презентация на тему Производные предлоги
Презентация на тему Производные предлоги Дерматология: первичный прием.
Дерматология: первичный прием. Друзья Если плачет кто – то рядом, Если слезы льются градом, Подойдите вы к нему И спросите «Почему?» Это, дети, сделать надо – Плох
Друзья Если плачет кто – то рядом, Если слезы льются градом, Подойдите вы к нему И спросите «Почему?» Это, дети, сделать надо – Плох Батырлык дәресе “Кайнар йөрәк”
Батырлык дәресе “Кайнар йөрәк” Швейцарские банки
Швейцарские банки proektirovanie_bd_na_osnove_normalizatsii_teoria_polnaya
proektirovanie_bd_na_osnove_normalizatsii_teoria_polnaya Ребенок в школе
Ребенок в школе А.П Платонов «Никита»
А.П Платонов «Никита» Python 01_multi_new
Python 01_multi_new Экспериментальные модели артериальной гипертензии
Экспериментальные модели артериальной гипертензии В мастерской кондитера
В мастерской кондитера Конфликт
Конфликт Презентация на тему Африка растительный и животный мир
Презентация на тему Африка растительный и животный мир 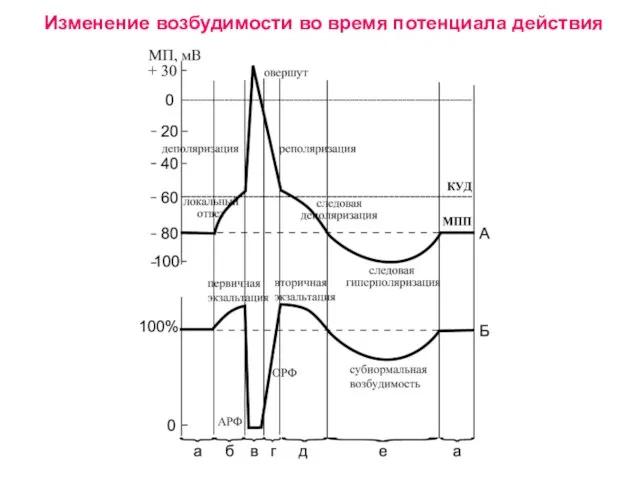 Изменение возбудимости во время потенциала действия
Изменение возбудимости во время потенциала действия Общение в Интернете
Общение в Интернете Внешнее строение листа
Внешнее строение листа Уважаемые родители!
Уважаемые родители!