Теорема о вписанном угле в окружность.

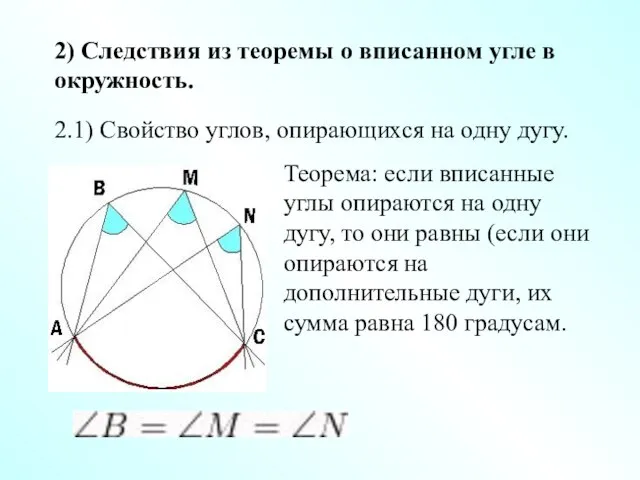
2) Следствия из теоремы о вписанном угле в окружность.
2.1) Свойство углов, опирающихся на одну дугу.
Теорема: если вписанные углы опираются на одну дугу, то они равны (если они опираются на дополнительные дуги, их сумма равна 180 градусам.

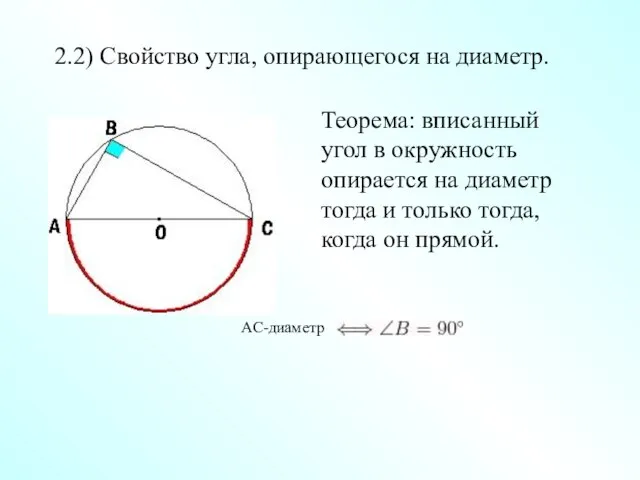
2.2) Свойство угла, опирающегося на диаметр.
Теорема: вписанный угол в окружность опирается на диаметр тогда и только тогда, когда он прямой.
AC-диаметр

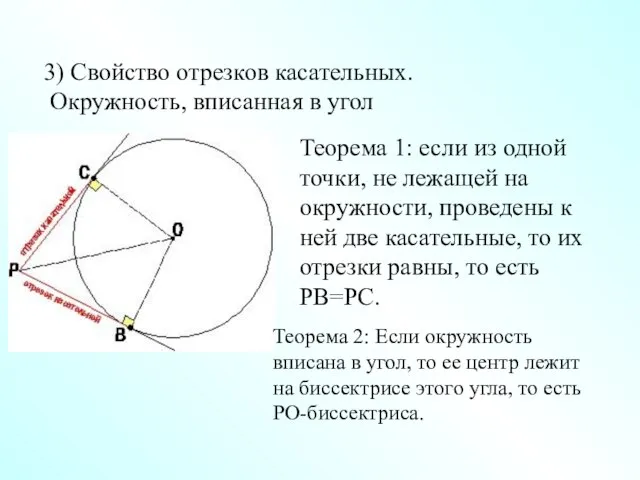
Теорема 1: если из одной точки, не лежащей на окружности, проведены к ней две касательные, то их отрезки равны, то есть PB=PC.
3) Cвойство отрезков касательных.
Окружность, вписанная в угол
Теорема 2: Если окружность вписана в угол, то ее центр лежит на биссектрисе этого угла, то есть PO-биссектриса.

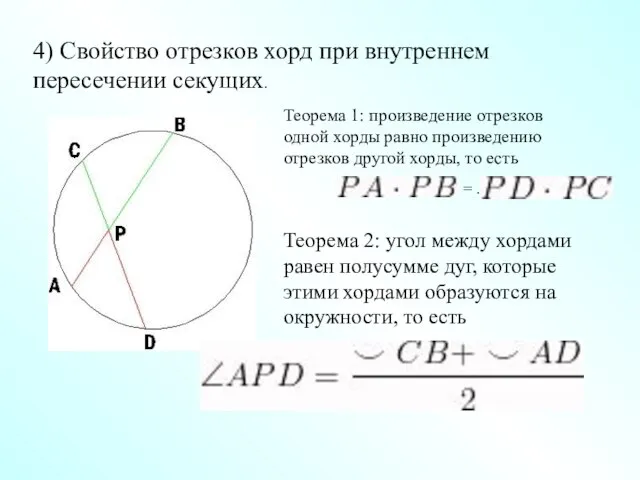
4) Свойство отрезков хорд при внутреннем пересечении секущих.
Теорема 1: произведение отрезков одной хорды равно произведению отрезков другой хорды, то есть
= .
Теорема 2: угол между хордами равен полусумме дуг, которые этими хордами образуются на окружности, то есть

5) Свойство отрезков хорд при внешнем пересечении секущих.
Теорема 1: произведение отрезков одной секущей равно произведению отрезков другой, то есть
=
Теорема 2: угол между секущими равен полуразности соответствующих им дуг, то есть

6) Свойства квадрата отрезка касательной
Теорема 1: Квадрат отрезка касательной равен произведению отрезков секущей, то есть
Теорема 2:угол между касательной и секущей равен полуразности соответствующих им дуг, то есть

7) Угол между касательной и секущей
Теорема: угол между касательной и секущей, проведенными из одной точки окружности, равен половине дуги, которую отсекает секущая (половине центрального угла, соответствующего данной дуге).

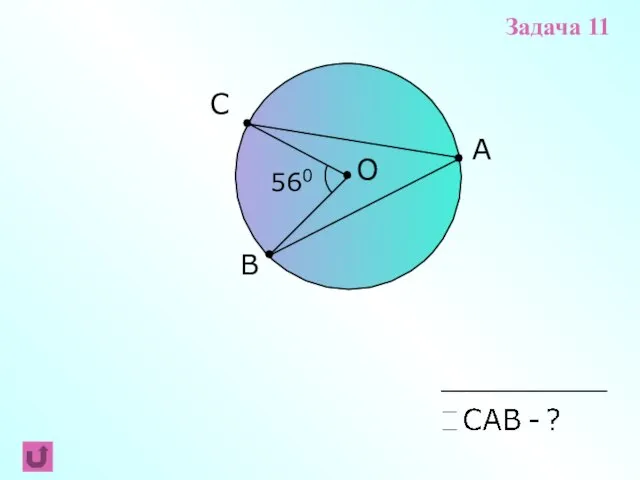
A
В
С
560
О
Задача 11

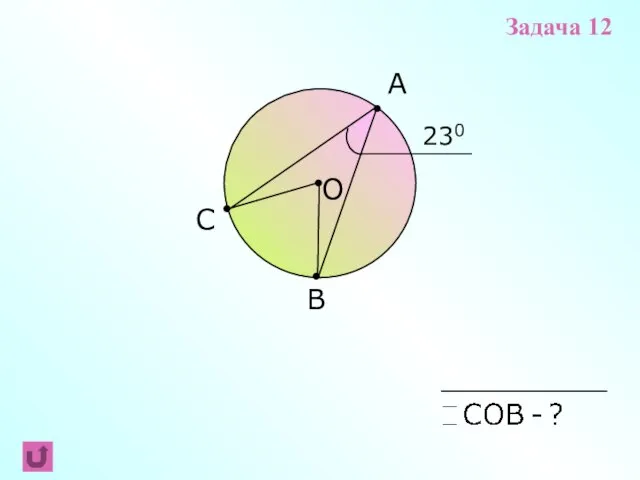
A
В
О
С
230
Задача 12

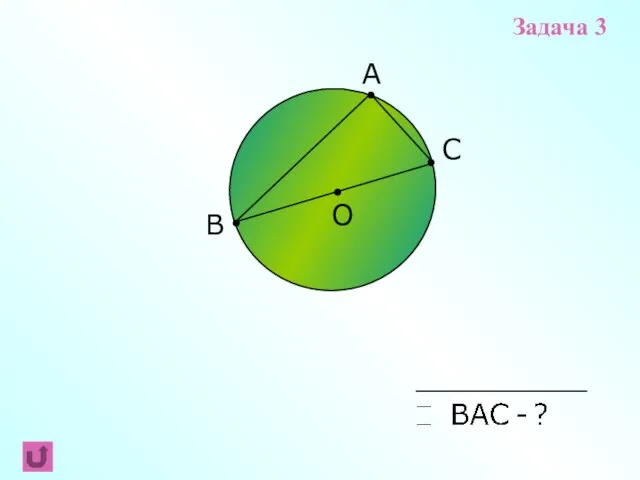
B
C
A
О
Задача 3

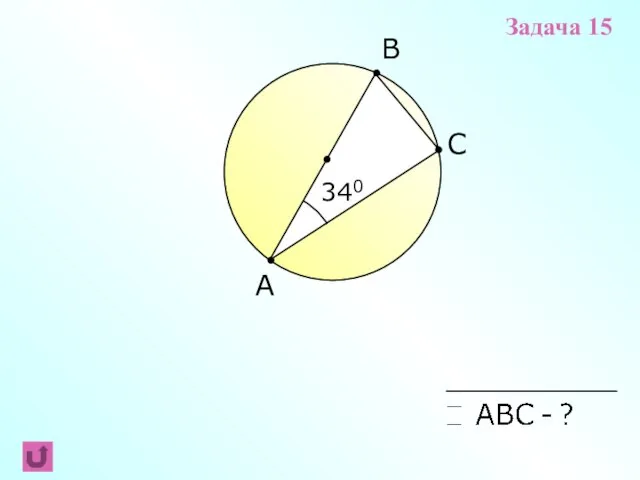
A
B
C
340
Задача 15

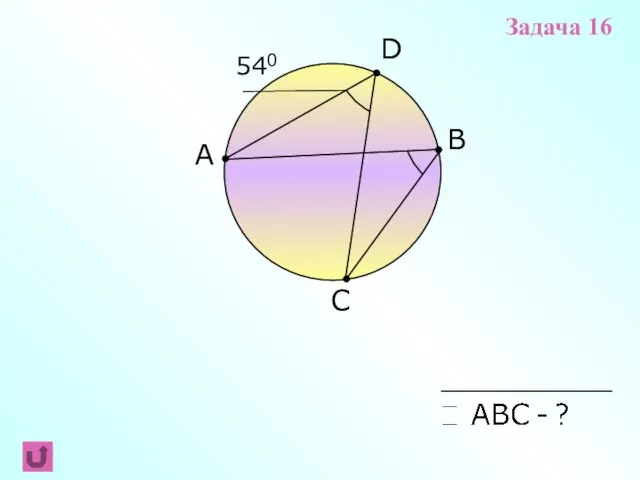
A
B
C
540
D
Задача 16

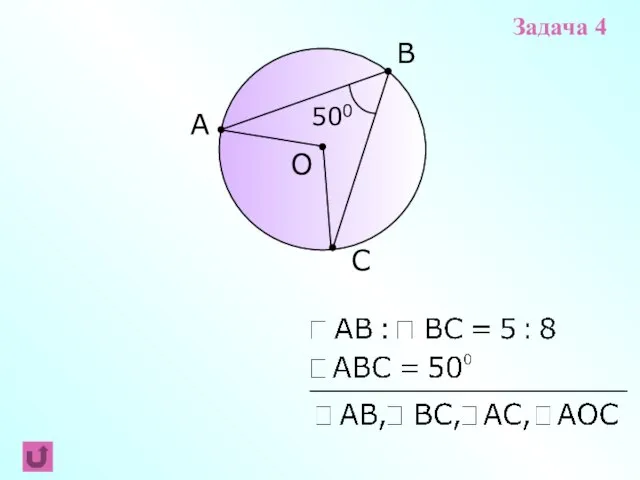
B
C
A
O
500
Задача 4

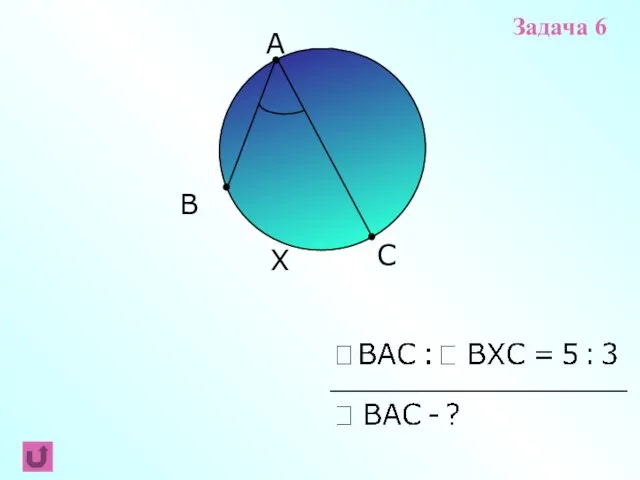
B
C
A
X
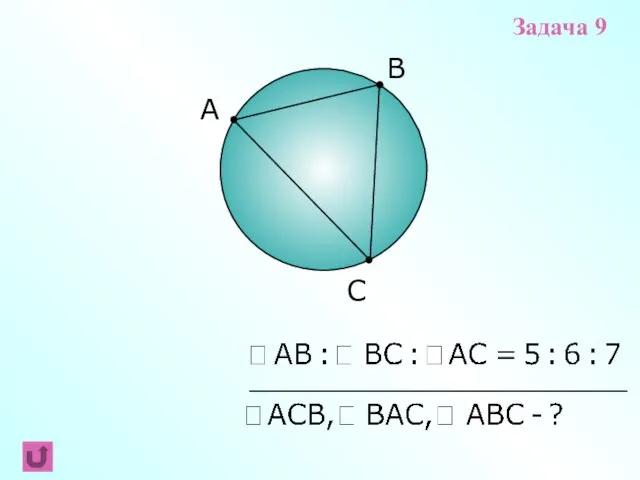
Задача 6

B
C
Задача 9

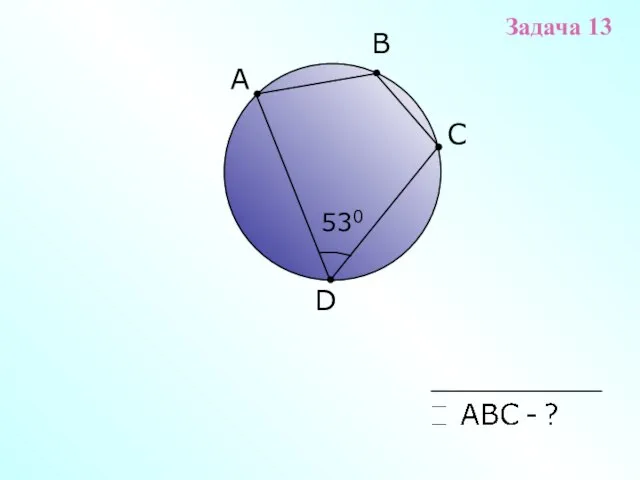
A
B
D
C
530
Задача 13

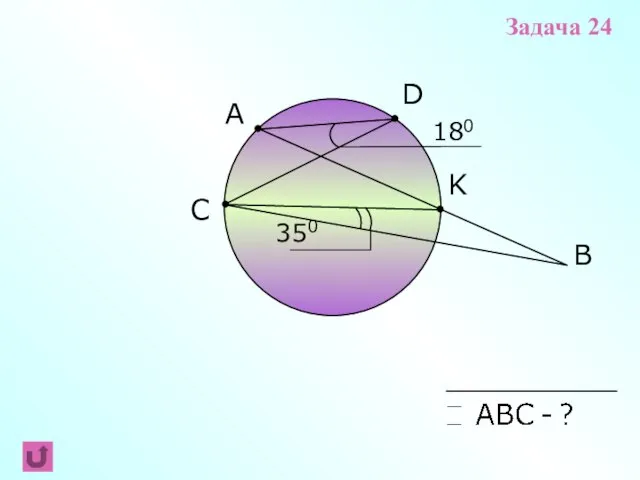
A
B
C
D
180
350
K
Задача 24

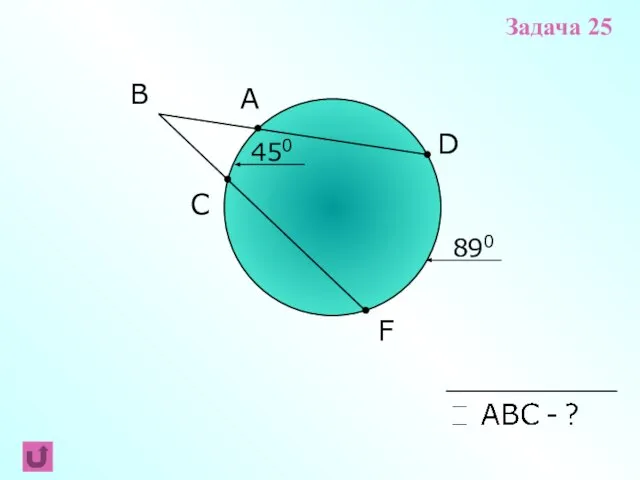
F
B
C
A
450
D
890
Задача 25

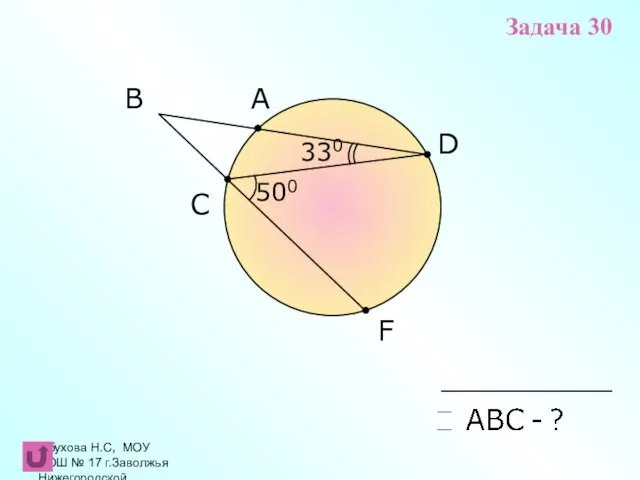
Обухова Н.С, МОУ СОШ № 17 г.Заволжья Нижегородской области
F
B
C
A
330
D
500
Задача 30