Слайд 2Определение
Линейной функцией называется функция, задаваемая формулой вида:
y = kx + b,

где k и b - некоторые числа.
Слайд 3Прямопропорциональная зависимость
Зависимость между переменными x и y в линейной функции y

= kx является прямопропорциональной.
Слайд 4Свойства линейной функции y = kx при k ≠0
Область определения функции –

множество R всех действительных чисел.
Корни - единственный корень x = 0.
Промежутки постоянного знака зависят от знака параметра k:
k > 0, то y > 0 при x > 0 ; y < 0 при x < 0;
k < 0, то y > 0 при x < 0 ; y < 0 при x > 0.
Экстремумов нет.
Слайд 5Монотонность функции:
если k > 0, то y возрастает на всей числовой

оси;
если k < 0, то y убывает на всей числовой оси.
Наибольшего и наименьшего значений нет.
Область значений - множество R.
Четность - функция y = kx нечетная.
Слайд 6График линейной функции
y = kx
Графиком линейной функции y = kx является

прямая, проходящая через начало координат.
Коэффициент k называется угловым коэффициентом этой прямой.
Он равен тангенсу угла наклона этой прямой к оси X: k = tgα.
При положительных k этот угол острый, при отрицательных - тупой.
Слайд 7График линейной функции
y = kx+b
Графиком линейной функции y = kx +

b является прямая, смещенная на b единиц.
Для построения графика достаточно двух точек.
Например: A(0;b) B(−kb;0), если k ≠0 .
Слайд 8Общий случай
График линейной функции y = kx + b при k ≠0, b
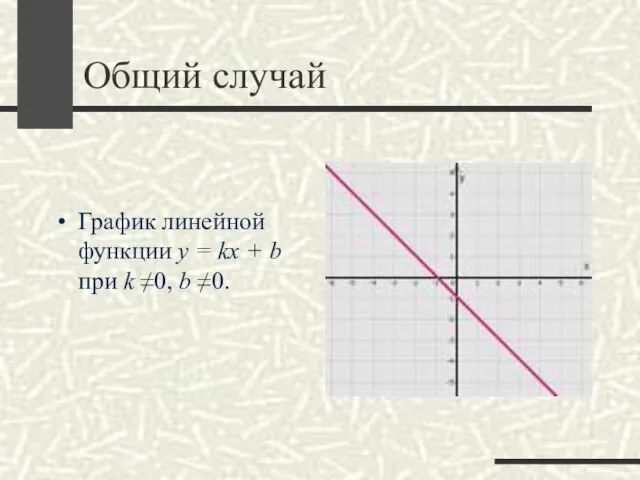
≠0.
Слайд 9Частный случай: b =0
График линейной функции y = kx + b при
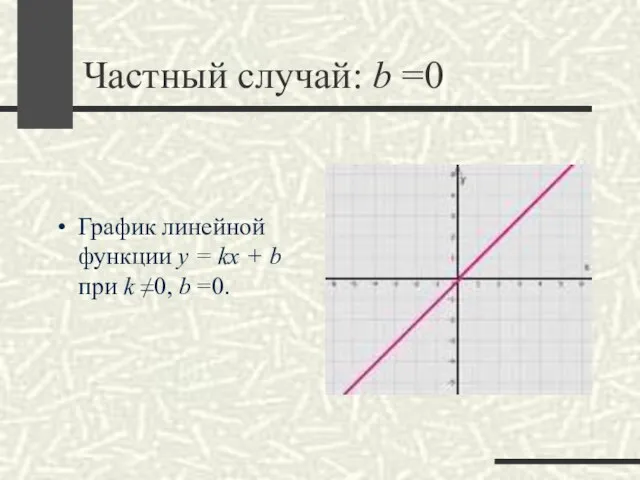
k ≠0, b =0.
Слайд 10Частный случай: k =0
График линейной функции y = kx + b при
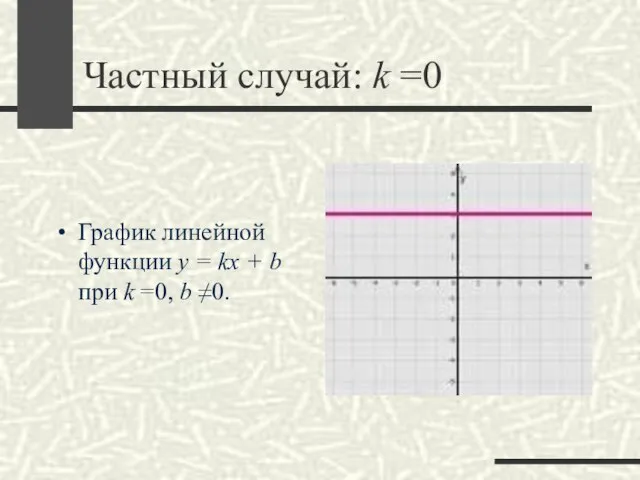
k =0, b ≠0.









 Маркетинговое планирование
Маркетинговое планирование Психологическая подготовка к всероссийской олимпиаде профессионального мастерства. 2021г
Психологическая подготовка к всероссийской олимпиаде профессионального мастерства. 2021г ЗНАЧЕНИЕ МИРОВОГО ОКЕАНА В ЖИЗНИ ЛЮДЕЙ
ЗНАЧЕНИЕ МИРОВОГО ОКЕАНА В ЖИЗНИ ЛЮДЕЙ Ночь искусств. Театр как вид искусства
Ночь искусств. Театр как вид искусства Герои Чернушки
Герои Чернушки Фотография авангарда
Фотография авангарда Здоровье – ни с чем не сравнимая ценность. 5 класс
Здоровье – ни с чем не сравнимая ценность. 5 класс На востоке встаёт луна, На западе гаснет солнце, А ветка вишни моей цветёт. Суворова Альбина 8 класс, школа 541
На востоке встаёт луна, На западе гаснет солнце, А ветка вишни моей цветёт. Суворова Альбина 8 класс, школа 541 Юные герои Первой мировой войны
Юные герои Первой мировой войны Методика проведения международных маркетинговых исследований Дисциплина: Международный маркетинг Преподаватель: профессор ка
Методика проведения международных маркетинговых исследований Дисциплина: Международный маркетинг Преподаватель: профессор ка Презентация на тему Скульптура Древнего Рима
Презентация на тему Скульптура Древнего Рима  Переобучение, повышение квалификации женщин, находящихся в отпуске по уходу за ребенком
Переобучение, повышение квалификации женщин, находящихся в отпуске по уходу за ребенком Международно-правовое регулирование охраны труда
Международно-правовое регулирование охраны труда Бандажна проходка
Бандажна проходка Дмитрий Иванович Мендилеев
Дмитрий Иванович Мендилеев Персоналии в отечественной социальной психологии
Персоналии в отечественной социальной психологии Презентация на тему Презентации Омар Хайям
Презентация на тему Презентации Омар Хайям Тепло из недр Земли
Тепло из недр Земли Успешный опыт использования поисковой интернет- рекламы в продажах садовой техники - ООО «Садторг» (www.dom-sad.ru, www.tehnosad.ru)www.dom-sad.ruwww.tehnos
Успешный опыт использования поисковой интернет- рекламы в продажах садовой техники - ООО «Садторг» (www.dom-sad.ru, www.tehnosad.ru)www.dom-sad.ruwww.tehnos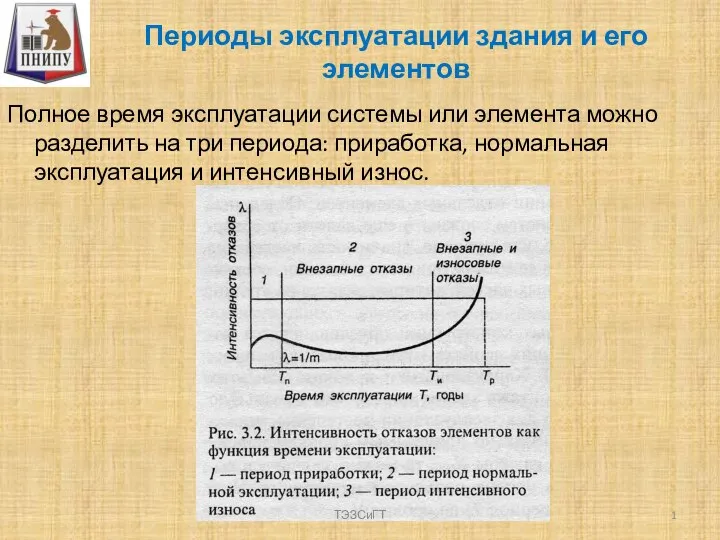 Периоды эксплуатации здания и его элементов
Периоды эксплуатации здания и его элементов Подборка телерекламы из Интернета по объекту рекламирования
Подборка телерекламы из Интернета по объекту рекламирования Когнитивные особенности младенца
Когнитивные особенности младенца Практика защиты авторских прав для произведений в интернете
Практика защиты авторских прав для произведений в интернете Презентация на тему Водные ресурсы мира (10 класс)
Презентация на тему Водные ресурсы мира (10 класс) Работа выполнена в рамках проекта «Повышение квалификаций различных категорий работников образования и формирование у них базов
Работа выполнена в рамках проекта «Повышение квалификаций различных категорий работников образования и формирование у них базов Компьютерный дизайн как профессия
Компьютерный дизайн как профессия БАСНИ- «КНИГА МУДРОСТИ САМОГО НАРОДА» (Н.В.ГОГОЛЬ)
БАСНИ- «КНИГА МУДРОСТИ САМОГО НАРОДА» (Н.В.ГОГОЛЬ) Производитель комплектующих для промышленной вентиляции
Производитель комплектующих для промышленной вентиляции