Линейная парная регрессия

Уравнение линейной парной регрессии имеет вид:
Коэффициент b – коэффициент регрессии
Он показывает среднее изменение показателя у с изменением фактора х на единицу

Уравнение линейной парной регрессии:
Необходимо оценить (найти) параметры уравнения: а и b.

Метод наименьших квадратов
Минимизируется сумма квадратов отклонений фактических значений переменной от теоретических

Метод наименьших квадратов
Задача сводится к решению системы нормальных уравнений
Выкладки на доске

Метод наименьших квадратов
Преобразуя систему уравнений, получаем:
Выкладки на доске

Метод наименьших квадратов
Решая систему находим параметры модели:
Выкладки на доске

Как количественно оценить линейную связь между переменными?
с помощью линейного коэффициента корреляции:

Коэффициент корреляции
связан с коэффициентом регрессии:
Так как

Свойства линейного коэффициента корреляции:

Примерные задания для самостоятельной работы
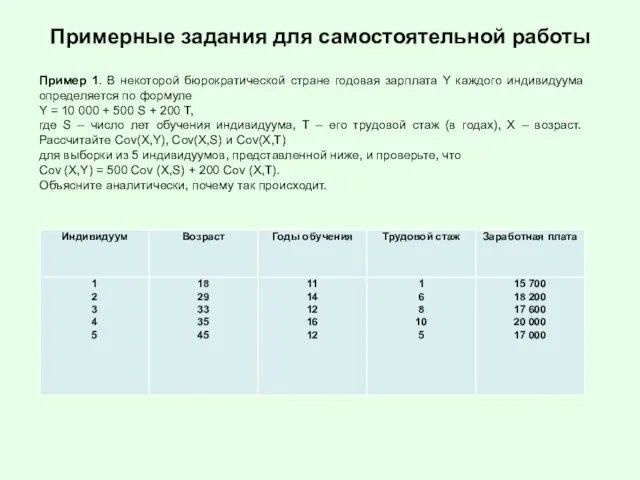
Пример 1. В некоторой бюрократической стране годовая зарплата Y каждого индивидуума определяется по формуле
Y = 10 000 + 500 S + 200 T,
где S – число лет обучения индивидуума, Т – его трудовой стаж (в годах), X – возраст. Рассчитайте Cov(X,Y), Cov(X,S) и Cov(X,T)
для выборки из 5 индивидуумов, представленной ниже, и проверьте, что
Cov (X,Y) = 500 Cov (X,S) + 200 Cov (X,T).
Объясните аналитически, почему так происходит.