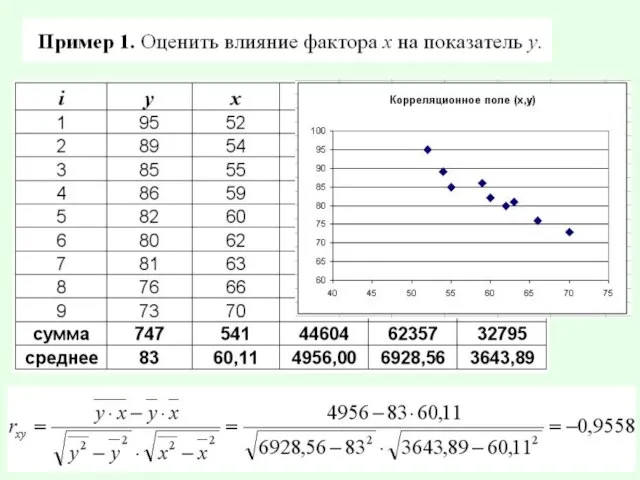
Слайд 2Рассмотрим зависимость между ценой (х) и спросом (у). Данные наблюдений изобразим точками
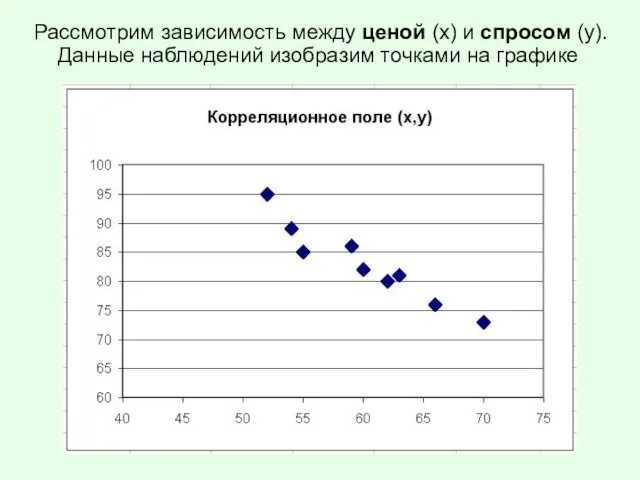
на графике
Слайд 3На графике видно, что между величинами есть сильная линейная связь
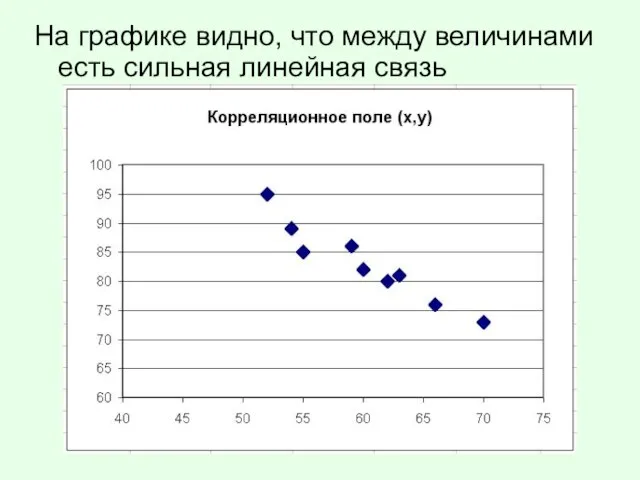
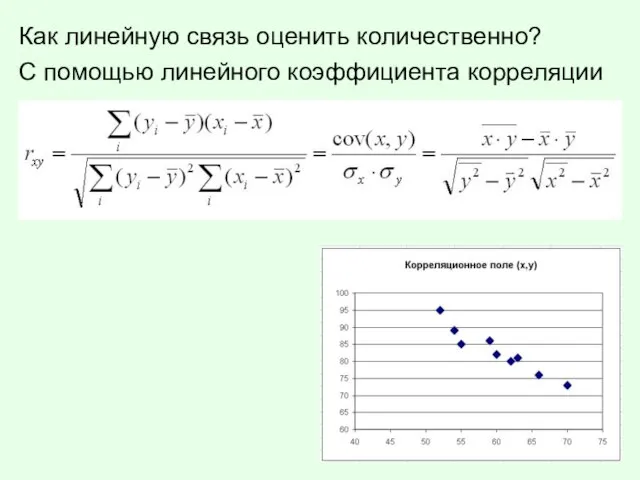
Слайд 4Как линейную связь оценить количественно?
С помощью линейного коэффициента корреляции
Слайд 5Свойства линейного коэффициента корреляции:

Слайд 6Различные графики распределений пар (x,y) с коэффициентами корреляции

Слайд 7Коэффициент корреляции отражает линейную зависимость (верхняя строка)

Слайд 8но не описывает кривую зависимости (средняя строка)

Слайд 9и совсем не подходит для описания сложных, нелинейных зависимостей (нижняя строка)

Слайд 10Корреляция между переменными может оказаться ложной.
Например, из-за наличия у них трендов
Тренд –

длительная тенденция изменения экономических показателей
Слайд 11Для выявления ложной корреляции можно измерить корреляцию не самих показателей х и

у, а их первых разностей Δх и Δу.
Слайд 13Большое значение коэффициента корреляции говорит о сильной обратной линейной связи между рассматриваемыми
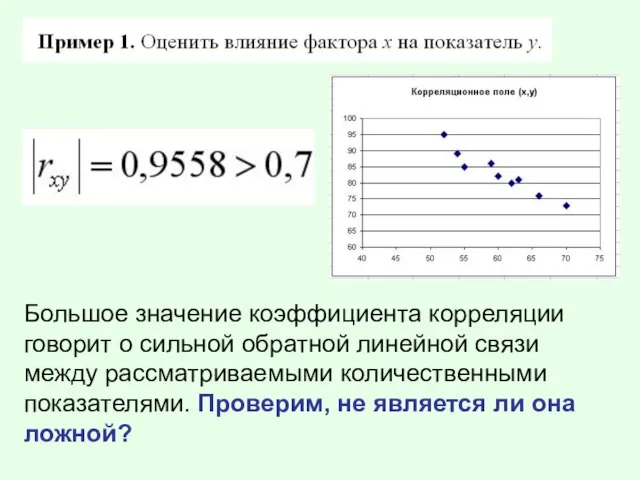
количественными показателями. Проверим, не является ли она ложной?
Слайд 14Проверим, является ли корреляция ложной?
Найдем корреляцию между первыми разностями
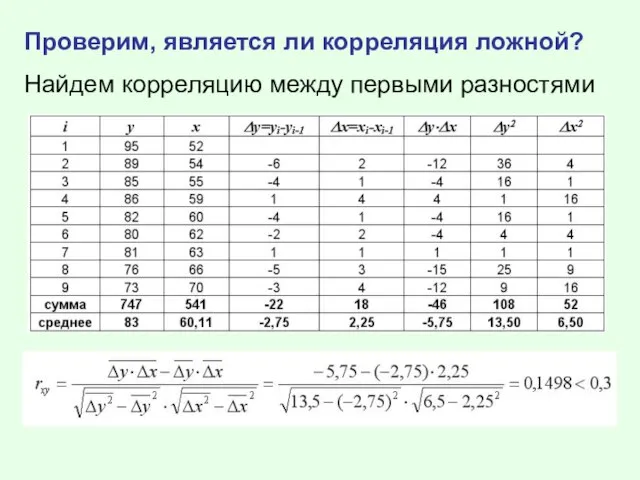
Слайд 15Корреляция между первыми разностями
Получили маленькое значение, следовательно, сильная линейная связь между показателями
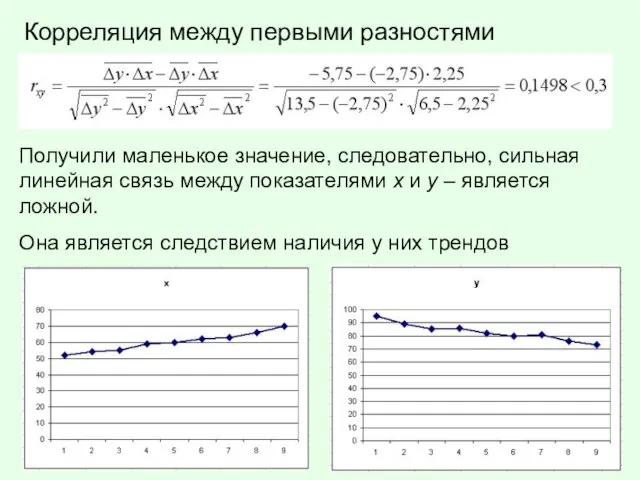
х и у – является ложной.
Она является следствием наличия у них трендов
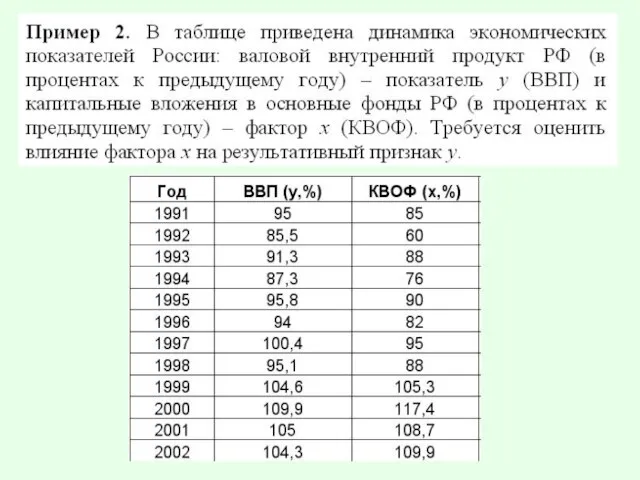
Слайд 17Рассчитаем коэффициент корреляции между переменными
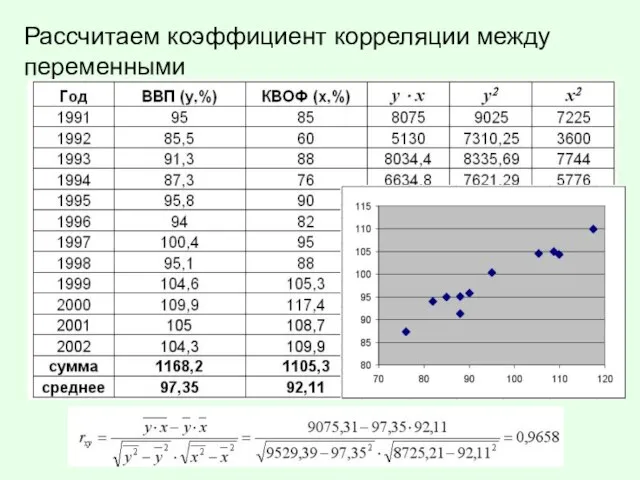
Слайд 18Следовательно имеет место сильная прямая линейная связь между темпом роста валового внутреннего

продукта РФ (ВВП) и темпом роста капитальных вложений в основные фонды РФ (КВОФ).
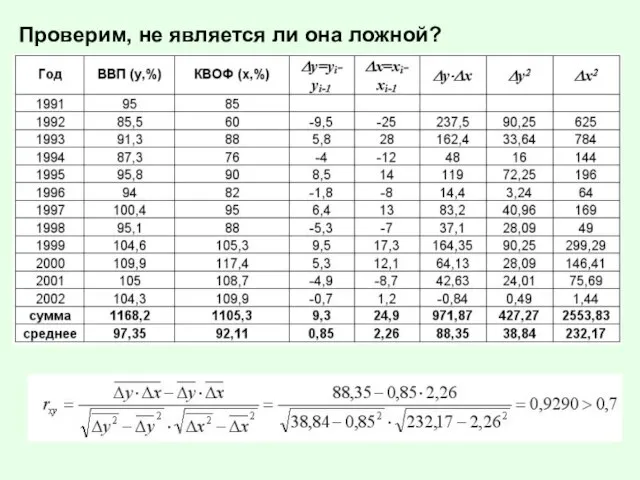
Проверим, не является ли она ложной?
Слайд 19Проверим, не является ли она ложной?
















 Показатели качества деталей. Классификация показателей качества продукции. Определение номеклатуры показателей качества
Показатели качества деталей. Классификация показателей качества продукции. Определение номеклатуры показателей качества Кожа и ультрафиолетовые лучи
Кожа и ультрафиолетовые лучи Принципы, критерии и методы педагогического прогнозирования индивидуальной образовательной траектории
Принципы, критерии и методы педагогического прогнозирования индивидуальной образовательной траектории Студенческое самоуправление:основные мероприятия в 2011 г.
Студенческое самоуправление:основные мероприятия в 2011 г. Игры со шнуровкой
Игры со шнуровкой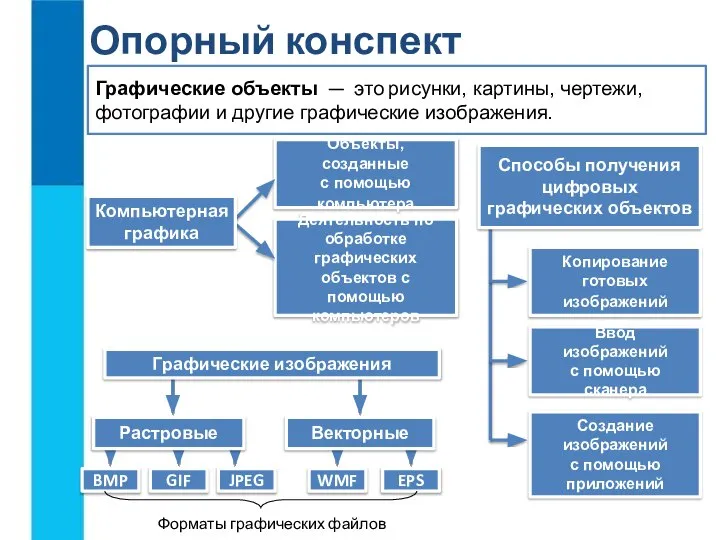 Графические объекты. Опорный конспект
Графические объекты. Опорный конспект Жизнь экосистемы. Биосфера и экосистема. Экологическая система
Жизнь экосистемы. Биосфера и экосистема. Экологическая система Руководство механики работы по проекту AUTO.RU
Руководство механики работы по проекту AUTO.RU Особенности энергосервисных контрактов в многоквартирных домах
Особенности энергосервисных контрактов в многоквартирных домах Презентация на тему Умножение и деление положительных и отрицательных чисел
Презентация на тему Умножение и деление положительных и отрицательных чисел Популяция (1)
Популяция (1) Конкурсный проект смотровой площадки на вершине горы Машук
Конкурсный проект смотровой площадки на вершине горы Машук Презентация на тему Рокоссовский Константин Константинович
Презентация на тему Рокоссовский Константин Константинович  Радианная мера углов и дуг
Радианная мера углов и дуг ДИАГРАММА «Моя квартира»
ДИАГРАММА «Моя квартира» Инфекционные осложнения после абортов
Инфекционные осложнения после абортов Гонка Чемпионов: Шумахер или Лёб? Тактика выживания бизнеса в кризис Сергей Петренко 1 апреля 2009 года. - презентация
Гонка Чемпионов: Шумахер или Лёб? Тактика выживания бизнеса в кризис Сергей Петренко 1 апреля 2009 года. - презентация Сведения о бетоне
Сведения о бетоне Право и государство
Право и государство За счет чего российские компании могут конкурировать глобально?
За счет чего российские компании могут конкурировать глобально? Cистема FATC1 климат-контроль
Cистема FATC1 климат-контроль "АНТИКРИЗИСНОЕ УПРАВЛЕНИЕ"
"АНТИКРИЗИСНОЕ УПРАВЛЕНИЕ" Александр Невский (7 класс)
Александр Невский (7 класс) Фонд обязательного медицинского страхования
Фонд обязательного медицинского страхования Ясенев Вячеслав Николаевич
Ясенев Вячеслав Николаевич Летний оздоровительный лагерь «МАЛЫШОК»
Летний оздоровительный лагерь «МАЛЫШОК» Программы сопровождения педагогических кадров Профессионал
Программы сопровождения педагогических кадров Профессионал Презентация на тему Антикоррупционная политика
Презентация на тему Антикоррупционная политика