Содержание
- 2. СЕДЬМОЕ МАТЕМАТИЧЕСКОЕ ДЕЙСТВИЕ Алгебру называют нередко «арифметикой семи действий», подчеркивая, что к четырем общеизвестным математическим операциям
- 3. Дата рождения: 1550 год Место рождения: замок Мерчистон, в те годы предместье Эдинбурга Научная сфера: математика
- 4. Для чего были придуманы логарифмы? Конечно, для ускорения и упрощения вычислений. Изобретатель первых логарифмических таблиц, Непер,
- 5. УСТНАЯ РАБОТА
- 6. ОПРЕДЕЛЕНИЕ ЛОГАРИФМА Логари́фмом положительного числа b по основанию a, где а>0, а≠1,называется показатель степени, в которую
- 7. ПРИ КАКИХ ЗНАЧЕНИЯХ Х СУЩЕСТВУЕТ ЛОГАРИФМ Х > 3 X X X R Не существует ни
- 8. СВОЙСТВА ЛОГАРИФМОВ ПУСТЬ С>0, C≠1, A>0,B>0, K-ЛЮБОЕ ЧИСЛО 1) Логарифм произведения logс( ab ) = logс
- 9. ЛОГАРИФМИЧЕСКАЯ ФУНКЦИЯ где а – заданное число, а>0, a≠1 , Т.к. логарифм – это показатель степени,
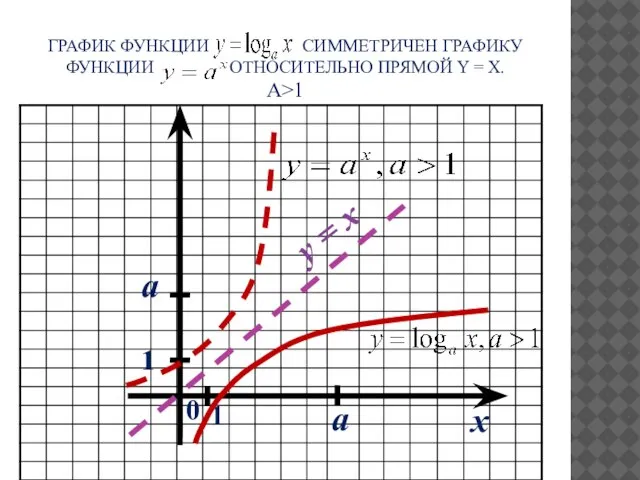
- 10. ГРАФИК ФУНКЦИИ СИММЕТРИЧЕН ГРАФИКУ ФУНКЦИИ ОТНОСИТЕЛЬНО ПРЯМОЙ Y = X. А>1 x 0 a a y
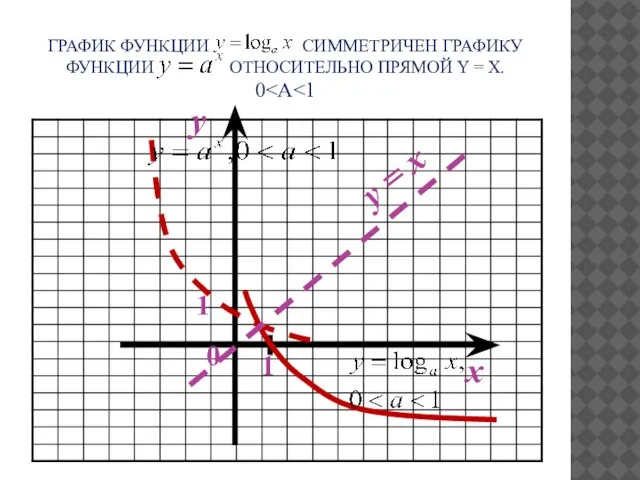
- 11. ГРАФИК ФУНКЦИИ СИММЕТРИЧЕН ГРАФИКУ ФУНКЦИИ ОТНОСИТЕЛЬНО ПРЯМОЙ Y = X. 0 x y y = x
- 12. СВОЙСТВА ЛОГАРИФМИЧЕСКОЙ ФУНКЦИИ 1. Область определения - множество всех положительных чисел 2. Множество значений – множество
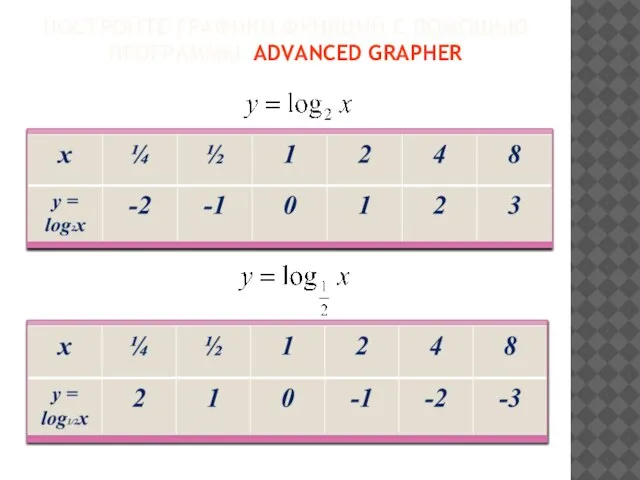
- 13. ПОСТРОЙТЕ ГРАФИКИ ФУНКЦИЙ С ПОМОЩЬЮ ПРОГРАММЫ ADVANCED GRAPHER
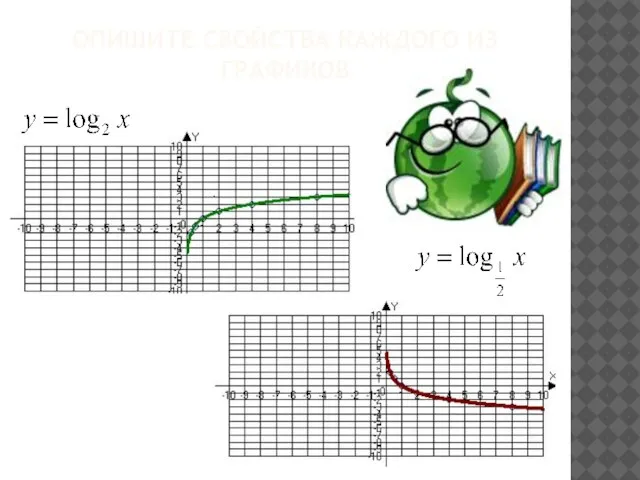
- 14. ОПИШИТЕ СВОЙСТВА КАЖДОГО ИЗ ГРАФИКОВ
- 15. ПОСТРОЙТЕ С ПОМОЩЬЮ ПРОГРАММЫ ADVANCED GRAPHER ГРАФИКИ ФУНКЦИЙ
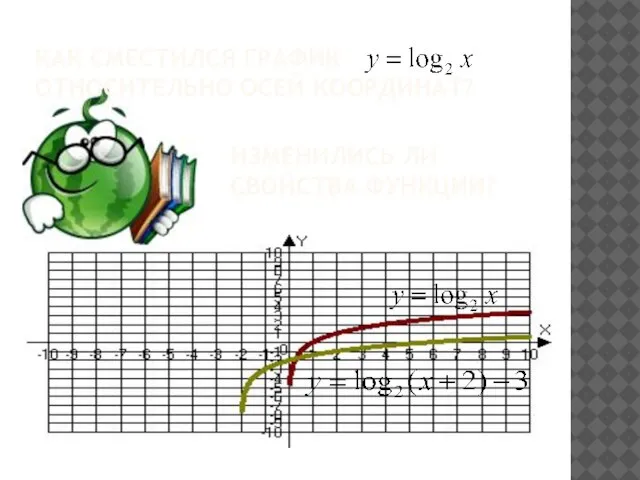
- 16. КАК СМЕСТИЛСЯ ГРАФИК ОТНОСИТЕЛЬНО ОСЕЙ КООРДИНАТ? ИЗМЕНИЛИСЬ ЛИ СВОЙСТВА ФУНКЦИИ?
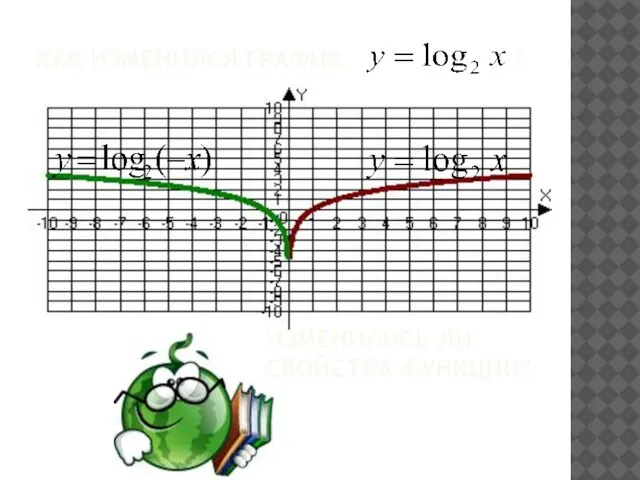
- 17. КАК ИЗМЕНИЛСЯ ГРАФИК ? ИЗМЕНИЛИСЬ ЛИ СВОЙСТВА ФУНКЦИИ?
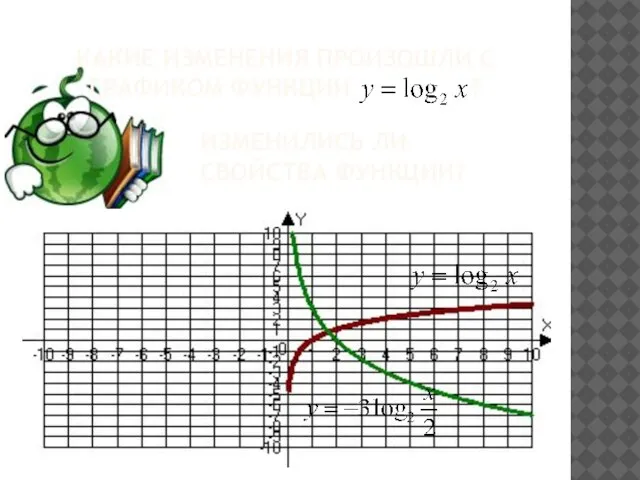
- 18. КАКИЕ ИЗМЕНЕНИЯ ПРОИЗОШЛИ С ГРАФИКОМ ФУНКЦИИ ? ИЗМЕНИЛИСЬ ЛИ СВОЙСТВА ФУНКЦИИ?
- 19. САМОСТОЯТЕЛЬНАЯ РАБОТА
- 20. Подведение итогов урока Дайте определение логарифмической функции Опишите свойства логарифмической функции Проведите сравнительный анализ графиков логарифмической
- 21. Домашнее задание Создание презентации по теме «Логарифмы»
- 23. Скачать презентацию













 THE CHRISTIAN WORKER
THE CHRISTIAN WORKER 1665678763032__30ro86
1665678763032__30ro86 Агрессия (4 класс)
Агрессия (4 класс) 1.1 + 1.2
1.1 + 1.2 История носового платка
История носового платка Поля листа
Поля листа Вкусное и красивое лакомство для неожиданных гостей
Вкусное и красивое лакомство для неожиданных гостей Добро пожаловать
Добро пожаловать Независимое распределение затрат в управленческом и регламентированном учете
Независимое распределение затрат в управленческом и регламентированном учете Абсолютные показатели оценки риска
Абсолютные показатели оценки риска Кипение
Кипение Страны Северной Европы
Страны Северной Европы Конструкция головы человека и её пропорции (6 класс)
Конструкция головы человека и её пропорции (6 класс) Энтеровирусная инфекция
Энтеровирусная инфекция Конвекция
Конвекция САНИТАРНО-ЭПИДЕМИОЛОГИЧЕСКИЕ ТРЕБОВАНИЯ К УСЛОВИЯМИ ОРГАНИЗАЦИИ ОБУЧЕНИЯ В ОБЩЕОБРАЗОВАТЕЛЬНЫХ УЧРЕЖДЕНИЯХ
САНИТАРНО-ЭПИДЕМИОЛОГИЧЕСКИЕ ТРЕБОВАНИЯ К УСЛОВИЯМИ ОРГАНИЗАЦИИ ОБУЧЕНИЯ В ОБЩЕОБРАЗОВАТЕЛЬНЫХ УЧРЕЖДЕНИЯХ Ассоциация «МЫ»
Ассоциация «МЫ»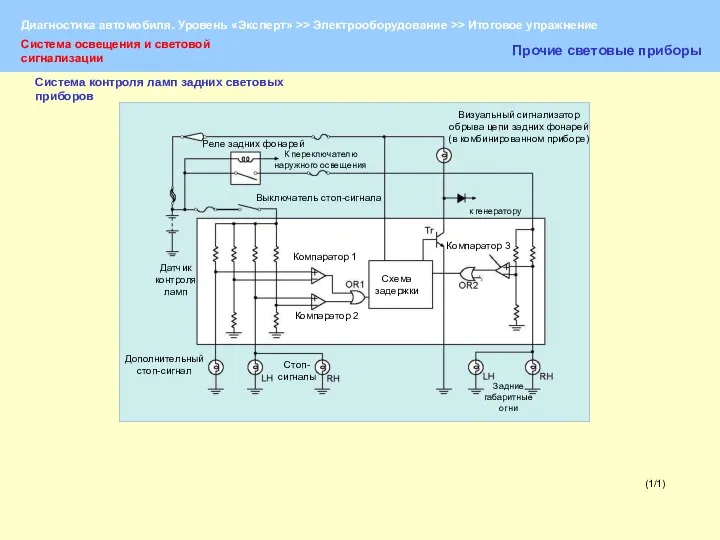 Диагностика автомобиля. Диагностирование осветительных приборов
Диагностика автомобиля. Диагностирование осветительных приборов Денис Васильевич Давыдов
Денис Васильевич Давыдов Рекомендую как пособие по медицинской генетике
Рекомендую как пособие по медицинской генетике Любимый семейный завтрак семьи Пьянковых
Любимый семейный завтрак семьи Пьянковых Доброта
Доброта О РЕЗУЛЬТАТАХ ЕГЭ в г. Сочи в 2011 ГОДУ
О РЕЗУЛЬТАТАХ ЕГЭ в г. Сочи в 2011 ГОДУ Психологические закономерности формирования личности в тренировочном процессе.
Психологические закономерности формирования личности в тренировочном процессе. Базовый межшкольный методический центр 26311
Базовый межшкольный методический центр 26311 Сложение и вычитание двузначных чисел 2 класс
Сложение и вычитание двузначных чисел 2 класс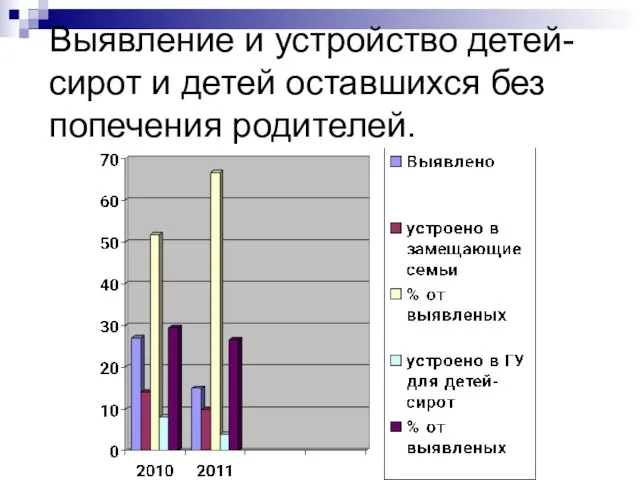 Выявление и устройство детей-сирот и детей оставшихся без попечения родителей.
Выявление и устройство детей-сирот и детей оставшихся без попечения родителей. Создание единого китайского государства
Создание единого китайского государства