Логарифмы

Повторить и закрепить:
свойства логарифма и логарифмической функции;
способы решения логарифмических уравнений и неравенств;
навыки и умения применения знаний по теме к решению упражнений.
Задачи урока:

Основные умения

Этапы урока. Форма работы.
Воспроизведение и коррекция опорных знаний. Фронтальная
Применение знаний для объяснения новых фактов и выполнения практических заданий. Работа в парах
Тест. Индивидуальная
Подведение итогов урока

Определение логарифма
Логарифмом положительного числа b по положительному и отличному от 1 основанию а называют показатель степени, в которую нужно возвести число а, чтобы получить число b.
Основное логарифмическое тождество

Свойства логарифмов

Свойства монотонности логарифмов
Если a > 1 и b > c, то
Если 0 < a < 1 и b > c, то

Десятичные логарифмы
Если основание логарифма равно 10, то логарифм называется десятичным:
Натуральные логарифмы
Если основание логарифма е, то логарифм называется натуральным:

Логарифмирование
алгебраических выражений
Если число х представлено алгебраическим выражением, то логарифм любого выражения можно выразить через логарифмы составляющих его чисел.
Прологарифмировать алгебраическое выражение:

Потенцирование
логарифмических выражений
Переход от логарифмического выражения к алгебраическому называется потенцированием, то есть, произвести действие, обратное логарифмированию
Перейти к алгебраическому выражению

При каких значениях х имеет смысл функция:
Устные упражнения
Совпадают ли графики функций:
Решить уравнение:

Задание с ключом.
1) Если lg x = lg y, то x = y.
Ключ: 101000100.

Найти х:
lg x = lg a + 2lg b – lg c
lg x = lg d + 3lg c – 4lg b
lg x = lg 5 - lg 2 + lg 6
lg x = 2lg 3 + 3lg 5 – 5lg 3
Прологарифмировать алгебраическое выражение:
lg x = lg a + 2lg b – 3lg c
lg x = 2lg m + 3lg n – 2lg t
lg x = 2lg m - 4lg n – 5lg k

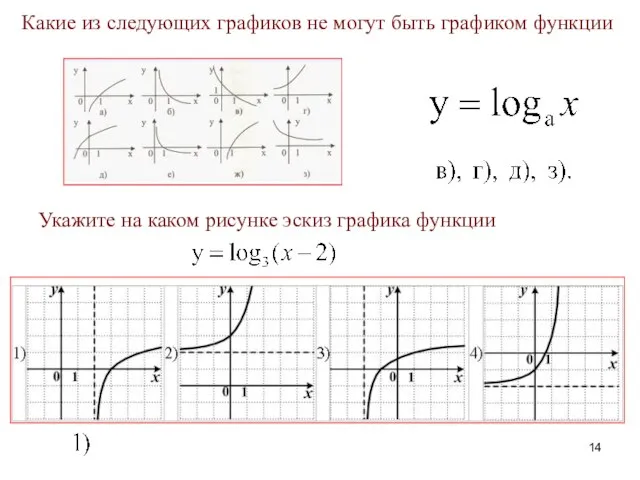
Укажите на каком рисунке эскиз графика функции
Какие из следующих графиков не могут быть графиком функции

Основные методы решения логарифмических уравнений
Функционально-графический метод;
Метод потенцирования;
Метод введения новой переменной;
Метод логарифмирования.

Решить уравнение
х =1; х = 2.
Найти область определения функции
(-2;-1]; [1; + ∞)
Решите систему уравнений
Найдите наименьшее значение функции