Содержание
- 2. Logica poate fi definită ca știință a evaluării argumentelor(raționamentelor). Un argument în logică, este un șir
- 3. În literatura de specialitate deseori este utilizează sinonimul “logica formală”. Logica este o știință formală întrucât
- 4. Se numește propoziție un enunț al limbajului natural sau al unui limbaj simbolic despre care se
- 5. Este foarte important a observa că fiecare propoziție este adevărată sau falsă în raport cu o
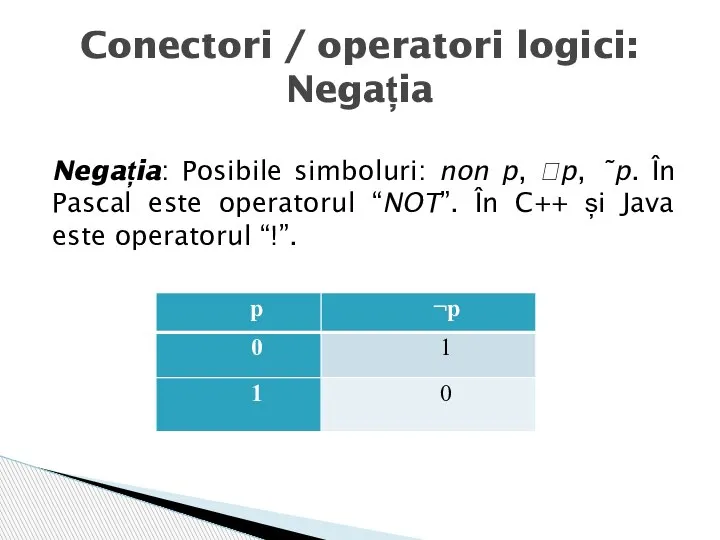
- 6. Negația: Posibile simboluri: non p, p, ˜p. În Pascal este operatorul “NOT”. În C++ și Java
- 7. Conjuncția: Posibile simboluri: p AND q, p&q. În Pascal este operatorul “AND”. În C++ și Java
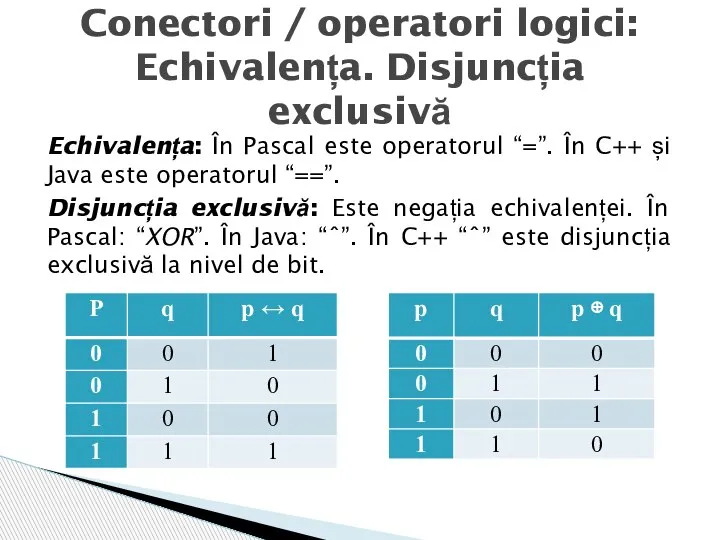
- 8. Echivalența: În Pascal este operatorul “=”. În C++ și Java este operatorul “==”. Disjuncția exclusivă: Este
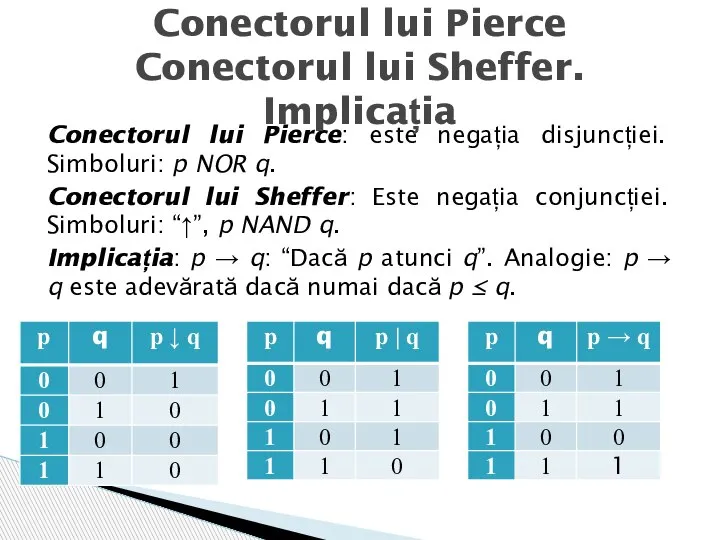
- 9. Conectorul lui Pierce: este negația disjuncției. Simboluri: p NOR q. Conectorul lui Sheffer: Este negația conjuncției.
- 10. Implicația este mai puțin intuitiva decât ceilalți conectori logici. Să considerăm două calculatoare, A și B,
- 11. Implicația (p → q) constă din premisă şi concluzie. Concluzia se mai numeşte condiție necesară pentru
- 12. Conectori logici în cadrul limbajului natural Ierarhia conectorilor logici. Lista conectorilor logici în ordinea descreşterii priorității:
- 13. Negație corectă: X nu este tânăr și frumos. Negație incorectă: X este bătrân și urât. Negație
- 14. Filtrarea rezultatelor căutărilor (Google, MS Access, SQL etc.); Expresii logice în algoritmi. Aplicații ale conectorilor logici
- 15. Orice propoziție obținută din alte propoziții prin intermediul conectorilor logici se numeşte formulă propozițională. Ramura logicii
- 16. Comutativitatea: p ∧ q ≡ q ∧ p; p ∨ q ≡ q ∨ p Asociativitatea:
- 17. Un număr impar de negații se reduce la o singură negație. Respectiv întreaga expresie “Aurel ...
- 18. Rezolvarea problemei logice “Două auditorii” p: “În primul auditoriu se află Cabinetul de Informatică”; q: “În
- 20. Скачать презентацию














 Основные понятия и законы динамики
Основные понятия и законы динамики Социальные эффекты информатизации
Социальные эффекты информатизации Михаил ЕвграфовичСалтыков-Щедрин
Михаил ЕвграфовичСалтыков-Щедрин Отдел мониторинга реализации стратегии развития университета и современных образовательных технологийСЕМИНАР-ТРЕНИНГ 2011 «Вне
Отдел мониторинга реализации стратегии развития университета и современных образовательных технологийСЕМИНАР-ТРЕНИНГ 2011 «Вне Уголовная ответственность несовершенолетних за кражи
Уголовная ответственность несовершенолетних за кражи Сибирское здоровье. Бизнес-план аптеки
Сибирское здоровье. Бизнес-план аптеки Dart
Dart Наши питомцы презентация
Наши питомцы презентация Презентация_8
Презентация_8 Проект фирмы Техсервис
Проект фирмы Техсервис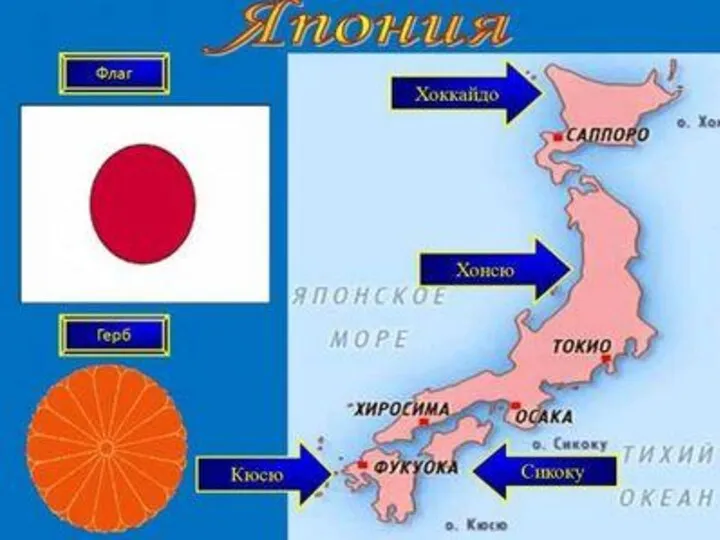 Япония
Япония О формировании Единого таможенного тарифа и мерах нетарифного регулирования в рамках Таможенного союза
О формировании Единого таможенного тарифа и мерах нетарифного регулирования в рамках Таможенного союза Презентация на тему Растения на гербах разных стран
Презентация на тему Растения на гербах разных стран Типичные налоговые претензии к малому и среднему бизнесу по спецрежимам, антикризисным льготам, увольнению персонала
Типичные налоговые претензии к малому и среднему бизнесу по спецрежимам, антикризисным льготам, увольнению персонала Высвобождение персонала
Высвобождение персонала XV-XVII ғасырлардағы қазақ әдеби тілінің үлгілері
XV-XVII ғасырлардағы қазақ әдеби тілінің үлгілері START UP
START UP Древня Русь (4 класс)
Древня Русь (4 класс) Просвещение
Просвещение Презентация на тему Вильгельм I Оранский
Презентация на тему Вильгельм I Оранский Инвестиционная безопасность РФ
Инвестиционная безопасность РФ Этюд Осеннее дерево
Этюд Осеннее дерево Организационная структура ТЭК ООО «Арго»
Организационная структура ТЭК ООО «Арго» Первая помощь при бытовых ожогах
Первая помощь при бытовых ожогах Работа с окнами в Windows
Работа с окнами в Windows Выборы-2001
Выборы-2001 Урок презентация на тему Откуда на небе облака
Урок презентация на тему Откуда на небе облака  Почти круглый стол Макса Вебера
Почти круглый стол Макса Вебера