Логика. Решение экзаменационных задач

Немного теории…
Алгебра логики – это раздел математики, изучающий высказывания со стороны их логических значений истинности или ложности.
Высказывание – это повествовательное предложение, относительно которого можно сказать истинно оно или ложно.
Пример:
Москва – это столица России
Сейчас идет снег
Растения не выделяют кислород

Логические операции
Операция отрицания
2) Логическое умножение (конъюнкция)
3) Логическое сложение (дизъюнкция)

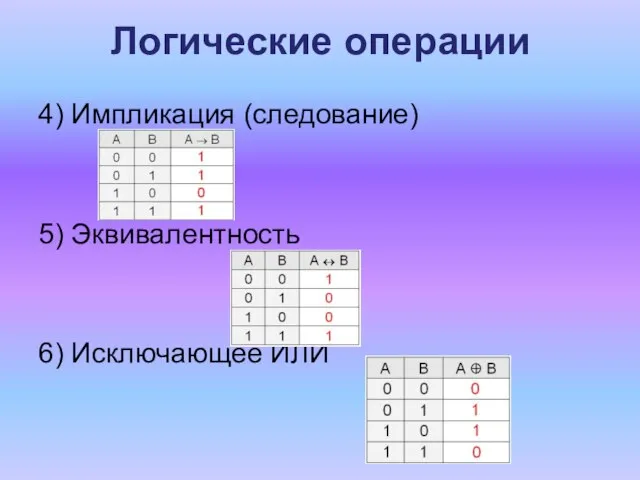
Логические операции
4) Импликация (следование)
5) Эквивалентность
6) Исключающее ИЛИ

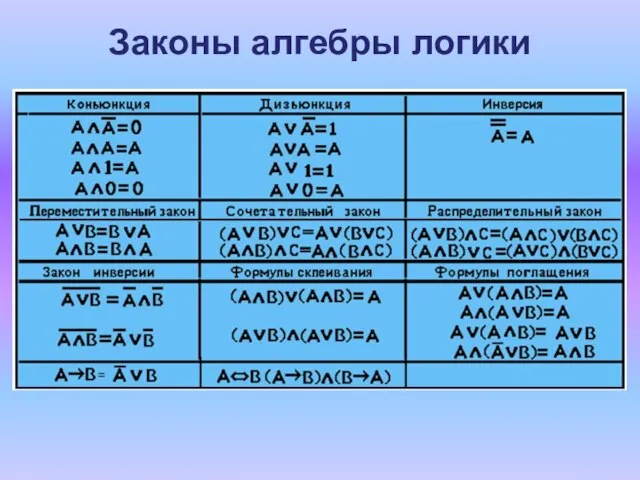
Законы алгебры логики

Решение задач

Задача №1
Для какого числа X истинно высказывание:
((x<4)→(x<3))^((x<3)→(x<1))
1)1 2)2 3)3 4)4
Решение:
Подставляем в выражение предложенные варианты ответа и определяем, истинно выражение или ложно:
1) x=1: ((1<4)→(1<3))^((1<3)→(1<1))=(1→1)^(1→0)
Сначала вычислим выражение в скобках:
(1→1)^(1→0)=1^0=0 (не подходит)
Аналогично подставляем другие варианты ответа, вычисляем:
2) x=2: ((2<4)→(2<3))^((2<3)→(2<1))=(1→1)^(1→0)=1^0=0 (не подходит)
3) x=3: ((3<4)→(3<3))^((3<3)→(3<1))=(1→0)^(0→0)=0^1=0 (не подходит)
4) x=4: ((4<4)→(4<3))^((4<3)→(4<1))=(0→0)^(0→0)=1^1=1 (подходит)
Ответ: 4.
задания

Задача №2
Для какого имени ложно высказывание:
(первая буква гласная ^последняя буква согласная)→ ¬(третья буква согласная)?
Дмитрий 2) Антон 3) Екатерина 4) Анатолий
Решение:
Подставляем в выражение предложенные варианты ответа и определяем, истинно выражение или ложно:
Дмитрий: (0 ^ 1)→ ¬(0)=0→1 = 1 (не подходит)
Антон: (1 ^ 1)→ ¬(1)=1→0 = 0 (подходит)
Екатерина: (1 ^ 0)→ ¬(0)=0→1 = 1 ( не подходит)
Анатолий: (1 ^ 1)→ ¬(0)=1→1 = 1 ( не подходит)
Ответ: 2.
задания

Задача №3
Построить таблицу истинности для следующей функции:
F(X,Y,Z)=(x→y)·z + ¬y
Решение:
1) Нарисуем таблицу на K строк, где K=2n, n - количество
высказываний в функции
N=3, k=8 строк
2) Запишем в таблице все варианты X,Y,Z и вычисляем выражение по
действиям:
задания

Задача №4
Символом F обозначено одно из указанных ниже
логических выражений от 3-х аргументов X,Y,Z. Дан
фрагмент таблицы истинности выражения F.
Какое выражение соответствует F?
Решение:
Подставляем значения X,Y,Z из таблицы в предложенные варианты ответа,
сравниваем со значением F(X,Y,Z):
Ответ: 4
задания

Задача №5
Какое логическое выражение равносильно выражению:
Решение: применим отрицание к выражению в скобках в соответствии с законом инверсии:
Ответ: 2.
задания

Задача №6
Каково наименьшее натуральное число X, при котором
истинно высказывание
Решение: Импликация ложна, когда первое выражение истинно, а второе ложно(см. таблицы истинности). Во всех остальных случаях импликация истинна. Первое выражение ложно для всех натуральных x>10 и истинно для всех натуральных x<11. Второе выражение истинно для всех натуральных x>9 и ложно для всех натуральных x<10. Следовательно, данная импликация истинна для всех натуральных x>9. Наименьшее число, соответствующее этому условию x=10.
Ответ: 10.
задания

Задача №7
Найдите все тройки значения L,M,N, при которых указанное выражение принимает ложное значение.
Решение:
Из таблицы истинности импликации получаем, что L=0, а
Подставляем полученное значение L в выражение в скобках:
Из таблицы истинности дизъюнкции следует,
что выражение истинно тогда и только тогда, когда
(M=1, N=0) или (M=0, N=1) или (M=1, N=1). Поскольку L=0,
ответом будут все тройки (L=0, M=1, N=0), (L=0, M=0, N=1),
(L=0,M=1, N=1).
Ответ: (L=0, M=1, N=0), (L=0, M=0, N=1), (L=0, M=1, N=1).
задания

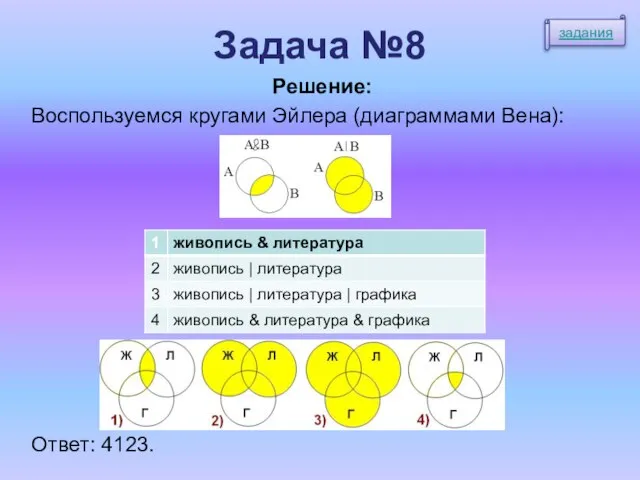
Задача №8
В таблице приведены запросы к поисковому серверу:
Расположите номера запросов в порядке возрастания количества страниц, которые найдёт поисковый сервер по каждому запросу.
Для обозначения логической операции «ИЛИ» в запросе используется символ |, а для логической операции «И» − &.

Задача №8
Решение:
Воспользуемся кругами Эйлера (диаграммами Вена):
Ответ: 4123.
задания

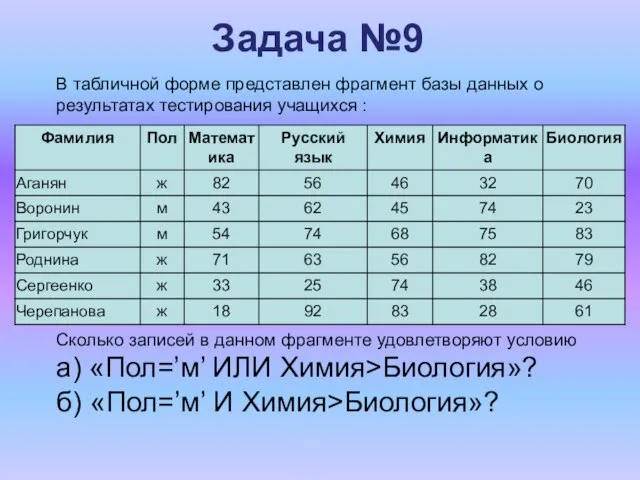
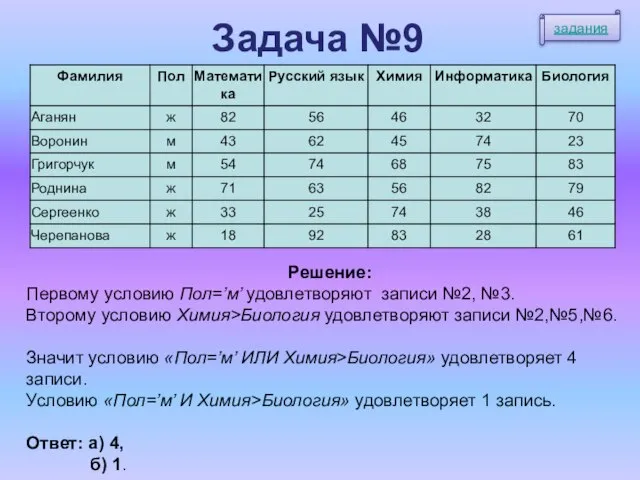
Задача №9
В табличной форме представлен фрагмент базы данных о результатах тестирования учащихся :
Сколько записей в данном фрагменте удовлетворяют условию
а) «Пол=’м’ ИЛИ Химия>Биология»?
б) «Пол=’м’ И Химия>Биология»?

Задача №9
Решение:
Первому условию Пол=’м’ удовлетворяют записи №2, №3.
Второму условию Химия>Биология удовлетворяют записи №2,№5,№6.
Значит условию «Пол=’м’ ИЛИ Химия>Биология» удовлетворяет 4 записи.
Условию «Пол=’м’ И Химия>Биология» удовлетворяет 1 запись.
Ответ: а) 4,
б) 1.
задания

Задания
1) Для какого числа X истинно высказывание:
1)1 2)3 3)4 4)2
2) Для какого числа X истинно высказывание:
1)1 2)2 3)3 4)4
3) Для какого числа X истинно высказывание:
1)1 2)2 3)3 4)4
4) Для какого числа X истинно высказывание:
1)1 2)2 3)3 4)4
5) Для какого числа X истинно высказывание:
1)1 2)2 3)3 4)4

Задания
1) Для какого имени истинно высказывание:
1) КСЕНИЯ 2) ЮЛИЯ 3) ПЕТР 4) АЛЕКСЕЙ
2) Для какого имени истинно высказывание:
1) Антон 2) Федор 3) Елена 4) Вадим
Для какого имени истинно высказывание:
1) Иван 2) Петр 3) Елена 4) Павел
4) Для какого слова ложно высказывание:
1) кенгуру 2) антилопа 3) ящерица 4) крокодил
5) Для какого слова истинно высказывание:
1) гаоцин 2) скворец 3) ласточка 4) моёвка

Задания
Заполните таблицу истинности логических
выражений:
1)
2)
3)

Задания
Символом F обозначено одно из указанных ниже логических выражений от 3-х
аргументов X,Y,Z. Дан фрагмент таблицы истинности выражения F.
Какое выражение соответствует F?
1)
2)
3)

Задания
1) Какое логическое выражение равносильно выражению:
2) Какое логическое выражение равносильно выражению:
3) Какое логическое выражение равносильно выражению:

Задания
1) Каково наименьшее натуральное число X, при котором
истинно высказывание
2) Каково наибольшее целое число X, при котором
ложно высказывание
3) Каково наибольшее целое число X, при котором
истинно высказывание
4) Каково наибольшее целое число X, при котором
ложно высказывание
5) Каково наибольшее целое число X, при котором
истинно высказывание

Задания
1) Найдите значения логических A,B,C,D, при которых указанное логическое выражение ложно. Ответ запишите в виде строки из четырех символов: значений переменных A,B,C,D (в указанном порядке). Так, например, строка 0101 соответствует тому, что A=0, B=1, C=0, D=1.
a)
b)
2) Сколько различных решений имеет уравнение
где K, L, M, N - логические переменные?

Задания
В таблицах приведены запросы к поисковому серверу:
1)
Расположите номера запросов в порядке возрастания количества
страниц, которые найдёт поисковый сервер по каждому запросу.
2)
Расположите номера запросов в порядке убывания количества
страниц, которые найдёт поисковый сервер по каждому запросу.
3)
Расположите номера запросов в порядке возрастания количества
страниц, которые найдёт поисковый сервер по каждому запросу.

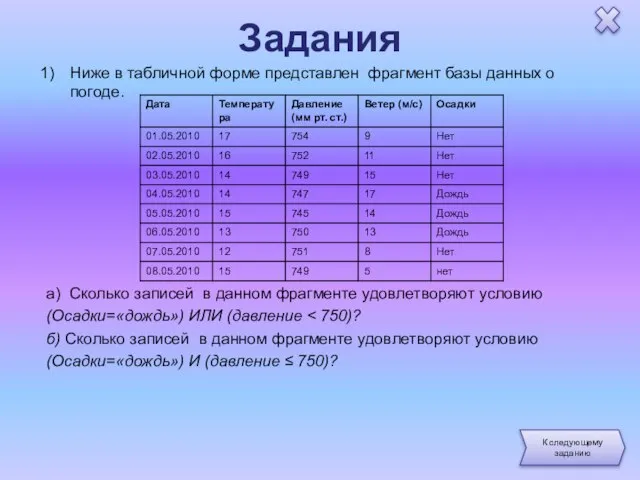
Задания
Ниже в табличной форме представлен фрагмент базы данных о погоде.
a) Сколько записей в данном фрагменте удовлетворяют условию
(Осадки=«дождь») ИЛИ (давление < 750)?
б) Сколько записей в данном фрагменте удовлетворяют условию
(Осадки=«дождь») И (давление ≤ 750)?
К следующему заданию

Задания
2) В таблице приведены данные о составе и калорийности некоторых продуктов:
Сколько записей в данной таблице удовлетворяют условию:
Вода>85 ИЛИ (белки+углеводы<11 И ккал>38) ?