Логика высказываний Математическая логика

Логические представления – описание системы, процесса или явления в виде совокупности сложных высказываний, составленных из простых (элементарных) высказываний и логических связок между ними.
Логические представления и их составляющие характеризуются определёнными свойствами и набором допустимых преобразований, реализующих правильные методы рассуждений – законы логики, разработанные в формальной (математической) логике.

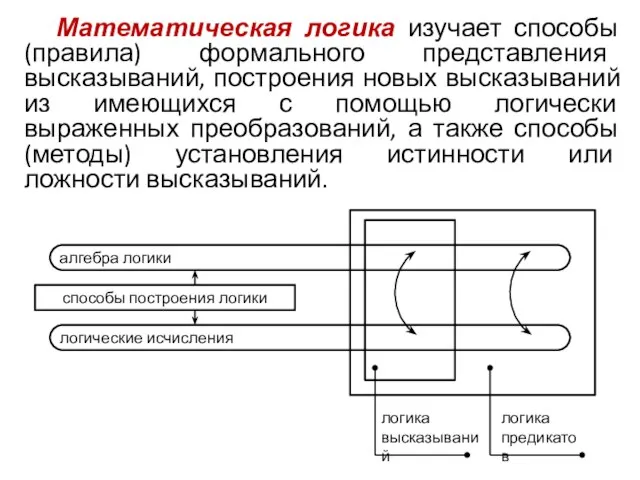
Математическая логика изучает способы (правила) формального представления высказываний, построения новых высказываний из имеющихся с помощью логически выраженных преобразований, а также способы (методы) установления истинности или ложности высказываний.
алгебра логики
логические исчисления
способы построения логики
логика
высказываний
логика
предикатов

Основными объектами разделов логики являются высказывания.
Высказывание – последовательное предложение (утверждение, суждение), о котором можно говорить, что оно истинно или ложно. Для того, чтобы оперировать высказываниями, необходимо знать их истинное значение (истинность).

2.1. Основные понятия
Простое (элементарное) высказывание рассматривается как неделимое целое. Обычно это высказывания, не содержащие логических связок.
Сложное (составное) высказывание – составляется из простых с помощью логических связок.
«и» «или» «не»
«если… то…»
«либо… либо…» (в разделительном смысле), «тогда и только тогда»
и др.

Основные логические связки (операции) логики высказываний
1. Конъюнкция (операция «и», логическое произведение)
P&Q, P∧Q, P∙Q «P и Q»
2. Дизъюнкция (операция «или», логическая сумма)
P∨Q, P+Q «P или Q»
Примечание: Понимается как неразделительное «или».

3. Отрицание (инверсия)
P, P «не P», «неверно, что P»
4. Импликация (логическое следование)
P→Q, P⊂Q
«если P, то Q», «P влечет Q», «из P следует Q»
P - посылка импликации, Q - заключение
5. Эквивалентность (равнозначность)
P∼Q, P≡Q, P↔Q
«P эквивалентно Q»,
«P, если и только если Q»

6. Неравнозначность (исключающее «или»)
P⊕Q, P∆Q
«либо P, либо Q», «или P, или Q»
Примечание: Понимается в разделительном смысле.

Алфавит логики высказываний – буквы, обозначающие высказывания, логические связки, скобки.
Логическая формула – выражение, составленное из обозначений высказываний, связок и скобок , удовлетворяющие условиям:
1. Любая переменная, обозначающая высказывание, - формула.
2. Если A и B – формулы, то (A∧B), (A∨B), A, A→B, A↔B, A⊕B – формулы.
3. Других формул нет.

Пример 1
Представить логическими формулами следующие высказывания:
Сегодня понедельник или вторник.
Идёт дождь или снег.
Если идёт дождь, то крыши мокрые. Дождя нет, а крыши мокрые.
Что в лоб, что по лбу.
A⊕B
A∨B
(A→B)&(A&B)
A∼B