Основы теории множеств

Бинарные отношения и их свойства
Отношение - частный случай соответствия, когда область прибытия совпадает с областью отправления:
R ⊆ A × A
A×A=А2 называется квадратом множества А.
R ⊆ A2

Формы задания отношений
Пример: Пусть A = { a, b, c, d }
1 форма - как множества:
R = { < a, b >,
< b, a >, < b, b >, < b, c >,
< c, d > }

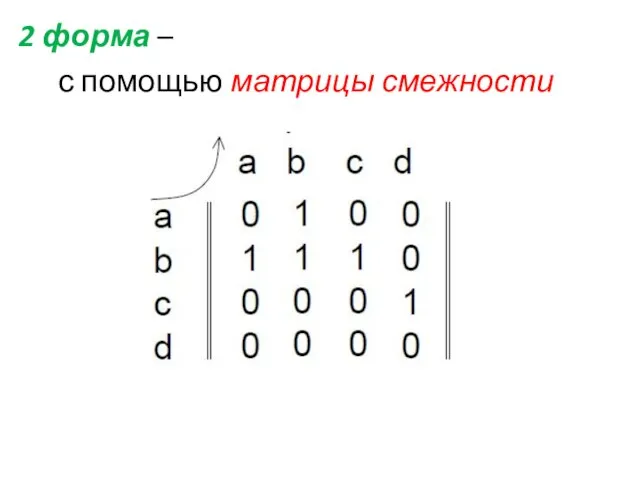
2 форма –
с помощью матрицы смежности

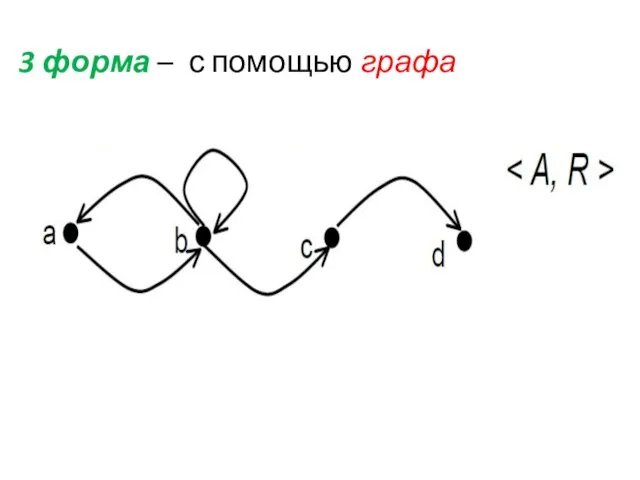
3 форма – с помощью графа

Свойства отношений
Пусть дано R ⊆ A × A.
Тот факт, что < a, b > ∈ R будем обозначать также как a R b
1. Рефлексивность
Для всех x∈ A верно, что x R x
Все элементы лежащие на главной диагонали матрицы смежности равны 1.
Определим диагональное отношение как δ = { < a, a > | a ∈ A }.

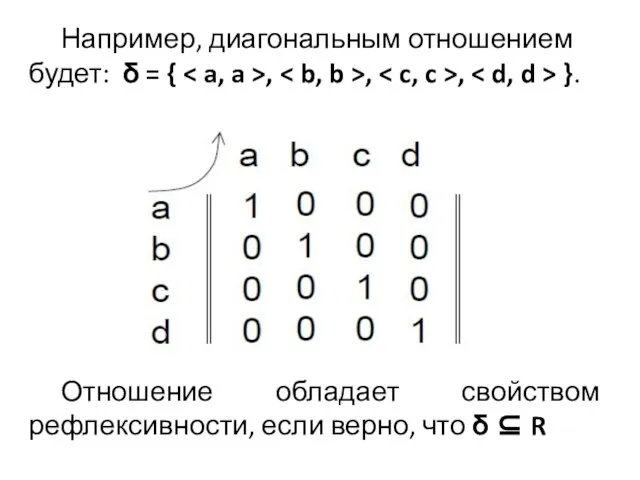
Например, диагональным отношением будет: δ = { < a, a >, < b, b >, < c, c >, < d, d > }.
Отношение обладает свойством рефлексивности, если верно, что δ ⊆ R

2. Антирефлексивность
Из x R y следует, что x ≠ y
R ∩ δ = ∅

3. Симметричность
Из x R y следует, что y R x
Матрица смежности симметричного отношения является симметричной относительно главной диагонали, а при задании отношения в виде графа следствием симметричности является наличие между всякой парой вершин, находящихся в отношении R, двух противоположно направленных дуг.
Отношение R симметрично, если и только если
R = R –1

4. Асимметричность
Из < x, y > ∈ R следует, что < y, x > ∉ R
В соответствующем графе нет петель и не может быть случая, когда две вершины соединены двумя противоположно направленными дугами.
Если отношение асимметрично, то оно
антирефлексивно.
Отношение R асимметрично, если и только если
R ∩ R –1 = ∅

5. Антисимметричность
Из < x, y > ∈ R следует, что < y, x > ∉ R
Из < x, y > ∈ R и < y, x > ∈ R следует,
что x = y
Отношение R антисимметрично, если и только если
R ∩ R–1 ⊆ δ

6. Транзитивность
x, y, z ∈ A
Из < x, y>∈ R и < y, z>∈ R следует,
что < x, z> ∈ R
Отношение R транзитивно, если и только если R ° R ⊆ R.
Равенство достигается, если транзитивное отношение ещё и рефлексивно.

Транзитивное замыкание
Пусть дано отношение R ⊆ A × A. Тогда его транзитивным замыканием будет отношение
R^ ⊆ A × A минимальное по числу элементов (пар) и такое, что оно обладает свойством транзитивности и R ⊆ R^ .
∈ R^ если существует цепочка элементов из А х = z0, z1, … zn = y такая, что
z0 R z1, z1 R z2, … zn-1 R zn
Если R транзитивно, то R = R^.

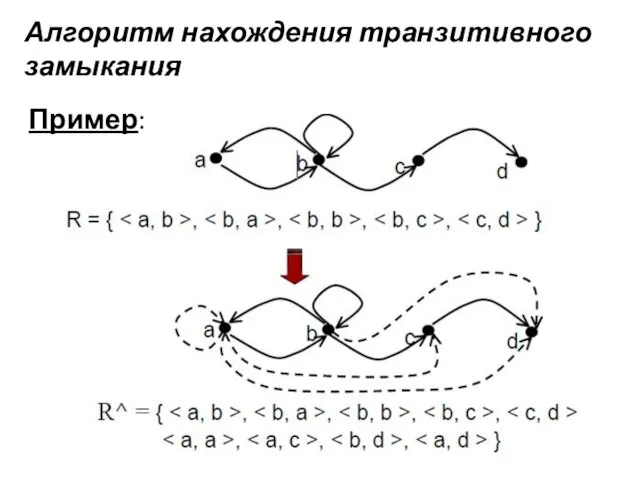
Алгоритм нахождения транзитивного замыкания
Пример:

Cодержательно транзитивное замыкание определяется всеми путями, существующими в графе (начальная и конечная вершины пути определяют соответствующую пару).
R - есть все пути длиной 1 (из 1-й дуги),
R2 = R ° R - есть все пути длиной 2 (из 2-х дуг),
R3 = R° R° R - есть все пути длиной 3 (из 3-х дуг),
… и т.д.
R^ = R1 ∪ R2 ∪ R3 ∪ … ∪ Rn ∪ …

Вычисление транзитивного замыкания заданного отношения
R* есть текущее множество (отношение)
В начале вычисления имеем
R*1 =R={< a, b >, < b, a >, < b, b >,< b, c >, < c, d>}
R2 = R ° R =
{< a, a >, < a, b >,< b, c >, < a, c >, < b, b >, < b, d >}
R*2 = {< a, b >, < b, a >, < b, c >, < c, d > < a, a >,
< a, c >, < b, b >, < b, d >}