Магические квадраты.

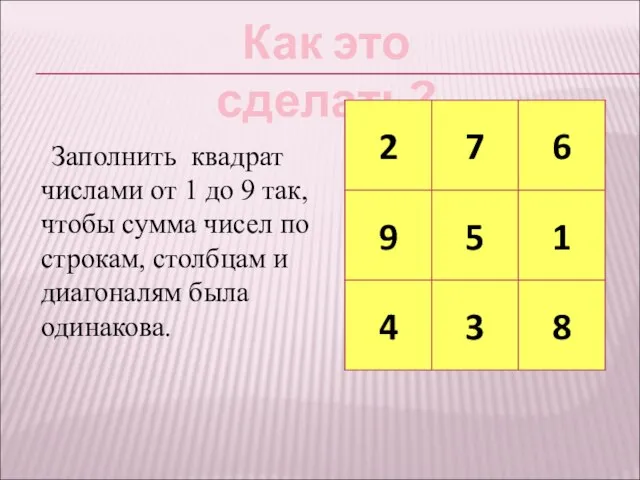
Заполнить квадрат числами от 1 до 9 так, чтобы сумма чисел по строкам, столбцам и диагоналям была одинакова.
Как это сделать?

Цель работы:
Выяснить различные способы составления магических квадратов и изучить области их применения.

познакомиться с историей появления магических квадратов;
рассмотреть виды магических квадратов и способы их заполнения;
выяснить области применения магических квадратов.
Задачи:

а
а
а
а
а
а
а
а
а

Альбрехт Дюрер. «Меланхолия»
16
3
2
13
5
10
11
8
9
6
7
12
4
1

16
3
2
5
10
11
9
6
7
Квадрат Дюрера - магический!
16+
3+
5+
10+
11+
8=
12=
9+
6+
7+
4
15
14
13
8
12
1
13=
4+
15+
14+
1= 34
34
34
34
2+
Найдем сумму цифр в каждой строке.

16
3
2
5
10
11
9
6
7
16+
5+
9+
3+
10+
6+
15=
14=
2+
11+
7+
4
15
14
13
8
12
1
4=
13+
8+
12+
1=
Квадрат Дюрера - магический!
34
34
34 34
Найдем сумму цифр в каждом столбце.

16
3
2
5
10
11
9
6
7
Квадрат Дюрера - магический!
16+
10+
7+
13+
11+
6+
4=
4
15
14
13
8
12
1
1=
Найдем сумму цифр
в каждой диагонали. 34
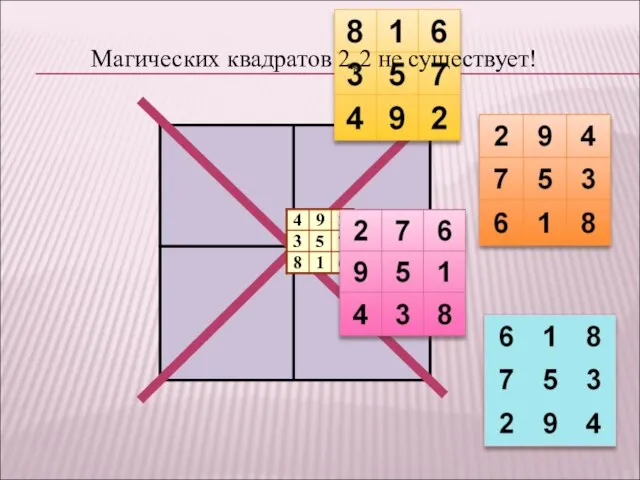
34

Магических квадратов 2*2 не существует!

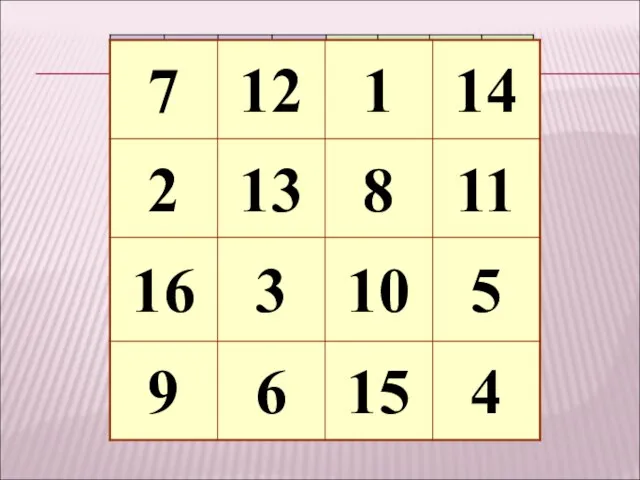
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*

Игра шаффлборд очень популярна в Англии среди аристократов.

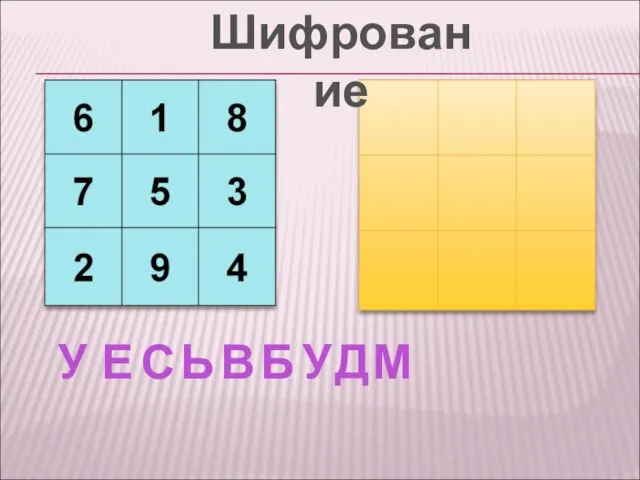
У
Е
С
Ь
В
Б
У
Д
М
Шифрование

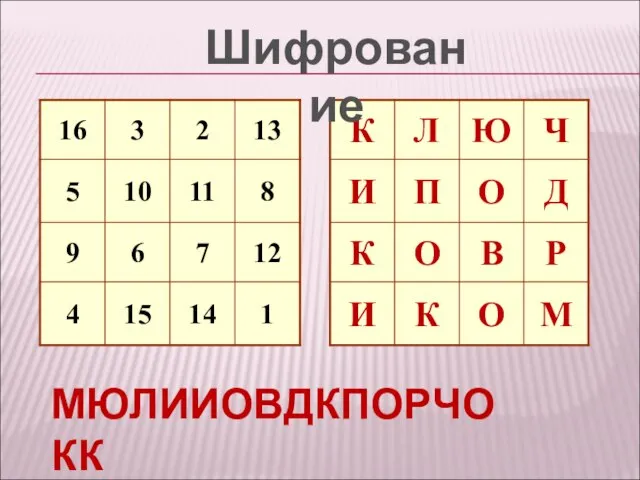
Шифрование
МЮЛИИОВДКПОРЧОКК

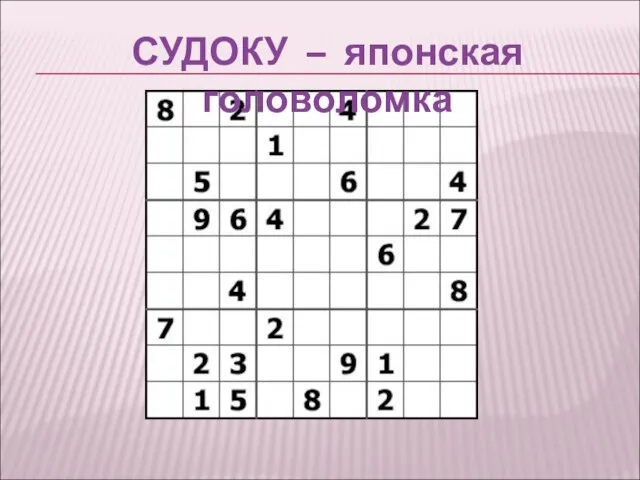
СУДОКУ – японская головоломка

КВАДРАТ ПИФАГОРА
28.07.1998
Складываем числа дня, месяца и года рождения,
2+8+0+7+1+9+9+8=44
получаем первое рабочее число 44.
Складываем цифры первого рабочего числа
4+4=8
и получаем второе рабочее число 8.
Из первого рабочего числа вычитаем удвоенную первую цифру дня рождения, так получается третье рабочее число:
44-(2*2)=40
Четвертое рабочее число получаем из суммы цифр третьего рабочего числа:
4+0=4

Мой магический квадрат
28071998 448404

ВЫВОДЫ:
Познакомилась с историей появления магических квадратов;
Рассмотрела виды магических квадратов и способы их заполнения;
Научилась заполнять магические квадраты по методу достроения, методу А. де Лубера, методу заполнения квадратов порядка 2n
Выяснила области применения магических квадратов.