Математический язык. Математическая модель

Цель: повторяя материал курса математики 5–6 классов, ввести термины: математический язык, математическая модель, не давая им строгого обоснования; дать учащимся возможность привыкнуть к этим терминам и включить их в свой рабочий словарь, то есть заложить фундамент математического языка.

Числовые и алгебраические выражения
Что такое математический язык
Что такое математическая модель
Линейное уравнение с одной переменной
Координатная прямая

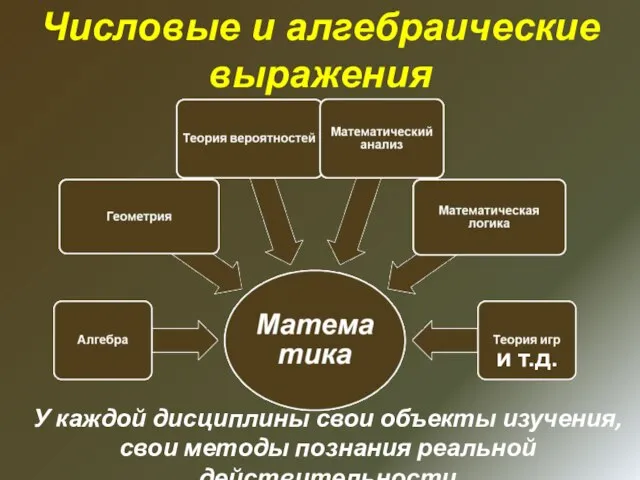
и т.д.
У каждой дисциплины свои объекты изучения, свои методы познания реальной действительности
Числовые и алгебраические выражения

Числовым выражением называют всякую запись, составленную из чисел и знаков арифметических действий
Пример 1:
Обозначим числитель данного дробного выражения буквой А, а знаменатель – буквой В и выясним порядок действий
А =
В =

В процессе решения примера вспомнили и применили следующие сведения:
Порядок арифметических действий.
Переместительный закон сложения: а+в=в+а.
Переместительный закон умножения: ав=ва.
Сочетательный закон сложения:
а+в+с=(а+в)+с= а+(в+с).
Понятия обыкновенной дроби, десятичной дроби, отрицательного числа.
Сочетательный закон умножения: авс=(ав)с=а(вс).
Арифметические операции с десятичными дробями.
Арифметические операции с обыкновенными дробями.
Основное свойство дроби: .
Правила действия с положительными и отрицательными числами.

Число, которое получается в результате упрощений числового выражения, называют значением числового выражения.
Если дано алгебраическое выражение, то можно говорить о значении алгебраического выражения только при конкретных значениях входящих в него букв.
Поскольку буквам, входящим в состав алгебраического выражения, можно придавать различные числовые значения (т.е. можно менять значения букв), эти буквы называют переменными.

На нуль делить нельзя!
В тех случаях, когда возникает такая ситуация делаем вывод, что выражение не имеет смысла.
Если при конкретных значениях букв (переменных) алгебраическое выражение имеет значение, то указанные значения переменных называют допустимыми; если же при конкретных значениях букв (переменных) алгебраическое выражение не имеет смысла, то указанные значения переменных называют недопустимыми.

Что такое математический язык
Цель: сформировать понимание учащимися того, что математика – предмет, позволяющий правильно ориентироваться в окружающей действительности; предмет, который реальные процессы описывает на особом математическом языке. Познакомить учащихся с некоторыми символами, правилами математического языка.

На математическом языке многие утверждения выглядят яснее и прозрачнее, чем на обычном. Во всяком языке есть письменная и устная речь.
В математике устная речь – это употребление специальных терминов («слагаемое», «уравнение», «неравенство», «график», «координата» и т.п.), а так же различные математические утверждения, выраженные словами.

Вывод
главное назначение математического языка – способствовать организации деятельности.

Что такое математическая модель
Цель: сформировать понимание учащимися сути термина «математическое моделирование». Привести примеры, показывающие, как может математика описывать реальные процессы на особом математическом языке в виде математических моделей. Познакомить учащихся с тремя этапами математического моделирования и выработать умение применять полученные знания на практике.

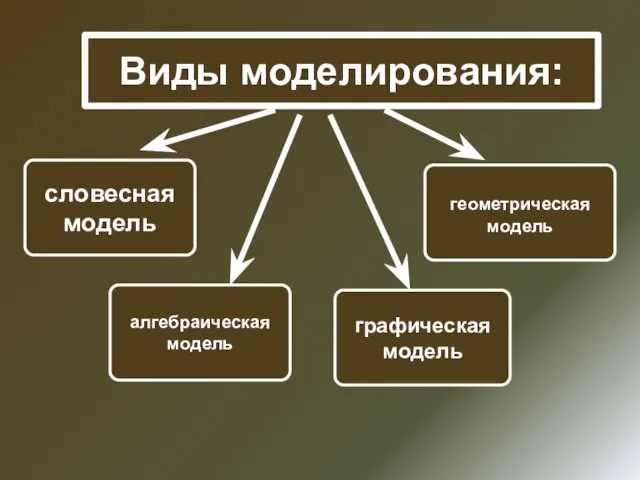
Виды моделирования:
словесная модель
геометрическая модель
алгебраическая модель
графическая модель

Алгебра занимается тем, что описывает различные реальные ситуации на математическом языке в виде математических моделей, а затем имеет дело уже не с реальными ситуациями, а с этими моделями, используя разные правила, свойства, законы, выработанные в алгебре.
При решении математических задач рассуждения проходят три этапа:
Составление математической модели;
Работа с математической моделью;
Ответ на вопрос задачи.

Линейное уравнение с одной переменной
Цель: повторить известные из курса 5–6 класса линейные уравнения с одной переменной, отработать алгоритм решения линейного уравнения.

Одним из самых простых и в то же время очень важных видов математических моделей реальных ситуаций являются известные вам из курса математики 5-6 классов линейные уравнения с одной переменной (приведите примеры).

Что значит решить линейное уравнение ?
Решить линейное уравнение – это значит найти все те значения переменной, при каждом из которых уравнение обращается в верное числовое равенство или ... ?

Линейным уравнением с одной переменной x называют уравнение вида ax+b=0, где a и b – любые числа (коэффициенты)
Если а=0 и b=0, т.е. уравнение имеет вид 0⋅x+0=0, то корнем уравнения является любое число (бесконечное множество корней).
Если а=0 и b≠0, т.е. уравнение имеет вид 0⋅x+b=0, то уравнение не имеет корней.

Алгоритм
решения линейного уравнения ax+b=0 в случае, когда a≠0
Преобразовать уравнение к виду a x = - b.
Записать корень уравнения в виде x = (- b): a, или, что то же самое, .

Алгоритм
решения линейного уравнения
Если уравнение содержит скобки, то их надо открыть по правилу раскрытия скобок (Если перед скобками стоит знак «-», то …; если перед скобками стоит знак «+», то …).
Перенести все члены уравнения, содержащие переменную в одну часть, а не содержащие переменную в другую (При переносе из одной части уравнения в другую, знаки слагаемых меняются на противоположные).
Привести подобные слагаемые и получить уравнение вида a x = - b.
Применить алгоритм решения простейших линейных уравнений с одной переменной.

Методы и приемы
применяемые при решении уравнений
Приведение подобных слагаемых
Правила раскрытия скобок
Прием переноса слагаемых
Свойство пропорций (перекрестное правило)
Приведение к целым коэффициентам

Цель: повторить понятие координатной прямой (координатной оси), правило нахождения точки по заданной координате и правило отыскания координаты заданной точки. Познакомить учащихся с видами числовых промежутков. Обучить умению непринужденно связывать геометрическую и аналитическую модели промежутка и выбирать адекватное обозначение и символическую запись.
Координатная прямая

Нужно уметь свободно переходить от одного вида математической модели к другому, выбирать то, что удобнее. В этой связи весьма полезна графическая модель – координатная прямая.
О
0
х
1
Прямая, начало отсчета, масштаб, положительное направление

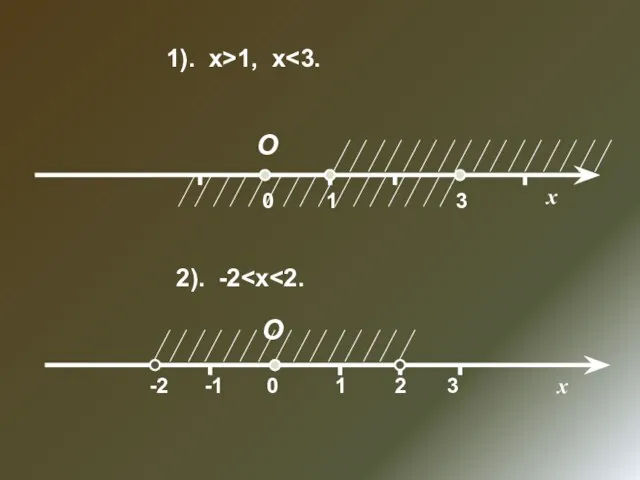
О
0
х
1 3
1). х>1, х<3.
2). -2<х<2.
О
0
х
-2 -1 1 2 3

Сводная таблица числовых промежутков

Привести примеры:
числовых выражений;
алгебраических выражений;
порядка выполнения действий в числовых выражениях;
переместительного и сочетательного законов сложения и умножения;
понятия обыкновенной дроби, десятичной дроби, отрицательного числа;
арифметических операций с обыкновенными и десятичными дробями;
основного свойства обыкновенной дроби;
правил действий с положительными и отрицательными числами.

№1. Укажите числовые и буквенные выражения
А) 4,16+2,5+6,04+3,5; Б) х+5;
В) 8с - 12d; Г) ;
Д) ; Е) -9⋅1,5 +8,3(-7,8-(-3,3)).
Подумай! №34; 35; 36
№ 2. Выполни действия удобным способом:
а) б)