Содержание
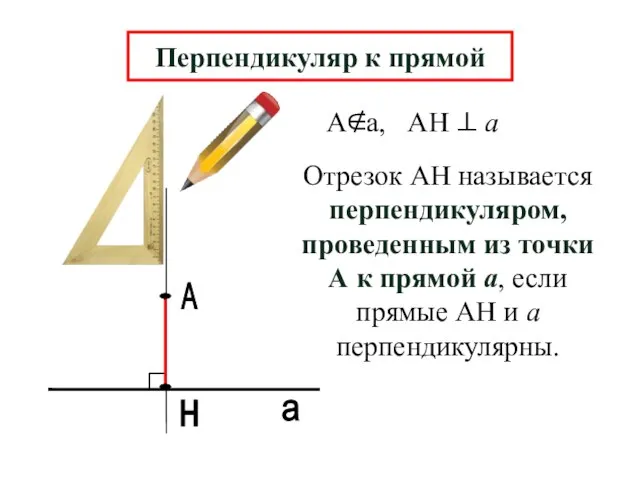
- 2. А н а Перпендикуляр к прямой Отрезок АН называется перпендикуляром, проведенным из точки А к прямой
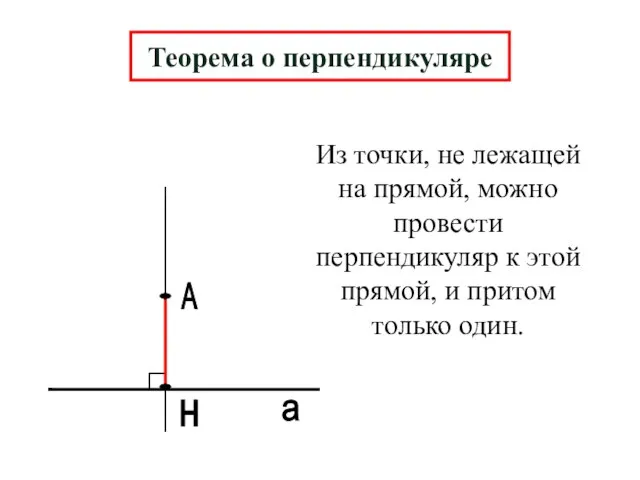
- 3. А н а Теорема о перпендикуляре Из точки, не лежащей на прямой, можно провести перпендикуляр к
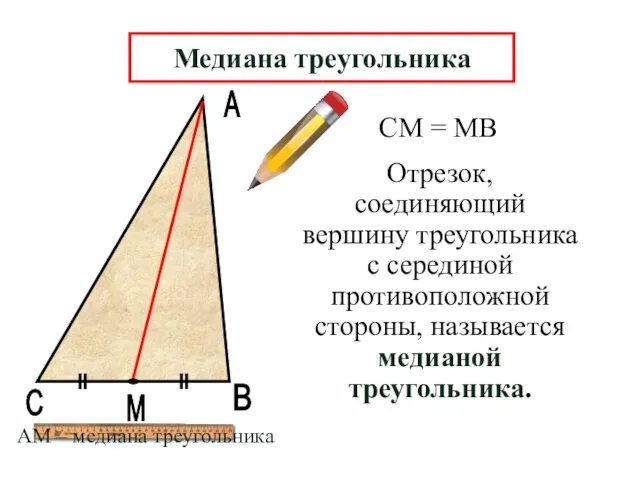
- 4. А В М Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется медианой треугольника. С СМ
- 5. Медиана-обезьяна, У которой зоркий глаз, Прыгнет точно в середину Стороны против вершины, Где находится сейчас? Медиана
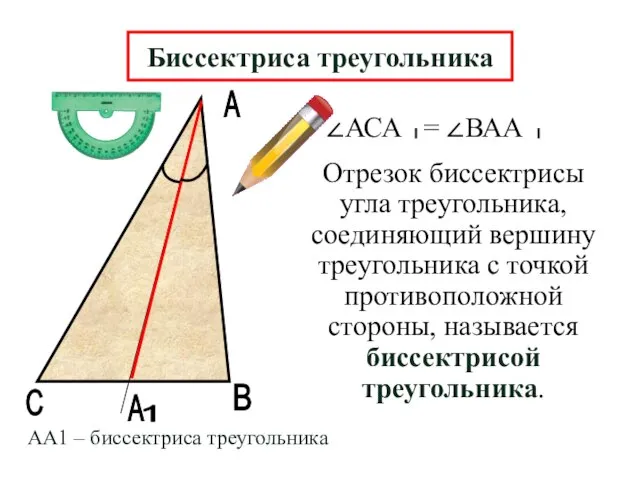
- 6. А В А Отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны, называется биссектрисой
- 7. Биссектриса треугольника Биссектриса – это крыса, Которая бегает по углам И делит угол пополам.
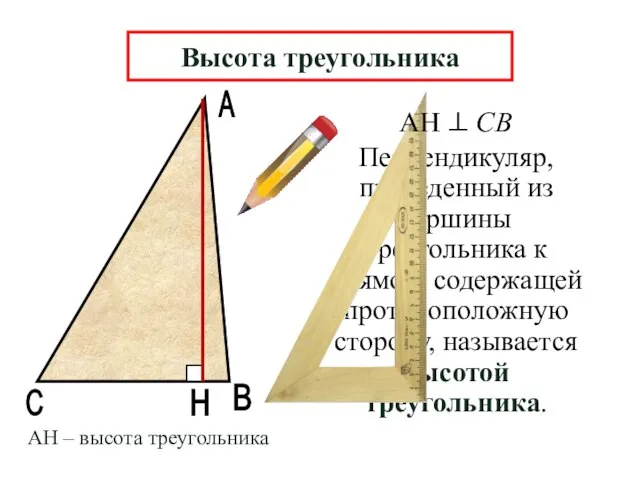
- 8. А В Н Перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону, называется высотой треугольника.
- 9. Высота треугольника Высота похожа на кота, Который, выгнув спину, И под прямым углом Соединит вершину И
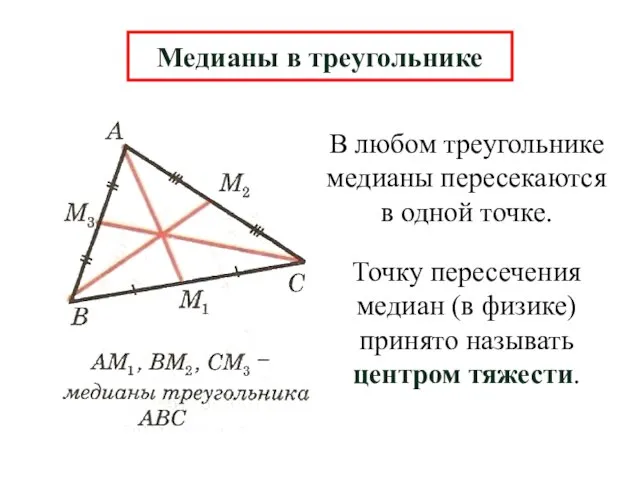
- 10. В любом треугольнике медианы пересекаются в одной точке. Медианы в треугольнике Точку пересечения медиан (в физике)
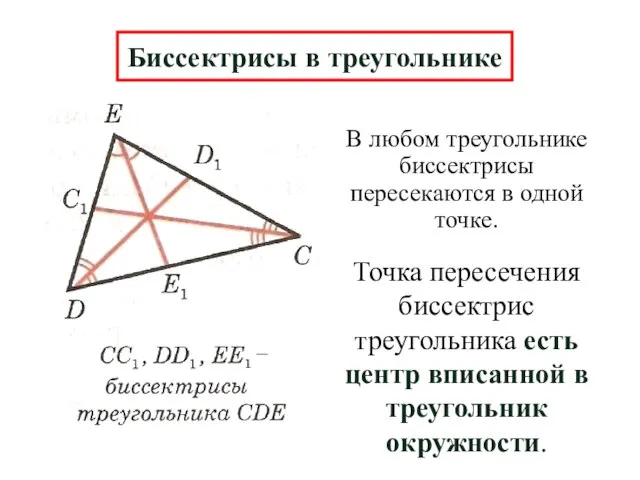
- 11. В любом треугольнике биссектрисы пересекаются в одной точке. Биссектрисы в треугольнике Точка пересечения биссектрис треугольника есть
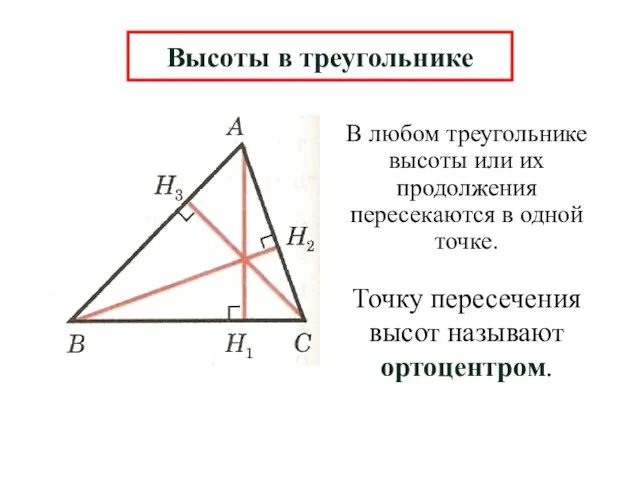
- 12. Высоты в треугольнике
- 13. В любом треугольнике высоты или их продолжения пересекаются в одной точке. Высоты в треугольнике Точку пересечения
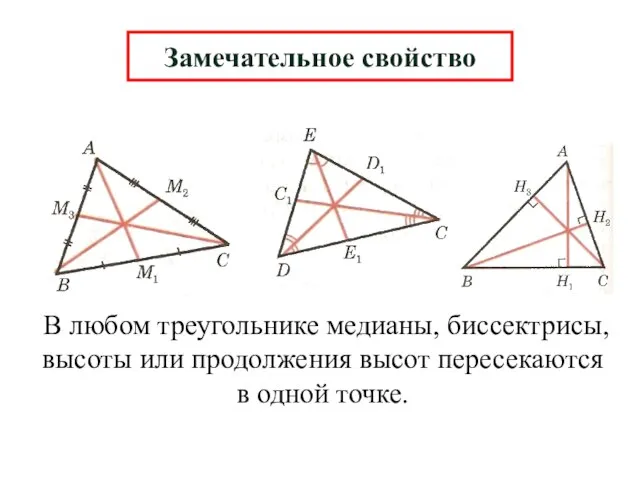
- 14. Замечательное свойство В любом треугольнике медианы, биссектрисы, высоты или продолжения высот пересекаются в одной точке.
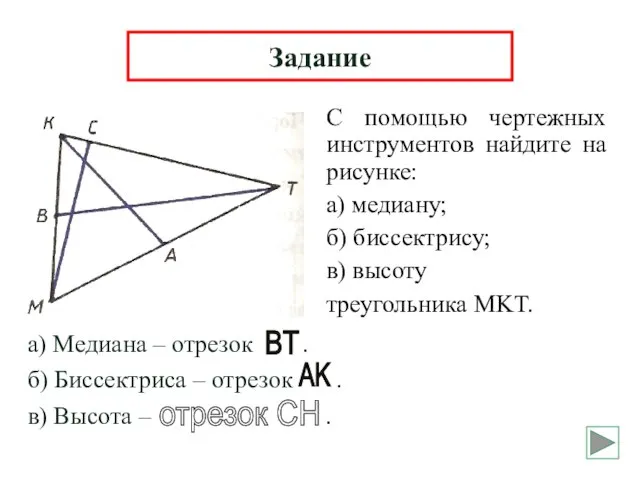
- 15. С помощью чертежных инструментов найдите на рисунке: а) медиану; б) биссектрису; в) высоту треугольника MKT. Задание
- 16. I уровень: п. 16,17, знать основные определения и формулировки утверждений и теорем. II уровень: п. 16,17,
- 18. Скачать презентацию





 Изображения изделий и их обозначения при выполнении графических конструкторских документов
Изображения изделий и их обозначения при выполнении графических конструкторских документов Использование функций
Использование функций Математические задачи от русских, советских и зарубежных писателей
Математические задачи от русских, советских и зарубежных писателей Каникулы в международном детском лагере
Каникулы в международном детском лагере Язык есть исповедь народа
Язык есть исповедь народа Работа по стимулированию юридических лиц и индивидуальных предпринимателей к трудоустройству безработных
Работа по стимулированию юридических лиц и индивидуальных предпринимателей к трудоустройству безработных Физико-географическое районирование Северной Евразии
Физико-географическое районирование Северной Евразии  Узоры “тетёрки ” на печенье
Узоры “тетёрки ” на печенье Презентация на тему Постоянные магниты
Презентация на тему Постоянные магниты Весенний фестиваль для учащихся
Весенний фестиваль для учащихся 23 февраля. Поздравляем!
23 февраля. Поздравляем! Российский государственный университет нефти и газа имени И.М.Губкина Кафедра машин и оборудования нефтяной и газовой промышленн
Российский государственный университет нефти и газа имени И.М.Губкина Кафедра машин и оборудования нефтяной и газовой промышленн Звук и свет в лирике И. Анненского
Звук и свет в лирике И. Анненского Книжка-раскраска
Книжка-раскраска Взаимодействие научного руководителя со студентами через личный кабинет с использование сервиса Антиплагиат
Взаимодействие научного руководителя со студентами через личный кабинет с использование сервиса Антиплагиат Зачем живые организмы запасают питательные вещества?
Зачем живые организмы запасают питательные вещества? Особенности приема 2020 (колледж). Дистанционная подача документов
Особенности приема 2020 (колледж). Дистанционная подача документов Ресурсный Центр «Кристина»
Ресурсный Центр «Кристина» Проверка правильности кирпичной кладки
Проверка правильности кирпичной кладки Смешанное обучение – blended learning
Смешанное обучение – blended learning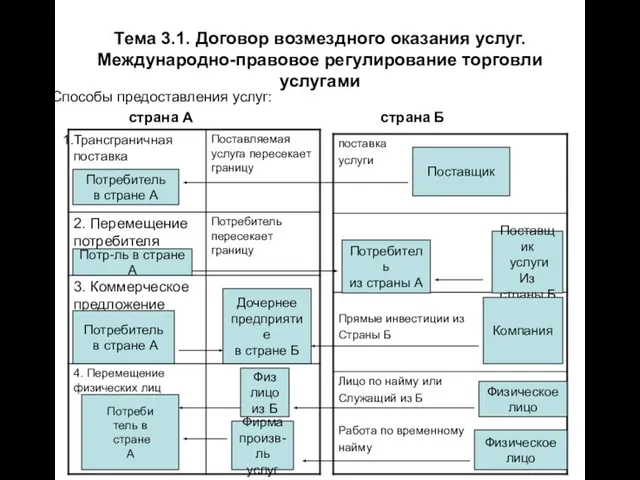 Тема 3.1. Договор возмездного оказания услуг. Международно-правовое регулирование торговли услугами Способы предоставления услуг
Тема 3.1. Договор возмездного оказания услуг. Международно-правовое регулирование торговли услугами Способы предоставления услуг Конвенция о правах ребенка
Конвенция о правах ребенка Богомолова Роза Александровна
Богомолова Роза Александровна Renault Assistance. Служба маркетинга запасных частей и послепродажного обслуживания
Renault Assistance. Служба маркетинга запасных частей и послепродажного обслуживания Принцип действия жидкокристаллических дисплеев
Принцип действия жидкокристаллических дисплеев Правила работы с обучающей презентацией
Правила работы с обучающей презентацией плакат
плакат ОП по Гагинскому району МО МВД России Большеболдинский: история, сегодняшнее состояние и перспективы развития
ОП по Гагинскому району МО МВД России Большеболдинский: история, сегодняшнее состояние и перспективы развития