Содержание
- 2. Вопрос №1. Центральное и параллельное проецирование
- 3. Изготовление деталей и сборка изделий производится по чертежам. Чертежом называют документ, содержащий изображение предмета и другие
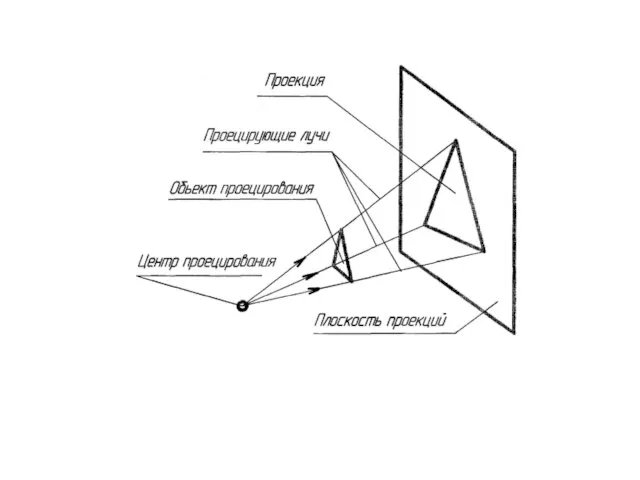
- 4. Проецирование - процесс получения изображения предмета на какой либо плоскости. Полученное изображение - проекция предмета. Элементами,
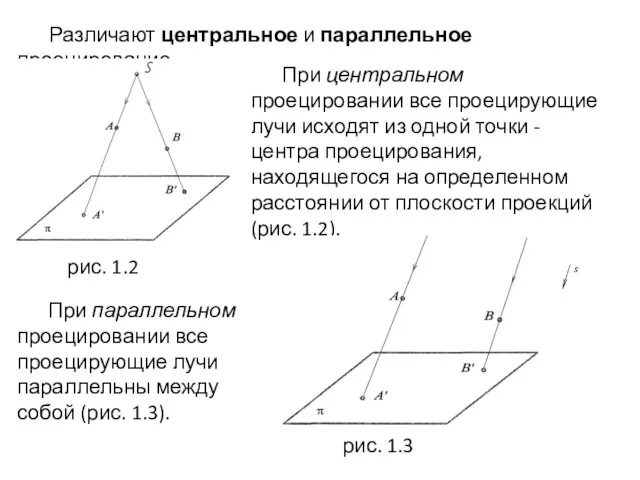
- 6. Различают центральное и параллельное проецирование. При центральном проецировании все проецирующие лучи исходят из одной точки -
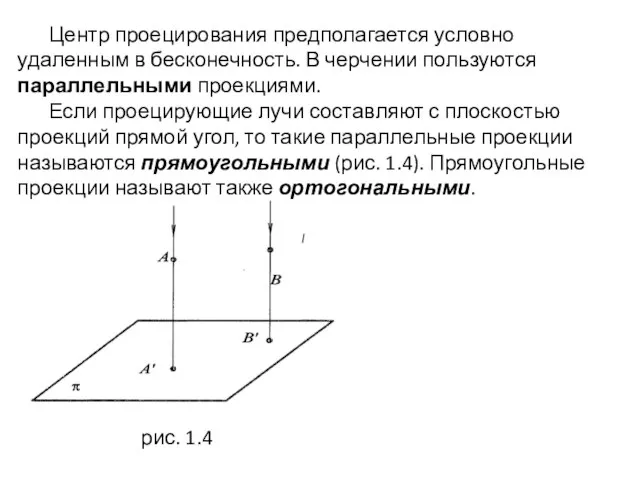
- 7. Центр проецирования предполагается условно удаленным в бесконечность. В черчении пользуются параллельными проекциями. Если проецирующие лучи составляют
- 8. Вопрос №2. Проецирование на три плоскости проекций (комплексный чертеж МОНЖА)
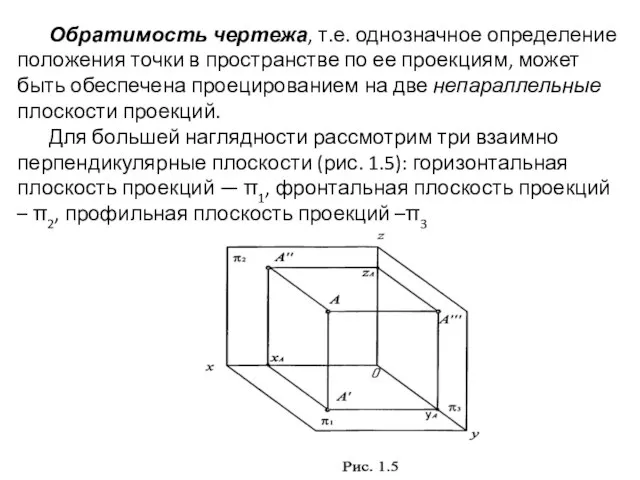
- 9. Обратимость чертежа, т.е. однозначное определение положения точки в пространстве по ее проекциям, может быть обеспечена проецированием
- 10. Линии пересечения плоскостей образуют оси координат: х – абсцисс, у — ординат, z — аппликат. Точка
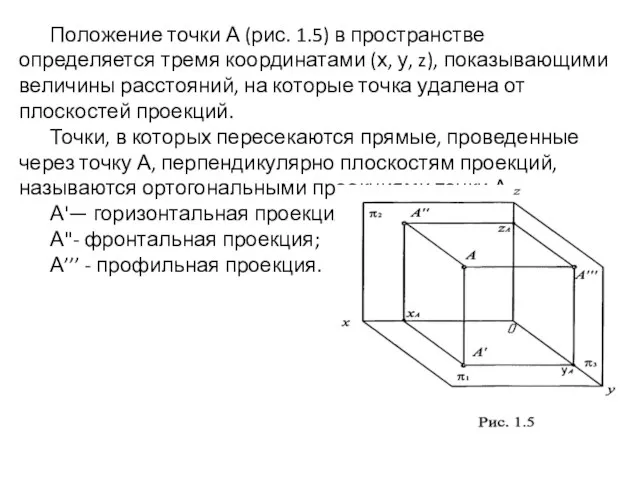
- 11. Положение точки А (рис. 1.5) в пространстве определяется тремя координатами (х, у, z), показывающими величины расстояний,
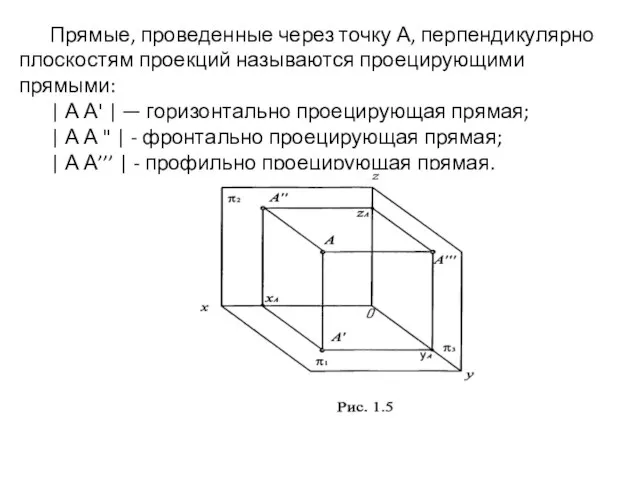
- 12. Прямые, проведенные через точку А, перпендикулярно плоскостям проекций называются проецирующими прямыми: | А А' | —
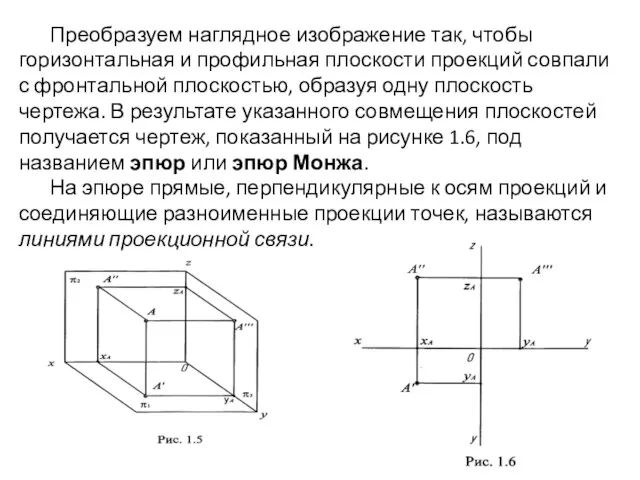
- 13. Преобразуем наглядное изображение так, чтобы горизонтальная и профильная плоскости проекций совпали с фронтальной плоскостью, образуя одну
- 14. Вопрос №3. Точки общего и частного положения
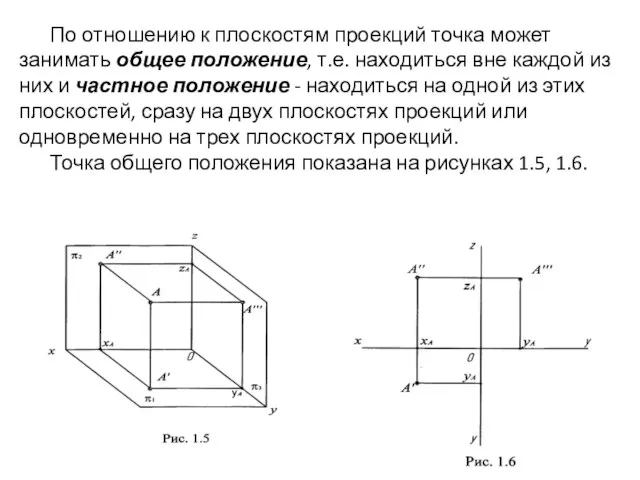
- 15. По отношению к плоскостям проекций точка может занимать общее положение, т.е. находиться вне каждой из них
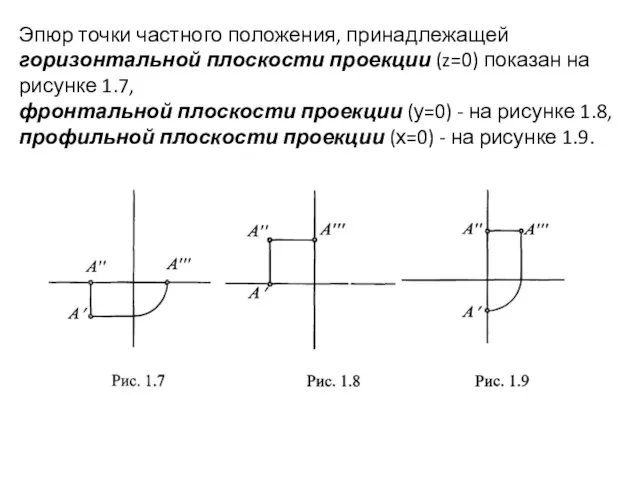
- 16. Эпюр точки частного положения, принадлежащей горизонтальной плоскости проекции (z=0) показан на рисунке 1.7, фронтальной плоскости проекции
- 17. Если точка принадлежит одновременно двум плоскостям проекций, то две ее координаты равны нулю: рисунок 1.10 -
- 18. Если точка принадлежит одновременно трем плоскостям проекций, то на эпюре все три проекции совпадают (А '=А
- 19. Вопрос №4. Проекции прямых линий
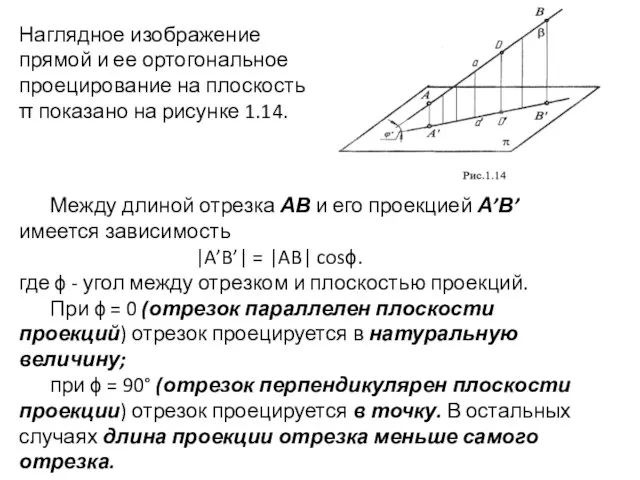
- 20. Наглядное изображение прямой и ее ортогональное проецирование на плоскость π показано на рисунке 1.14. Между длиной
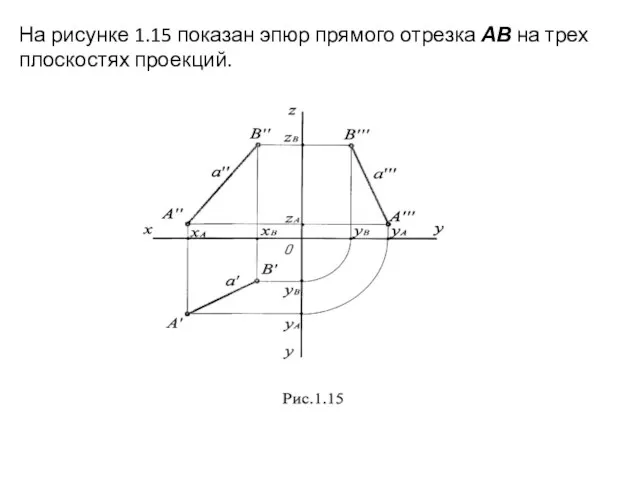
- 21. На рисунке 1.15 показан эпюр прямого отрезка АВ на трех плоскостях проекций.
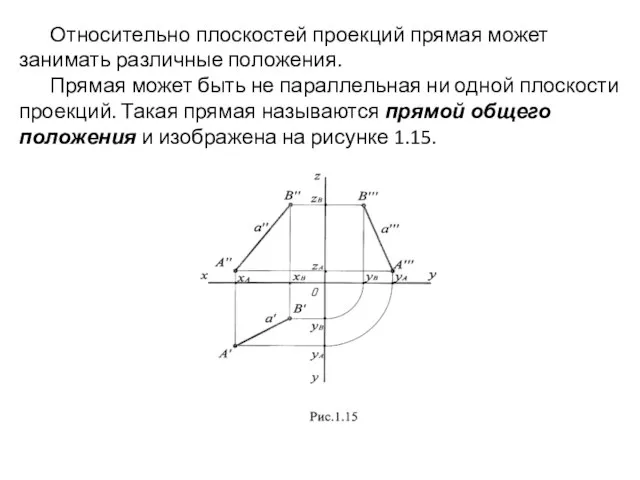
- 22. Относительно плоскостей проекций прямая может занимать различные положения. Прямая может быть не параллельная ни одной плоскости
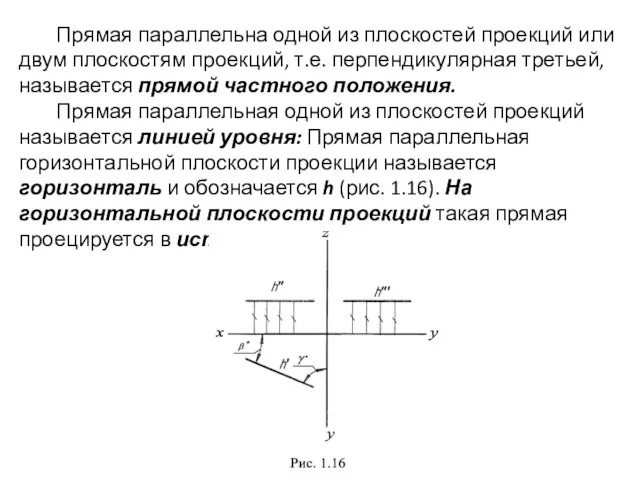
- 23. Прямая параллельна одной из плоскостей проекций или двум плоскостям проекций, т.е. перпендикулярная третьей, называется прямой частного
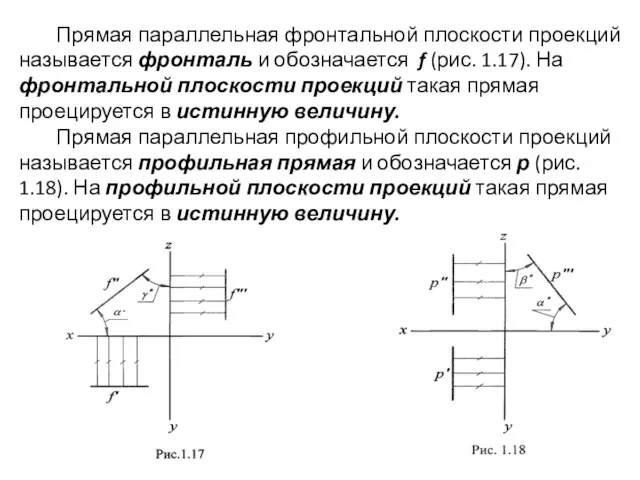
- 24. Прямая параллельная фронтальной плоскости проекций называется фронталь и обозначается f (рис. 1.17). На фронтальной плоскости проекций
- 25. Прямая, параллельная двум плоскостям проекций, перпендикулярна третьей. Такая прямая называется проецирующей. Она проецируется в точку на
- 27. Скачать презентацию










 El uso del verbo SER
El uso del verbo SER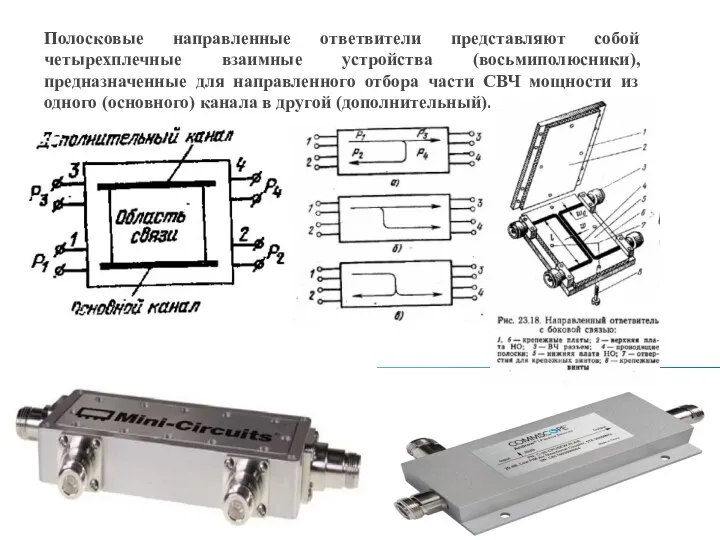 Направленные ответвители
Направленные ответвители Презентация на тему Презентация амурский тигр
Презентация на тему Презентация амурский тигр  Структура документа. Требования к оформлению документов. Лекция 4
Структура документа. Требования к оформлению документов. Лекция 4 Лексика и фразеология
Лексика и фразеология An Introduction to Software Architecture Case Studies
An Introduction to Software Architecture Case Studies Информационная система
Информационная система Западноевропейская архитектура, скульптура и живопись в X-XIV векахпрезентация Кудиновой Н.В. МОУСОШ№15 Тверь
Западноевропейская архитектура, скульптура и живопись в X-XIV векахпрезентация Кудиновой Н.В. МОУСОШ№15 Тверь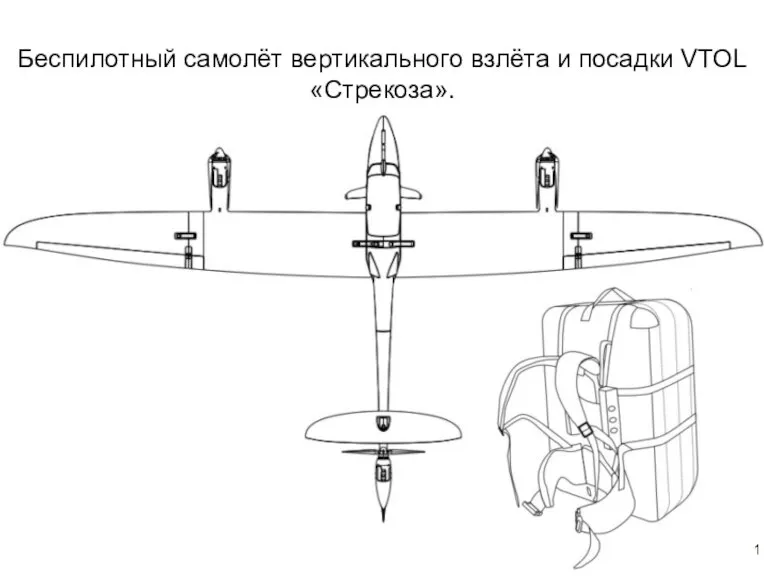 Дрон VTOL (1)
Дрон VTOL (1) Путешествие в Древний Восток
Путешествие в Древний Восток Презентация на тему Биотические факторы
Презентация на тему Биотические факторы  Банковская система и кредит. Ценные бумаги
Банковская система и кредит. Ценные бумаги СИСТЕМА ОЦЕНКИ ЗНАНИЙИ ПРИЁМЫ РАБОТЫПРИ БЕЗОТМЕТОЧНОМ ОБУЧЕНИИ В НАЧАЛЬНЫХ КЛАССАХ
СИСТЕМА ОЦЕНКИ ЗНАНИЙИ ПРИЁМЫ РАБОТЫПРИ БЕЗОТМЕТОЧНОМ ОБУЧЕНИИ В НАЧАЛЬНЫХ КЛАССАХ Школа грамотного потребителя
Школа грамотного потребителя Идентификация пользователей WiFi
Идентификация пользователей WiFi Walking Machine Technology
Walking Machine Technology Группа Компаний РОССЗОЛОТО
Группа Компаний РОССЗОЛОТО ПАО Новатэк
ПАО Новатэк Что_будет_с_рынком_недвижимости_часть_2
Что_будет_с_рынком_недвижимости_часть_2 Против коррупции
Против коррупции История создания сети интернет
История создания сети интернет С днем рождения доченька!
С днем рождения доченька! Режимы резания
Режимы резания Группа 2 Саморегулирование сети ОУ в условиях внедрения новых экономических механизмов в рамках КПМО.
Группа 2 Саморегулирование сети ОУ в условиях внедрения новых экономических механизмов в рамках КПМО. Насосы и электрооборудование насосов
Насосы и электрооборудование насосов Проект взаимодействия с нефтяными компаниями в области эффективной долгосрочной утилизации ПНГ
Проект взаимодействия с нефтяными компаниями в области эффективной долгосрочной утилизации ПНГ Тема Семинара
Тема Семинара 29 титульные листы отзывов
29 титульные листы отзывов