Содержание
- 2. Metodologie testování vlastností dřeva a materiálů na jeho bázi Statistické plánování a vyhodnocení pokusu – základní
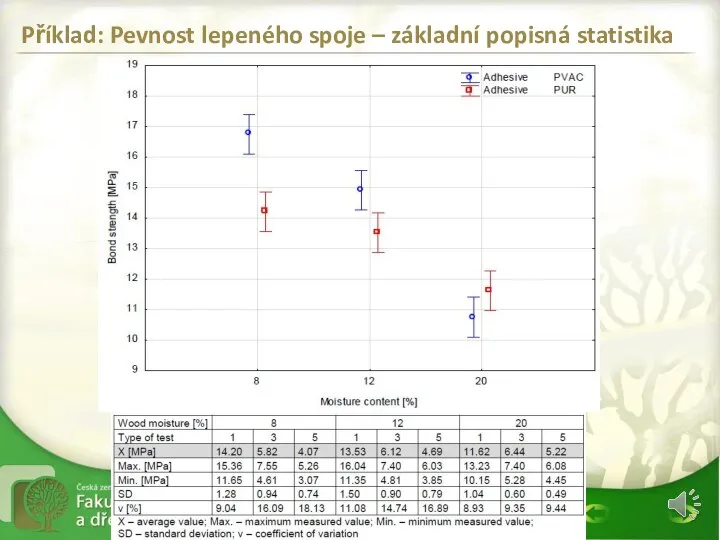
- 3. Příklad: Pevnost lepeného spoje – základní popisná statistika PVAC adhesivum na dřevo PUR adhesivum na dřevo
- 4. Příklad: Pevnost lepeného spoje – základní popisná statistika
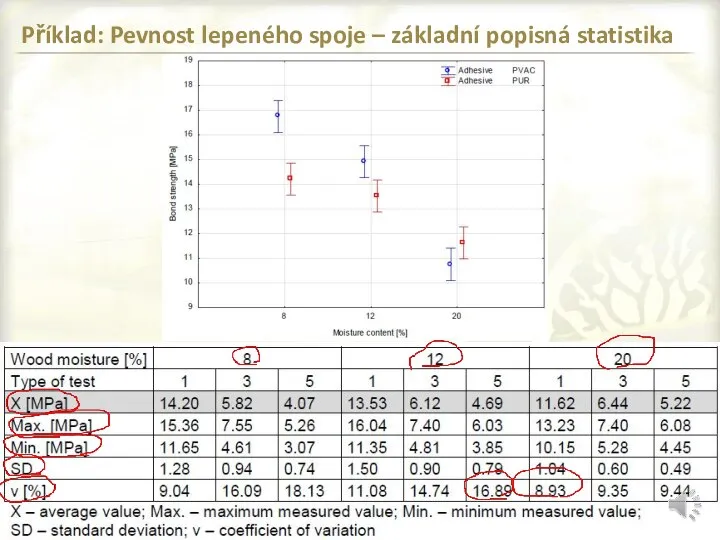
- 5. Příklad: Pevnost lepeného spoje – základní popisná statistika
- 6. Příklad: Pevnost lepeného spoje – základní popisná statistika
- 7. Statistické vyhodnocení pokusu – základní popisná statistika Aritmetický průměr: Je to součet všech hodnot (xi) vydělený
- 8. Aritmetický průměr: x = (x1 + x2 + … xn) = ∑ xi 1 1 n
- 9. Rozptyl: Rozptyl udává, jak moc jsou hodnoty v hodnoceném statistickém souboru rozptýleny. Charakterizuje rozložení hodnot ve
- 10. Výpočet rozptylu: V levé skupině máme V pravé skupině máme tři čísla: 7; 8; 9 tři
- 11. Rozptyl: Příklad: Základní popisná statistika – rozptyl σ = ∑ xi – x´2 n σ =
- 12. Směrodatná odchylka: Směrodatná odchylka, podobně jako rozptyl, určuje jak moc jsou hodnoty rozptýleny či odchýleny od
- 13. Směrodatná odchylka: Příklad: Základní popisná statistika – směrodatná odchylka s = √ σ V levé skupině
- 14. Variační koeficient: Variační koeficient je charakteristikou variability rozdělení pravděpodobností náhodní veličiny. Je to podíl směrodatné odchylky
- 15. Variační koeficient: Uvádí sourodost / reprezentativnost statistického výběru Variační koeficient, který je větší než 50%, ukazuje
- 16. Variační koeficient: Uvádí se v procentech Příklad: Základní popisná statistika – variační koeficient vk = .
- 17. Statistické vyhodnocení pokusu – medián Medián: Je to je hodnota, která se nachází přesně uprostřed všech
- 18. Medián: Příklad: Základní popisná statistika – medián V levé skupině máme V pravé skupině máme tři
- 19. Statistické vyhodnocení pokusu – modus Modus: Je to takové hodnota statistického souboru, která má největší četnost,
- 20. Statistické vyhodnocení pokusu – kvartil Kvartil: Ve statistice kvartil jsou to tři body, které rozdělují seřazená
- 21. Kvantil: Příklad: Základní popisná statistika – medián V levé skupině máme V pravé skupině máme tři
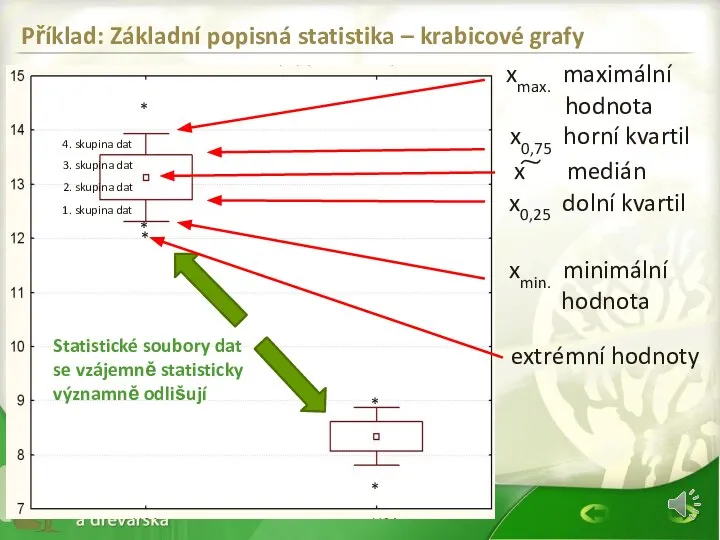
- 22. Statistické soubory dat se vzájemně statisticky významně odlišují Příklad: Základní popisná statistika – krabicové grafy x
- 23. Příklad: Stanovení počtu měřených vzorků pro testování lepeného spoje
- 24. Pomocí výběrového šetření chceme odhadnout průměrnou hodnotu pevnosti lepeného spoje dřeva. Odhad se požaduje provádět s
- 25. Stanovení počtu měřených vzorků Vychází se ze vzorce přípustné chyby odhadu průměru v základním souboru: Δ
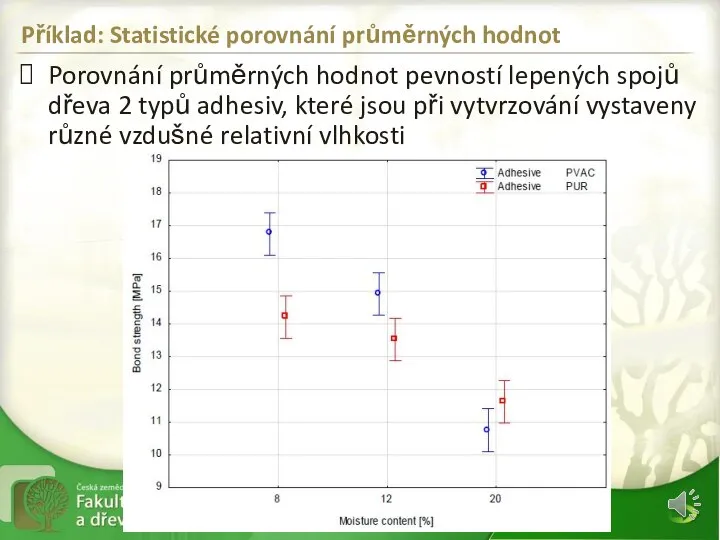
- 27. Příklad: Statistické porovnání průměrných hodnot Porovnání průměrných hodnot pevností lepených spojů dřeva 2 typů adhesiv, které
- 29. Скачать презентацию





















 Предложения с прямой речью (5 класс)
Предложения с прямой речью (5 класс) Глаз и зрение 8 класс
Глаз и зрение 8 класс Балллада как жанр. Баллада О Королева Элеонор
Балллада как жанр. Баллада О Королева Элеонор Бальцева Т.В., заведующий МДОУ центром развития ребенка- детским салом № 71
Бальцева Т.В., заведующий МДОУ центром развития ребенка- детским салом № 71 Организация работы по воспитанию навыков безопасного поведения у детей дошкольного возраста
Организация работы по воспитанию навыков безопасного поведения у детей дошкольного возраста Занятие по лепке из пластилина в программе Картонный домик
Занятие по лепке из пластилина в программе Картонный домик Основные этапы законотворческого процесса разработки Федерального Закона о закупках отдельными видами юридических лиц N223-ФЗ
Основные этапы законотворческого процесса разработки Федерального Закона о закупках отдельными видами юридических лиц N223-ФЗ Лирическая зарисовка как жанр художественной литературы
Лирическая зарисовка как жанр художественной литературы Эпоха Возрождения 7 класс
Эпоха Возрождения 7 класс Прямые линии и организация пространства
Прямые линии и организация пространства Урок математики
Урок математики Проектирование полуботинок с настрочными берцами
Проектирование полуботинок с настрочными берцами BlackRock
BlackRock Взаимодействие совокупного спроса и совокупного предложения
Взаимодействие совокупного спроса и совокупного предложения Работа и достижения Муниципального казенного учреждения культуры «Дом культуры»село ГофицкоеПетровского района Ставропольс
Работа и достижения Муниципального казенного учреждения культуры «Дом культуры»село ГофицкоеПетровского района Ставропольс Мифы
Мифы Проектирование и расчет координатной защиты башенных кранов
Проектирование и расчет координатной защиты башенных кранов Классицизм в архитектуре
Классицизм в архитектуре Введение в параллельные вычисления. Технология программирования MPI (день четвертый)
Введение в параллельные вычисления. Технология программирования MPI (день четвертый) Presentation Title
Presentation Title  Виды и формы СЭМПЛИНГА.
Виды и формы СЭМПЛИНГА. Структура фешн рынка
Структура фешн рынка Домашние животные
Домашние животные НЕОТЛОЖНЫЕ СОСТОЯНИЯ У ДЕТЕЙ.СЕРДЕЧНО-ЛЁГОЧЬНАЯ РЕАНИМАЦИЯ
НЕОТЛОЖНЫЕ СОСТОЯНИЯ У ДЕТЕЙ.СЕРДЕЧНО-ЛЁГОЧЬНАЯ РЕАНИМАЦИЯ День птиц
День птиц Влияние запахов на психоэмоциональное состояние школьников
Влияние запахов на психоэмоциональное состояние школьников Презентация на тему Местные органы власти и управления Украины в послевоенные годы (1945 - первая пол. 1960 гг.)
Презентация на тему Местные органы власти и управления Украины в послевоенные годы (1945 - первая пол. 1960 гг.) Современный международный опыт
Современный международный опыт