Содержание
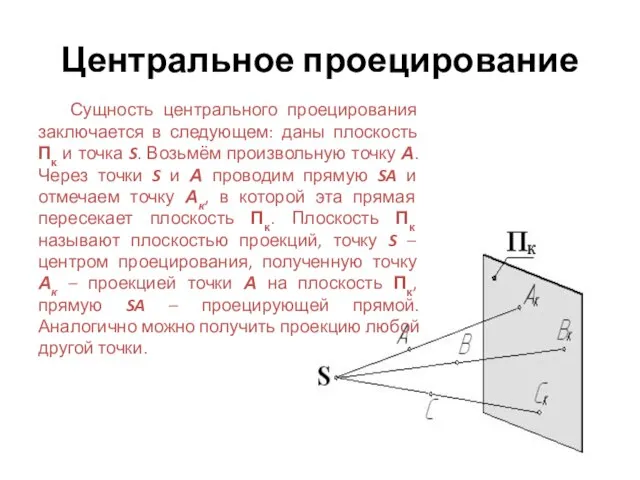
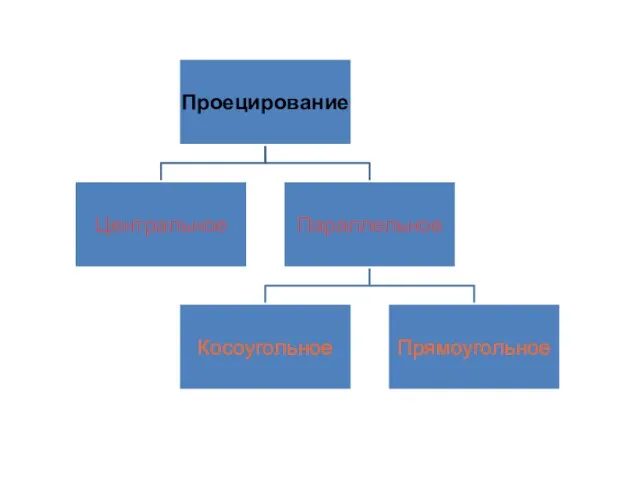
- 2. Центральное проецирование Сущность центрального проецирования заключается в следующем: даны плоскость Πк и точка S. Возьмём произвольную
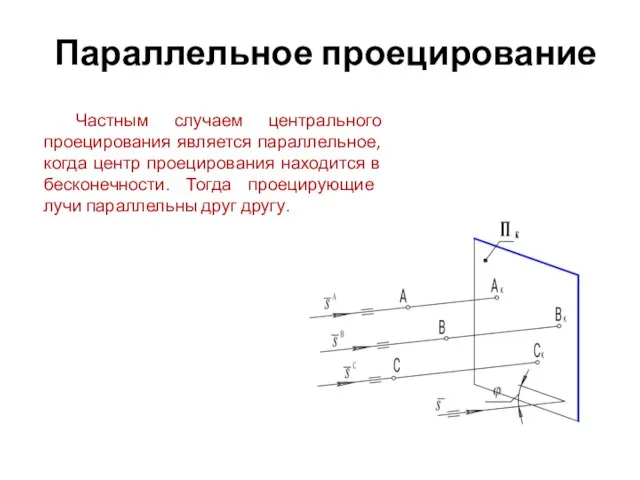
- 3. Параллельное проецирование Частным случаем центрального проецирования является параллельное, когда центр проецирования находится в бесконечности. Тогда проецирующие
- 4. Метод параллельного проецирования является основным при составлении чертежей зданий и сооружений. Гаспар Монж предложил проецировать все
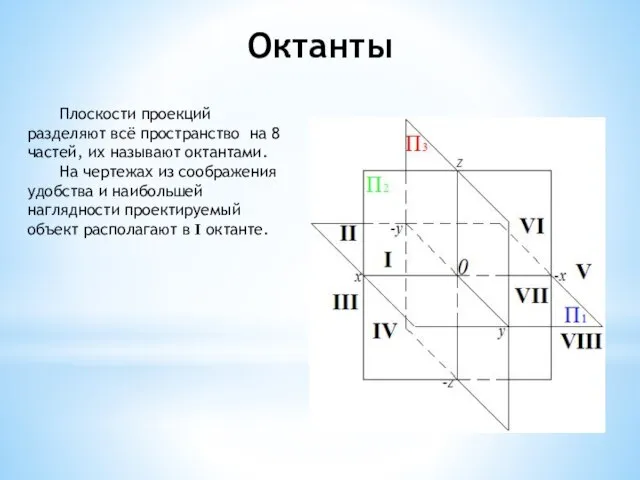
- 5. Октанты Плоскости проекций разделяют всё пространство на 8 частей, их называют октантами. На чертежах из соображения
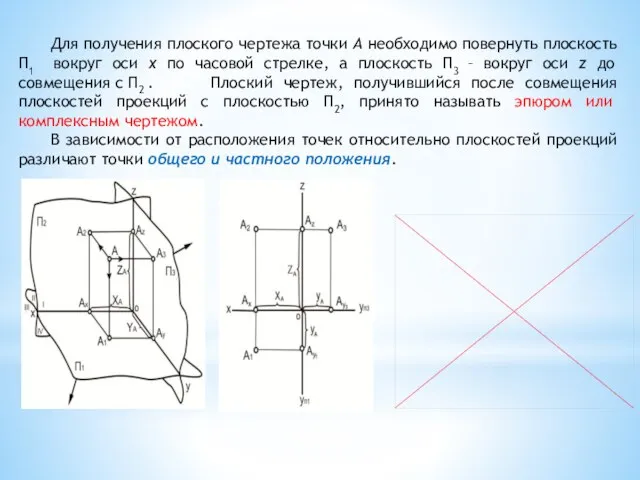
- 6. Для получения плоского чертежа точки А необходимо повернуть плоскость П1 вокруг оси x по часовой стрелке,
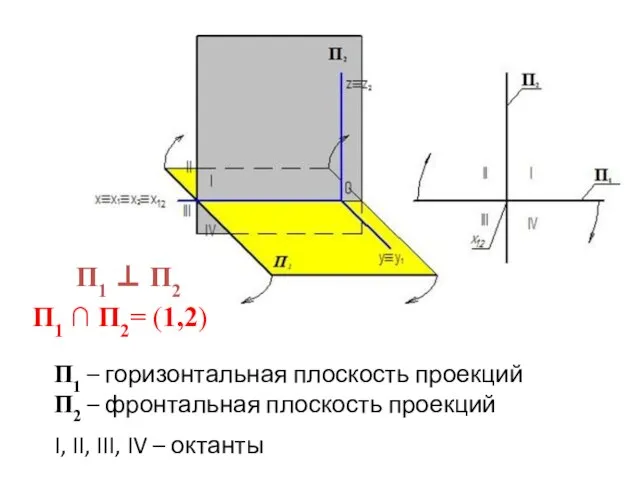
- 8. Ортогональная система двух плоскостей проекций
- 9. П1 ⊥ П2 П1 ∩ П2= (1,2) П1 – горизонтальная плоскость проекций П2 – фронтальная плоскость
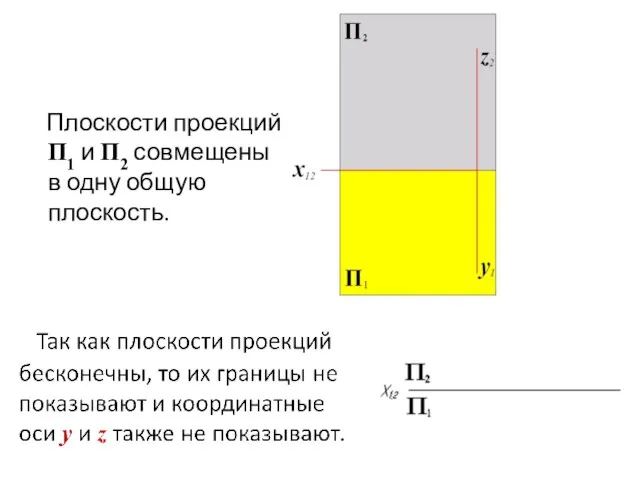
- 10. Плоскости проекций П1 и П2 совмещены в одну общую плоскость.
- 11. Проецирование точки
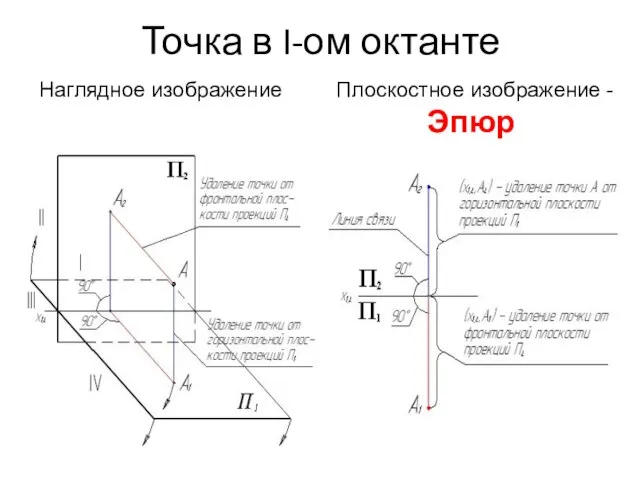
- 12. Точка в I-ом октанте Наглядное изображение Плоскостное изображение - Эпюр
- 14. Скачать презентацию



 А.Е. Суворов «Об итогах деятельности радиоэлектронного комплекса в 2007 году и основных задачах на 2008 год»
А.Е. Суворов «Об итогах деятельности радиоэлектронного комплекса в 2007 году и основных задачах на 2008 год» Сложение и вычитание натуральных чисел (5 класс)
Сложение и вычитание натуральных чисел (5 класс) Экономика и ее роль в жизни общества
Экономика и ее роль в жизни общества Игра-конкурс по информатике(2-4классы)
Игра-конкурс по информатике(2-4классы) Отдел контроля качества. ОКК ЕвроАвто
Отдел контроля качества. ОКК ЕвроАвто Мой край родной
Мой край родной Поезд в Пушкинские горы. Проект создания трансферного узла
Поезд в Пушкинские горы. Проект создания трансферного узла Ремёсла в России 17 – 18 вв
Ремёсла в России 17 – 18 вв Рассматриваемые вопросы Основы системного подхода Понятие предметной области (ПрО). Программа как модель ПрО Классы в Java: описание
Рассматриваемые вопросы Основы системного подхода Понятие предметной области (ПрО). Программа как модель ПрО Классы в Java: описание Из опыта работы методиста Томского областного института повышения квалификации и переподготовки работников образования
Из опыта работы методиста Томского областного института повышения квалификации и переподготовки работников образования Презентация на тему Простое осложнённое предложение
Презентация на тему Простое осложнённое предложение Родительское собрание : методика подготовки и проведения
Родительское собрание : методика подготовки и проведения Габдулла Тукай – Величайший татарский поэт
Габдулла Тукай – Величайший татарский поэт Семейство Лилейные
Семейство Лилейные Презентация на тему Художники 18 века
Презентация на тему Художники 18 века  Email рассылки в вашем магазине. Советы и примеры использования для решения задач.
Email рассылки в вашем магазине. Советы и примеры использования для решения задач. Оценка соответствия и особенности обращения продукции на территории таможенного союза Е.Петросян
Оценка соответствия и особенности обращения продукции на территории таможенного союза Е.Петросян Возможности электронного документооборота по управлению рисками
Возможности электронного документооборота по управлению рисками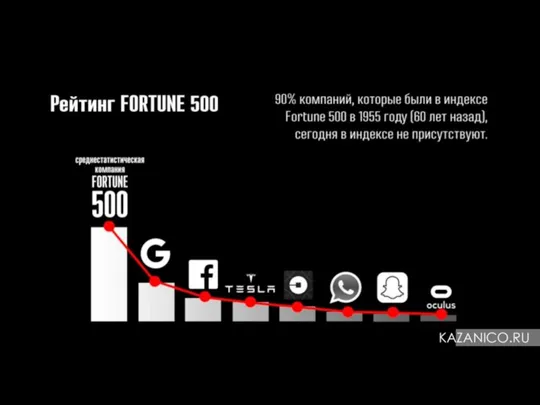 Рейтинг Fortune 5000
Рейтинг Fortune 5000 Закон О предотвращении эмиграции высококачественных z специалистов
Закон О предотвращении эмиграции высококачественных z специалистов Основные вопросы политической сферы
Основные вопросы политической сферы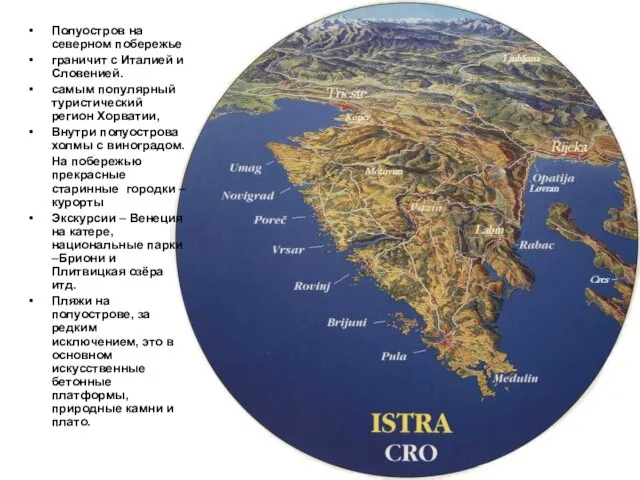 ИСТРА
ИСТРА Расписные военные тарелки Императорского фарфорового завода
Расписные военные тарелки Императорского фарфорового завода Vocabulary. Describing houses and homes
Vocabulary. Describing houses and homes Федеральный государственный образовательный стандарт дошкольного образования от 17.10.2013 № 1155
Федеральный государственный образовательный стандарт дошкольного образования от 17.10.2013 № 1155 Проекты, которые меняют страну к лучшему
Проекты, которые меняют страну к лучшему Загадки Даля
Загадки Даля Биофизика
Биофизика