Методы решения текстовых задач

Содержание:
Введение 3
1. Составные части задачи и требования по ее решению в школьном
курсе математики 4
2.Метод математического моделирования при решении текстовых задач. 6
2.1. Понятие модели и моделирования. 6
2.2. Моделирование при решении задач. 10
2.2.1.Задачи на встречное движение двух тел. 13
2.2.2.Задачи на движение двух тел в одном направлении. 14
2.2.3.Задачи на движение двух тел в противоположных направлениях. 15
2.3.Опытно-практическая работа по сопоставлению применяемых
способов решения задач в 5 и 9 классов. 17
Заключение 18
Приложение.
Список литературы.

Методы решения задач
- анализ и синтез
- метод сведения к ранее решённым
- метод математического
моделировавния
- метод математической индукции
- метод исчерпывающих проб

Метод математического моделирования
«В процессе математического моделирования выделяют три этапа:
1. Формализация – перевод предложенной задачи (ситуации) на язык
математической теории (построение математической модели задачи).
2. Решение задачи в рамках математической теории (говорят: решение внутри модели).
3.Перевод результата математического решения задачи на тот язык, на котором была сформулирована исходная задача (интерпретация решения).»

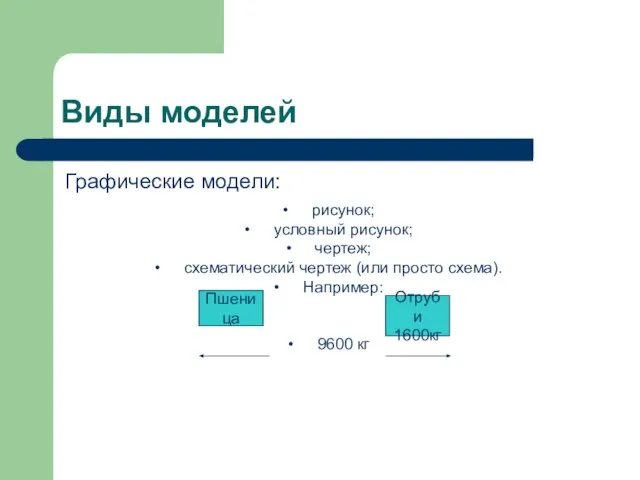
Виды моделей
Графические модели:
рисунок;
условный рисунок;
чертеж;
схематический чертеж (или просто схема).
Например:
9600 кг
Пшеница
Отруби
1600кг

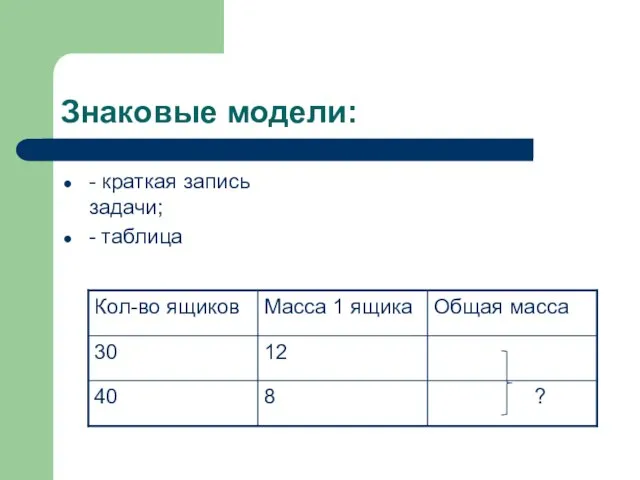
Знаковые модели:
- краткая запись задачи;
- таблица

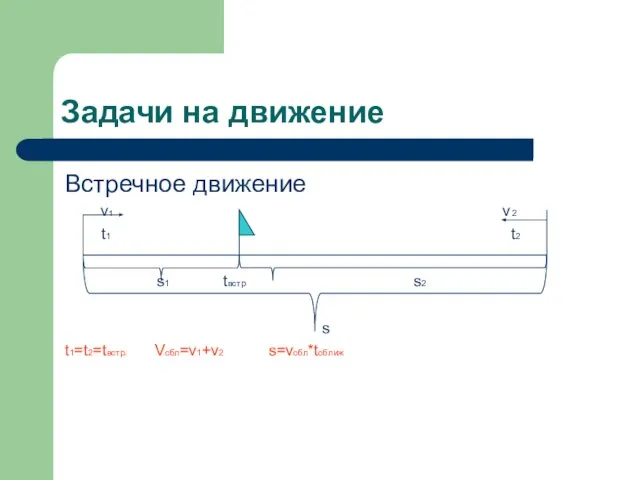
Задачи на движение
Встречное движение
v1 v2
t1 t2
s1 tвстр s2
s
t1=t2=tвстр. Vсбл=v1+v2 s=vсбл*tсближ

Движение в одном направлении
v1 v2
t1 t2
s s2
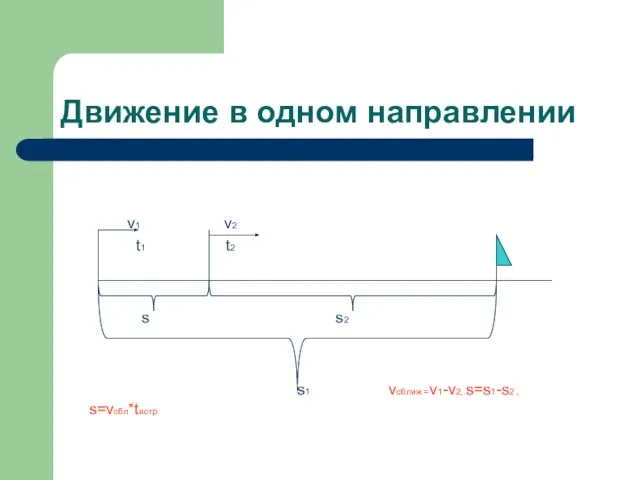
s1 vсближ =v1-v2,.s=s1-s2 , s=vсбл*tвстр

Движение в противоположных направлениях
В таких задачах два тела могут начинать движение в противоположных направлениях из одной точки:
а) одновременно;
б) в разное время.
А могут начинать свое движение из двух разных точек, находящихся на заданном расстоянии, и в разное время.
Общим теоретическим положением для них будет следующее:
v удал. = v1+ v2, где v1 и v2 соответственно скорости первого и второго тел.
(Схематический чертеж строится аналогично предыдущим).