Слайд 2 При радиометеорологическом зондировании атмосферы с помощью метеорологических радиолокационных станций (МРЛ) могут использоваться:
-

одноволновой метод,
- двухволновой метод.
Слайд 3Одноволновой
метод
радиолокационного зондирования атмосферы

Слайд 4
Одноволновой метод - это такая схема проведения активного дистанционного радиолокационного зондирования, при

котором МРЛ генерирует и регистрирует электромагнитное излучение строго на одной длине волны.
Этот метод зондирования основывается на измерении радиолокационной отражаемости метеорологических объектов.
Слайд 5 В основе одноволнового метода лежит использование уравнения дальности радиолокационного наблюдения метеорологических объектов.

Это же уравнение носит название основного уравнения радиолокации метеорологических объектов.
Основное уравнение радиолокации метеорологических объектов связывает между собой:
- технические характеристики используемой РЛС,
- характеристики метеорологических объектов, определяющие их отражающие свойства,
- возможную дальность обнаружения метеорологических объектов.
Слайд 6 Вывод основного уравнения радиолокации метеорологических объектов проведем для:
- моностатической радиолокационной системы, когда
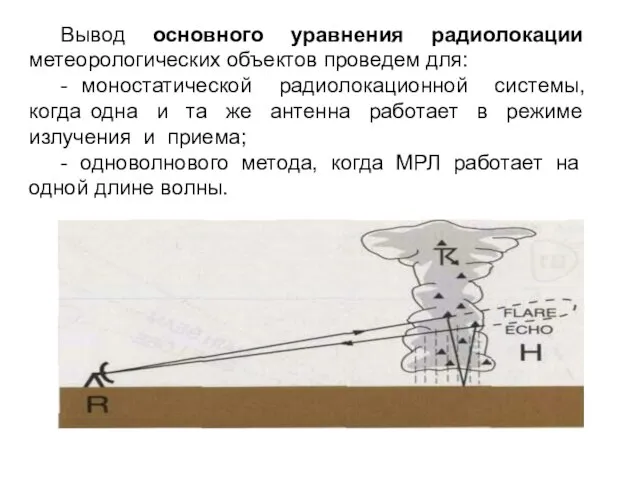
одна и та же антенна работает в режиме излучения и приема;
- одноволнового метода, когда МРЛ работает на одной длине волны.
Слайд 7
Часть 1.
Одиночная цель - отдельная частица

Слайд 8 Рассмотрим при ряде упрощающих предположений формирование регистрируемого МРЛ ответного сигнала, рассеянного от

отдельной частицы с известной эффективной площадью рассеяния Ϭ, находящейся на расстоянии R от радиолокатора с антенной диаметром D.
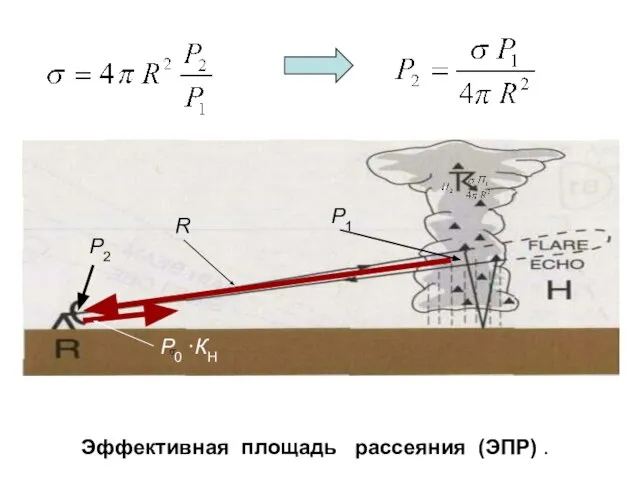
При этом напомним, что эффективная площадь рассеяния частицы σ равна
где
Р1 - плотности потоков мощности электромагнитной волны в точке расположения частицы;
Р2 - плотности потоков мощности рассеянной электромагнитной волны в точке расположения МРЛ;
R - расстояние от МРЛ до частицы.
Слайд 9R
Р1
Р2
Эффективная площадь рассеяния (ЭПР) .
Р0 ·КН
Слайд 10 Пусть Р1 - плотность потока мощности электромагнитной волны от МРЛ в точке

нахождения частицы. Если обозначить P0 – мощность передатчика МРЛ и Кн – коэффициент направленного действия антенны, то для Р1 в точке, находящейся на расстоянии R от МРЛ можно записать
По определению эффективной площади рассеяния Ϭ от пришедшего импульса общее количество рассеянной во все стороны от частицы энергии будет равно
Ϭ ·Р1 .
Слайд 11
При равномерном рассеянии во все стороны вся эта энергия равномерно распространиться по

поверхности сферы, площадь которой в точке расположения МРЛ будет равна 4π R2. При этом на единицу площади будет приходиться поток излучения, равный
Ϭ ·Р1 / (4π R2).
Слайд 12 При диаметре антенны D площадь её поверхности будет равна π·D2/4. Следовательно, общее

количество энергии P2, принятой антенной, будет равно
где
σ − эффективная площадь рассеяния (ЭПР) частицы метеорологической цели,
D − диаметр антенны,
Р1 − плотности потока мощности падающей (в точке расположения частицы) электромагнитной энергии,
R − расстояние от МРЛ до частицы.
Слайд 13 Здесь приняты два упрощения.
Первое упрощение - чтобы получить поток излучения на

антенну, необходимо, вообще говоря, проинтегрировать сигнал по площади раскрыва антенны в пределах телесного угла, под которым видна цель. Учитывая, что при радиолокации метеорологических целей этот телесный угол весьма мал, можно пренебречь зависимостью ЭПР метеоцели от направления, под которым она просматривается, и заменить интегрирование умножением плотности потока мощности на величину площади раскрытия антенны.
Второе упрощение связано с заменой эффективного диаметра антенны геометрическим.
Слайд 14 С учетом введенного ранее определения мощности передатчика Р0 и коэффициента направленного действия

антенны в режиме излучения (Kн) выражение для Р1 можно переписать в следующем виде
где, как было показано ранее, в приближении Релеевского рассеяния
Слайд 15
R
Антенна
Облучатель
Частица (цель)
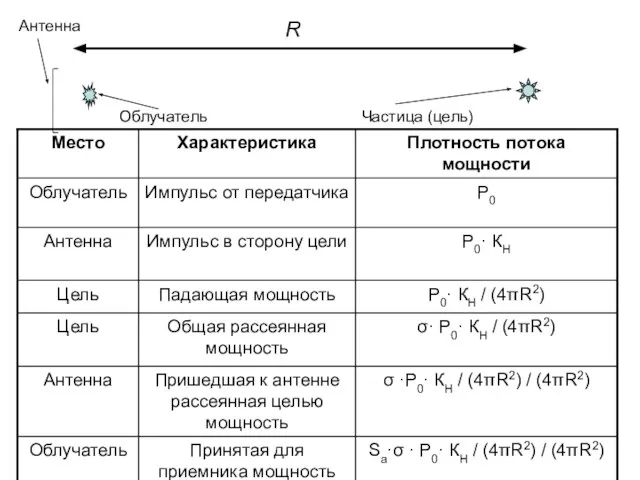
Слайд 16 При этом одиночная цель может быть обнаружена, если информационный сигнал P1 надежно

выделяется как на фоне сигналов от других целей, так и на фоне собственных шумов МРЛ: Рш
где kp > 1 и
Слайд 17
Часть 2.
Пространственно-распределенные метеорологические цели - ансамбль частиц

Слайд 18 Чтобы получить мощность отраженного сигнала (радиоэха) от ансамбля частиц, представляющих метеорологический объект,

необходимо просуммировать информационные сигналы от всех частиц, расположенных в импульсном отражающем объеме метеорологического объекта Vи , который может быть определен с помощью соотношения
где
− длительность зондирующего импульса,
с − скорость распространения электромагнитной энергии в атмосфере,
θ − ширина диаграммы направленности антенны МРЛ.
Слайд 19
Например, если
R = 40 км, θ = 0,5, τ = 1

мкс,
то отражающий объем в облаке будет равен 1,43×107 м3, а эхосигнал будет создаваться 1010 частицами (при средней концентрации – несколько сотен частиц в 1 м3).
Слайд 20 В этом случае величина отраженного сигнала (радиоэха) будет определяться следующим выражением
где

- плотности потоков мощности электромагнитной волны в точке расположения i-ой частицы, а интегрирование (суммирование) ведется по всему ансамблю частиц с различными значениями σi , заключенных в импульсным отражающим объемом Vu.
Для получения зависимости Рп от удельной ЭПР η разложим функцию Р1(Ϭi) в ряд Тейлора
Слайд 21
Теперь положим, что и Ϭ0 = 0 и учтем (как было показано

ранее для одной частицы), что
Тогда
и, следовательно, не зависит от Ϭ i
Слайд 22 Тогда учитывая, что по определению
для Рп получаем
Здесь учтено, что не зависит

от Ϭi и, следовательно,
может быть вынесено за знак интеграла, а так же тот факт, что Р1(Ϭ0) = 0.
Слайд 23
Подставив вместо и Vи соответствующие
выражения, получаем уравнение радиолокации пространственно распределенного

метеорологического объекта:
Слайд 24
В метеорологических РЛС, как правило, применяются антенны с осесимметричными диаграммами направленности.

Для антенны с осесимметричными диаграммами направленности коэффициент направленного действия с шириной диаграммы направленности θ можно приближенно считать, чтo
Kн ≈ 16 /θ2 .
Слайд 25 Подставляя последнее соотношение в уравнение радиолокации пространственно распределенного метеорологического объекта, получаем:

Если ввести постоянную радиолокатора CРЛ:
то уравнение радиолокации пространственно распределенного метеорологического объекта теперь можно записать следующим образом:
.
Здесь Рп – поток излучения , сформированный импульсным отражающим объемом, Р0 – импульсная мощность передатчика РЛС.
Слайд 26 В уравнение радиолокации метеорологических объектов наряду со значением Рп – потоком излучения,

сформированного импульсным отражающим объемом и значением Р0 – импульсной мощностью передатчика РЛС можно ввести мощность собственных шумов приемника радиолокатора Pш.
Тогда уравнение радиолокации метеорологических объектов будет иметь следующий удобный для практического применения вид
где
В таком варианте в левой части уравнение радиолокации метеорологических объектов оказывается величина превышения полезного сигнала над уровнем собственных шумов РЛС.
Слайд 27 Ранее было показано что удельная ЭПР метеорологического объекта η при релеевском типе

рассеяния электромагнитной энергии (размер частиц существенно меньше длины волны) может быть определена из соотношения
Кроме того, ранее было введено значение радиолокационной отражаемости Za, определяемое следующим соотношением
где суммирование ведется по всем частицам, содержащихся в импульсном объеме.
Слайд 28 Если ввести функцию распределения капель по размерам в импульсном объеме N(a), то

для функции Za можно записать
где a – диаметр частицы.
Для монодисперсного распределения отражающих частиц внутри импульсного объема радиолокационная отражаемость будет определяться следующим выражением
где N – количество частиц в единице объема, а – диаметр частиц, m – комплексная диэлектрическая проницаемость материала частиц.
Слайд 29
Тогда для удельной эффективной площади рассеяния (удельной ЭПР) можно записать
где λ –

длина волны,
Za - радиолокационная отражаемость.
Слайд 30 Объединив выражения для удельной эффективной площади рассеяния единицы объема η
и
окончательно

получаем:
где
Слайд 31
Величина Прл носит название метеорологического потенциала МРЛ. Потенциал РЛС определяется только
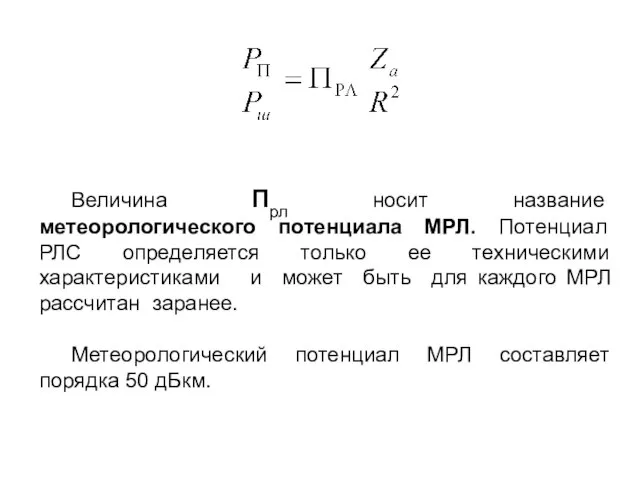
ее техническими характеристиками и может быть для каждого МРЛ рассчитан заранее.
Метеорологический потенциал МРЛ составляет порядка 50 дБкм.
Слайд 32
Для облаков характерный диапазон значений Za - радиолокационная отражаемость, может изменяться

на 12 порядков. При этом величина Zа варьирует в интервале от 105 мм6/м3 до 10-7 мм6/м3. Поэтому на практике вместо Zа обычно используют либо величину lgZа, либо другую единицу – децибелл:
dБZа = 10·(lgZа/lgZ0), (3),
где Z0 = 1мм6/м3.
Слайд 33 Таким образом, основное уравнение радиолокации метеорологических целей принимает следующий вид:
Здесь

Рп – потоком излучения, сформированного импульсным отражающим объемом, находящимся на расстоянии R от РЛС,
Pш - мощность собственных шумов радиолокатора,
Прл - метеорологический потенциал РЛС,
Za – радиолокационная отражаемость.
Выведенное уравнение позволяют по величине измеренного отраженного сигнала Рп определить отражаемость метеорологического объекта Za, находящегося на расстоянии R от МРЛ.
Слайд 34 Величины, входящие в основное уравнение радиолокации метеорологических целей имеют следующие размерности:
-

метеорологического потенциала МРЛ Прл измеряется в км2/(мм6/м3);
- расстояние R от МРЛ измеряется в км;
- радиолокационная отражаемость Za измеряется в мм6/м3;
- мощности Рп и Pш измеряются в Вт.
Слайд 35 На практике основное уравнение радиолокации используется несколько в другом виде что,

соответственно, приводит к изменению размерностей входящих в него величин.
Для получения такой используемой на практике формы прологарифмируем основное уравнение радиолокации метеорологических целей и умножим левую и правую части полученного выражения на 10. Тогда рабочий вид основного уравнения радиолокации метеорологических целей можно записать следующим образом:
где
Размерности двух последних величин (с апострофами) – децибеллы (дБ).
Слайд 36 Сравнивая два выражения: уравнение радиолокации точечной цели и уравнение радиолокационного наблюдения

пространственно-распределенной цели, можно заметить, что:
- при радиолокационном наблюдении точечной цели величина отраженного сигнала обратно пропорциональна четвертой степени расстояния от МРЛ,
- при радиолокационном наблюдении пространственно-распределенной цели величина отраженного сигнала обратно пропорциональна второй степени корню расстояния от МРЛ.
Такая особенность обусловлена различиями в зависимости эффективной площади рассеяния (ЭПР) точечных и пространственно-распределенных метеорологических объектов от расстояния.
Слайд 37 Здесь важно отметить, что поскольку метеорологические объекты обладают разной отражаемостью и, более

того, даже один метеорологический объект может иметь достаточно сложное распределение отражаемости в вертикальном и горизонтальном направлениях, выведенные уравнения определяют возможность получения ряда дополнительных характеристик метеорологических объектов.
К таким дополнительным характеристикам метеорологических объектов, в частности, относятся:
- вертикальный профиль отражаемости,
- горизонтальные и горизонтальные размеры метеорологических объектов,
- пространственные и временные градиенты отражаемости,
- высоты верхней и нижней границ облачности.
Слайд 38Двухволновой
метод
радиолокационного зондирования атмосферы

Слайд 39
Большими возможностями обладает двухволновой метод радиометеорологического зондирования атмосферы. В этом случае зондирование

производится с использованием электромагнитного излучения на двух длинах волн.
В двухволновом методе отсутствуют те недостатки, которые присущи одноволновому методу. Однако появляются существенные трудности в его технической реализации. Более широкое развитие этот метод получил при реализации лидарного зондирования атмосферы.
Слайд 40 Двухволновой метод основывается на различиях в частотной зависимости характеристик рассеяния электромагнитных волн

гидрометеорами различных размеров.
Этот метод разработан в результате обширных теоретических исследований закономерностей рассеяния электромагнитных волн СВЧ диапазона (сантиметровых) встречающихся в облаках и осадках моделями спектров различных гидрометеоров (капли, градины, крупа, снег) и экспериментальных многоволновых радиолокационных исследований метеорологических объектов.
Слайд 41 Двухволновый метод основан на том, что в мелкодисперсных осадках независимо от их

интенсивности отношение отражаемости для длин волн λ1 = 3,2 и λ2 = 10 см равно , а с укрупнением града уменьшается в 10 - 100 раз.
Этот метод обеспечивает распознавание градовых облаков и измерение размера и кинетической энергии града (при условии введения коррекции на ослабление 3,2 см излучения в осадках).
Слайд 42 Практическая реализация двухволнового метода исследования метеорологических объектов требует:
- проведения одновременных и пространственно-совмещенных

измерений эффективной площади рассеивания единичного объема с помощью двух МРЛ, работающих на двух различающихся между собой длинах волн,
- непосредственного измерения отношения эффективных площадей рассеивания единичного объема с помощью одного двухволнового МРЛ, имеющего одинаковую ширину диаграммы направленности на длинах волн λ1 и λ2 и синхронизированные по времени длительности зондирующих импульсов по обоим каналам.
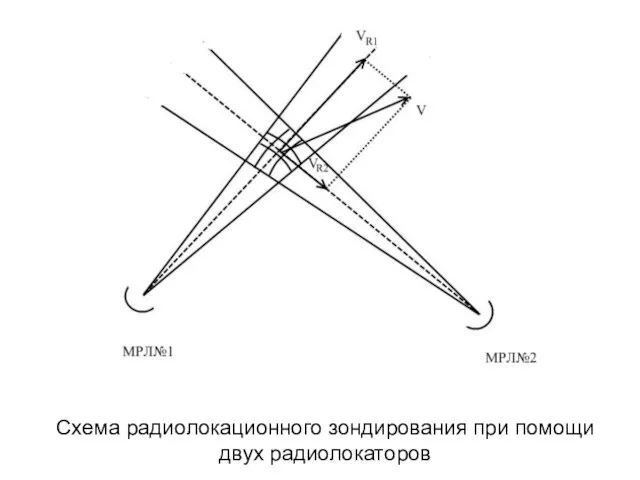
Слайд 43
Схема радиолокационного зондирования при помощи двух радиолокаторов
Слайд 44 Двухволновой метод основывается на различиях в частотной зависимости рассеяния электромагнитных волн гидрометеорами

различных размеров.
Двухволновой метод базируется:
- на результатах обширных теоретических исследований закономерностей рассеяния электромагнитных волн СВЧ диапазона (сантиметровых) встречающихся в облаках и осадках моделями спектров различных гидрометеоров (капли, градины, крупа, снег);
- на результатах, полученных на основе экспериментальных исследований взаимодействия метеорологических объектов с электромагнитным излучение в радиодиапазоне.
Слайд 45 В случае малых сферических частиц, где возможно применение релеевского типа рассеяния отношение

отражаемостей на двух длинах волн является в первом приближении однозначной функцией размера рассеивающих частиц, т.е.
= сonst.
где η - эффективной площади рассеяния единицы объема на длине волны λ.
Это выражение называется уравнением двухволновой радиолокации и является справедливым практически для любых гидрометеоров, так как влияние их диэлектрических свойств на величину отражаемости в случае малых частиц оказывается несущественным.
Слайд 47Рядом Тейлора для функции f(x) в окрестности точки a называется степенной ряд

относительно двучлена (x - a) следующего вида:
Слайд 48Метеорологический потенциал МРЛ-5 составляет порядка 50 дБкм, для ДМРЛ С-диапазона метеорологический потенциал

в режиме регистрации отраженного сигнала равен 57 дБкм, в доплеровском режиме составляет 65 дБкм.















































 Презентация на тему Повторение о глаголе
Презентация на тему Повторение о глаголе Алгоритмы сортировки
Алгоритмы сортировки Всемирный Банк и МолодежьThe Young Professionals Program
Всемирный Банк и МолодежьThe Young Professionals Program Построение корпоративной системы риск-менеджмента
Построение корпоративной системы риск-менеджмента Презентация на тему амфотерные оксиды и гидроксиды
Презентация на тему амфотерные оксиды и гидроксиды  Реформы государственного управления при Петре I
Реформы государственного управления при Петре I Соучастие в преступлении
Соучастие в преступлении Гидродинамические аварии
Гидродинамические аварии Урок по лыжной подготовке в 4-м классе
Урок по лыжной подготовке в 4-м классе Презентация на тему Поздравление ветеранов с праздником Победы
Презентация на тему Поздравление ветеранов с праздником Победы  Prakticheskaya_rabota_2
Prakticheskaya_rabota_2 Блюда студенческой столовой
Блюда студенческой столовой Понедельник - день тяжелый?
Понедельник - день тяжелый? Инструкция для родителей по подаче заявления о зачислении в образовательную организацию
Инструкция для родителей по подаче заявления о зачислении в образовательную организацию Международные организации. 10 класс
Международные организации. 10 класс Презентация на тему Типы молодежных субкультур
Презентация на тему Типы молодежных субкультур Пожарный проводной комплекс аудио связи ППК-АС
Пожарный проводной комплекс аудио связи ППК-АС «Семейная тема в произведениях А.С. Пушкина «Дубровский» и «Барышня-Крестьянка».
«Семейная тема в произведениях А.С. Пушкина «Дубровский» и «Барышня-Крестьянка». Сети ЭВМ и телекоммуникации
Сети ЭВМ и телекоммуникации Автоматизация звук ш
Автоматизация звук ш Деление числа, оканчивающегося нулями
Деление числа, оканчивающегося нулями ВНЕДРЕНИЕ СТАНДАРТОВ МЕДИЦИНСКОЙ ПОМОЩИ В ХОДЕ РЕАЛИЗАЦИИ РЕГИОНАЛЬНЫХ ПРОГРАММ МОДЕРНИЗАЦИИ ЗДРАВООХРАНЕНИЯ
ВНЕДРЕНИЕ СТАНДАРТОВ МЕДИЦИНСКОЙ ПОМОЩИ В ХОДЕ РЕАЛИЗАЦИИ РЕГИОНАЛЬНЫХ ПРОГРАММ МОДЕРНИЗАЦИИ ЗДРАВООХРАНЕНИЯ Культурная ассимиляция и формирование ценностей, потребление предметов искусства и культуры
Культурная ассимиляция и формирование ценностей, потребление предметов искусства и культуры МОУ Тальянская СОШ
МОУ Тальянская СОШ Презентация на тему Электронные библиотеки
Презентация на тему Электронные библиотеки Региональный опыт построения электронногоправительства в Амурской области
Региональный опыт построения электронногоправительства в Амурской области Внешнее строение листа
Внешнее строение листа Презентация на тему Законы Ньютона (10 класс)
Презентация на тему Законы Ньютона (10 класс)