Содержание
- 2. Микропроцессоры кардинально изменили наш мир Сотовые телефоны, интернет, достижения в медицинской сфере Объем продаж полупроводниковой промышленности
- 3. Цель курса: Понять, что происходит внутри корпуса компьютера Изучить оснвоные принципы цифровой схемотехники Научиться разрабатывать проекты
- 4. Абстракция Дисциплина Три базовых принципа Иерархичность Модульность Регулярность Искусство управления сложностью
- 5. Исключение из рассмотрения деталей, которые в данном контексте неважны Абстракция
- 6. Намеренное ограничение выбора возможных проектных решений Пример: Цифровая дисциплина Использование дискретных значений напряжений вместо непрерывных Цифровые
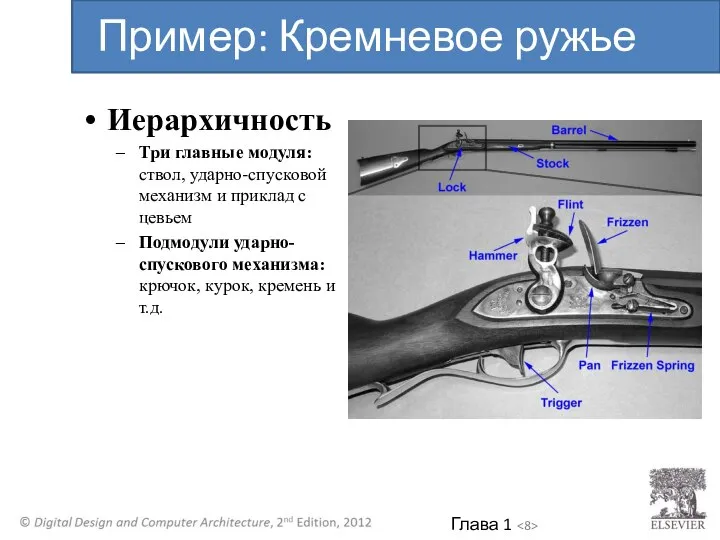
- 7. Иерархичность Система разделяется на модули и подмодули Модульность Каждый модуль имеет четко определенные функции и интерфейсы
- 8. Иерархичность Три главные модуля: ствол, ударно-спусковой механизм и приклад с цевьем Подмодули ударно-спускового механизма: крючок, курок,
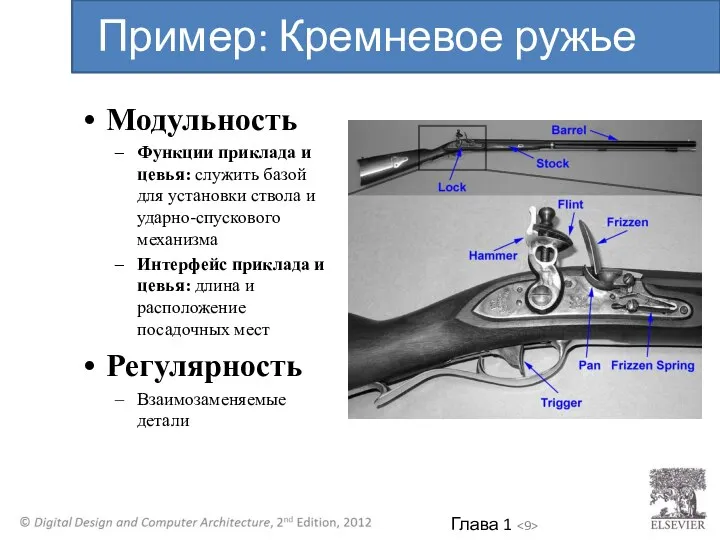
- 9. Модульность Функции приклада и цевья: служить базой для установки ствола и ударно-спускового механизма Интерфейс приклада и
- 10. Большинство физических величин непрерывны Потенциал проводника Частота колебаний Положение тела Цифровая абстракция рассматривает дискретное множество возможных
- 11. Спроектирована Чарльзом Бэббиджем в 1834 – 1871 годах Считается первым цифровым компьютером Построена из механических шестеренок,
- 12. Два дискретные значения: 1 и 0 1, Истина, Большая величина 0, Ложь, Малая величина 1 и
- 13. Родился в семье небогатого ремесленника Самостоятельно изучал математику и стал преподавателем Королевского колледжа в Ирландии. Написал
- 14. Десятичные числа Двоичные числа Системы счисления
- 15. Десятичные числа Двоичные числа Системы счисления
- 16. 20 = 21 = 22 = 23 = 24 = 25 = 26 = 27 =
- 17. 20 = 1 21 = 2 22 = 4 23 = 8 24 = 16 25
- 18. Преобразование двоичного числа в десятичное: Преобразовать 100112 в десятичное число Преобразование десятичного числа в двоичное: Преобразовать
- 19. Преобразование десятичного числа в двоичное: Преобразовать 100112 в десятичное число 16×1 + 8×0 + 4×0 +
- 20. N-разрядное десятичное число Сколько значений? Диапазон? Пример: Трехразрядное десятичное число N-битовое двоичное число Сколько значений? Диапазон:
- 21. N-разрядное десятичное число Сколько значений? 10N Диапазон? [0, 10N - 1] Пример: Трехразрядное десятичное число 103
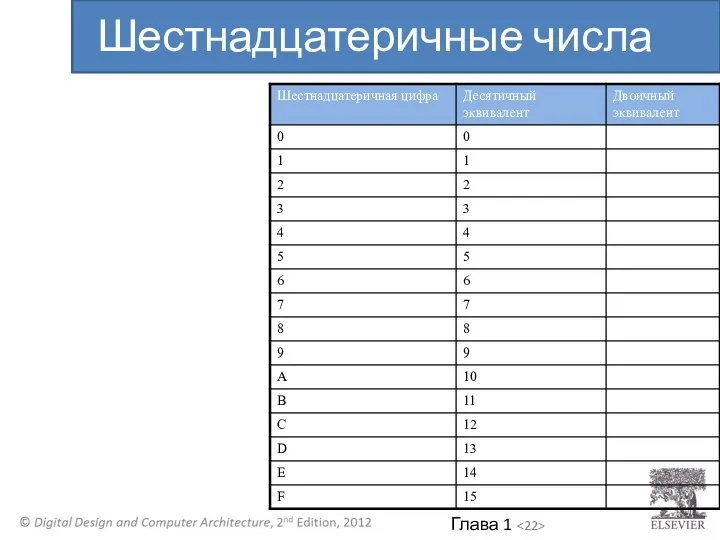
- 22. Шестнадцатеричные числа
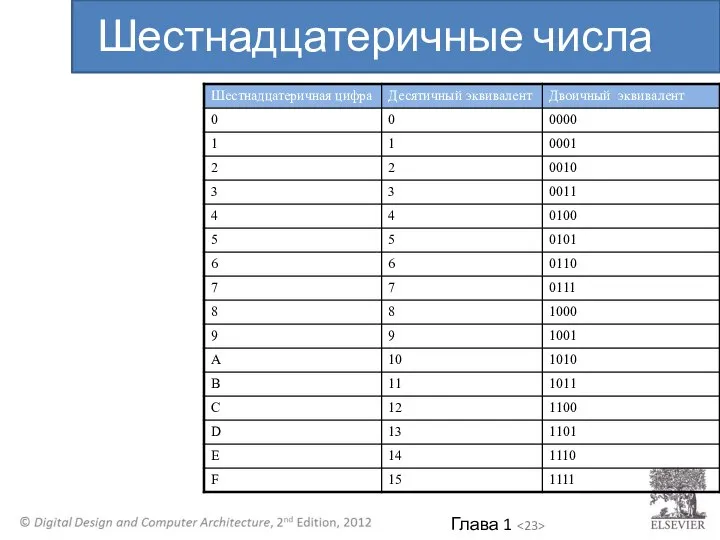
- 23. Шестнадцатеричные числа
- 24. Основание 16 Компактная запись двоичных чисел Шестнадцатеричные числа
- 25. Преобразование шестнадцатеричных чисел в двоичные: Преобразовать 4AF16 (также записывается 0x4AF) в двоичное число Преобразование шестнадцатеричных чисел
- 26. Преобразование шестнадцатеричных чисел в двоичные: Преобразовать 4AF16 (также записывается 0x4AF) в двоичное число 0100 1010 11112
- 27. Биты Байты и полубайты (nibble) Байты Биты, байты, полубайты...
- 28. 210 = 1 кило ≈ 1000 (1024) 220 = 1 мега ≈ 1 миллион (1,048,576) 230
- 29. Чему равно 224? Сколько значений может представить 32-битовая переменная? Вычисление степеней 2
- 30. Чему равно 224? - 24 × 220 ≈ 16 миллионов Сколько значений может представить 32-битовая переменная?
- 31. Десятичное Двоичное Сложение
- 32. Сложите следующие 4-битовые двоичные числа Сложите следующие 4-битовые двоичные числа Примеры сложения двоичных чисел
- 33. Сложите следующие 4-битовые двоичные числа Сложите следующие 4-битовые двоичные числа Переполнение! Примеры сложения двоичных чисел
- 34. Цифровые системы работают с фиксированным количеством разрядов Переполнение: когда результат слишком большой, чтобы поместится в доступном
- 35. Числа в прямом коде Числа в дополнительном коде Двоичные числа со знаком
- 36. Один знаковый бит, N-1 битов величины Знаковый бит является старшим (самым левым) битом Положительные числа: знаковый
- 37. Один знаковый бит, N-1 битов величины Знаковый бит является старшим (самым левым) битом Положительные числа: знаковый
- 38. Недостатки: Стандартный способ сложения не работает, например, -6 + 6: 1110 +0110 10100 (не правильно!) Два
- 39. Не имеет проблем прямого кода Алгоритм сложения работает Единственное представление 0 Числа в дополнительном коде
- 40. Старший бит имеет вес -2N-1 Наибольшее положительное 4-битовое число Наибольшее (по модулю) отрицательное 4-битовое число Старший
- 41. Старший бит имеет вес -2N-1 Наибольшее положительное 4-битовое число 0111 Наибольшее (по модулю) отрицательное 4-битовое число
- 42. Изменение знака числа, представленного в дополнительном коде Метод: Инвертировать биты Добавить 1 Пример: Изменить знак 310
- 43. Изменение знака числа, представленного в дополнительном коде Метод: Инвертировать биты Добавить 1 Пример: Изменить знак 310
- 44. Найти представление в дополнительном коде числа 610 = 01102 Чему равно десятичное представление числа 10012? Примеры
- 45. Найти представление в дополнительном коде 610 = 01102 1001 + 1 1010 = -610 Чему равно
- 46. Сложить числа 6 + (-6) с использованием дополнительного кода Сложить числа -2 + 3 с использованием
- 47. Сложить числа 6 + (-6) с использованием дополнительного кода Сложить числа -2 + 3 с использованием
- 48. Copyright © 2012 Elsevier Увеличить количество бит с N до M (M > N) : Знаковое
- 49. Знаковый бит копируется во все новые старшие биты Значение числа не изменяется Пример 1: 4-битовое представление
- 50. Все новые старшие биты принимают нулевое значение Значение отрицательных чисел изменяется Пример 1: 4-битовая величина =
- 51. Пример: 4-битовое представление: Сравнение способов представления двоичных чисел
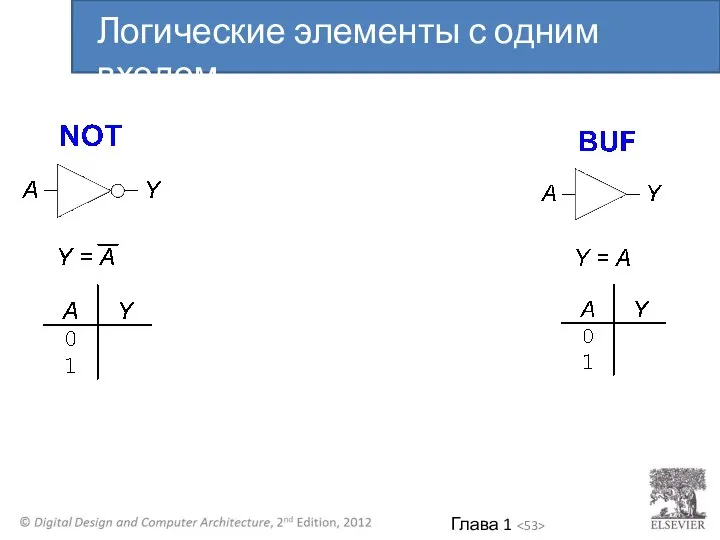
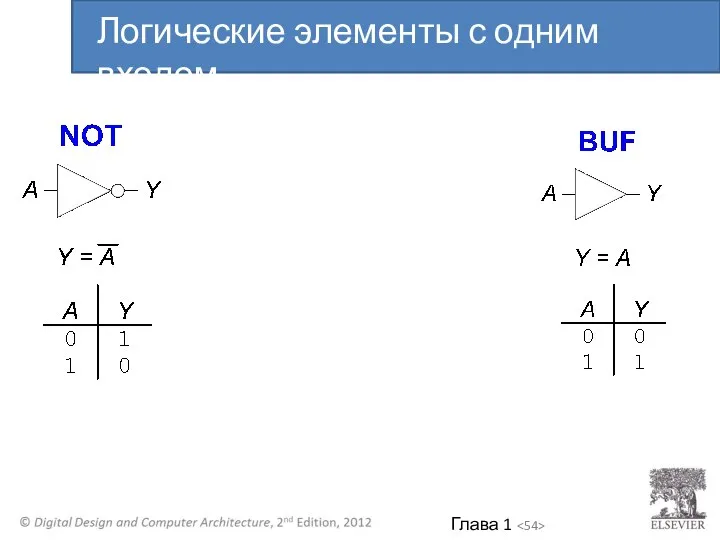
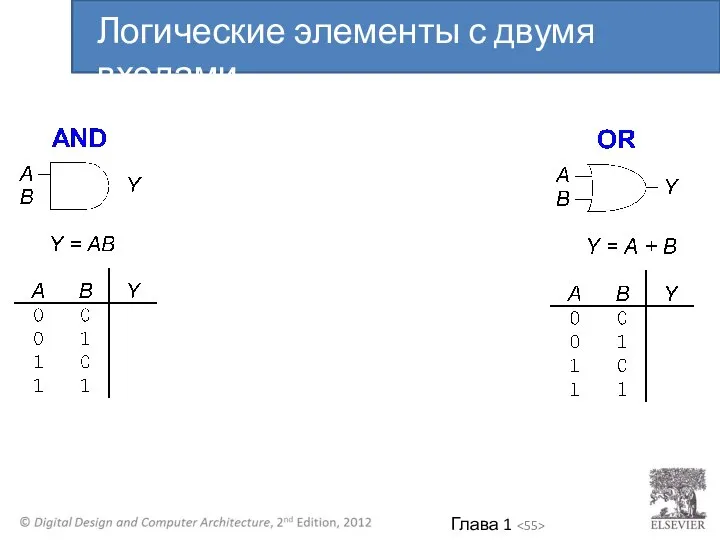
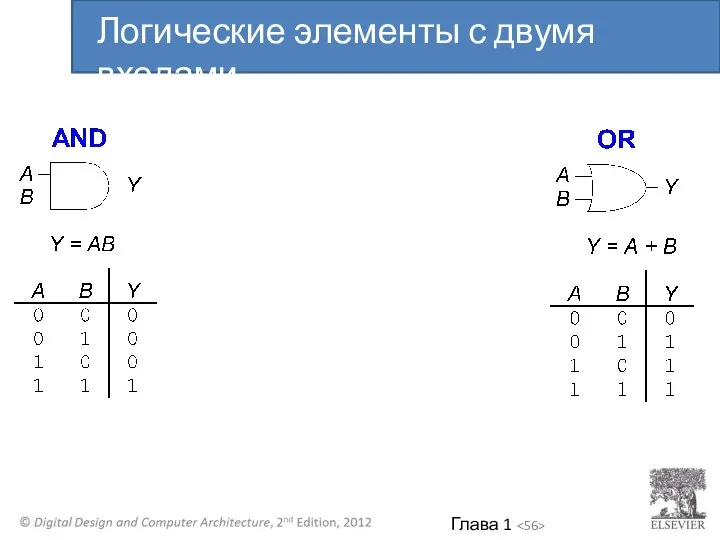
- 52. Выполняют логические функции Инверсия (НЕ), И (AND), ИЛИ (OR), И-НЕ(NAND), ИЛИ-НЕ(NOR), и т.д. С одним входом
- 53. Логические элементы с одним входом
- 54. Логические элементы с одним входом
- 55. Логические элементы с двумя входами
- 56. Логические элементы с двумя входами
- 57. Прочие логические элементы с двумя входами
- 58. Прочие логические элементы с двумя входами
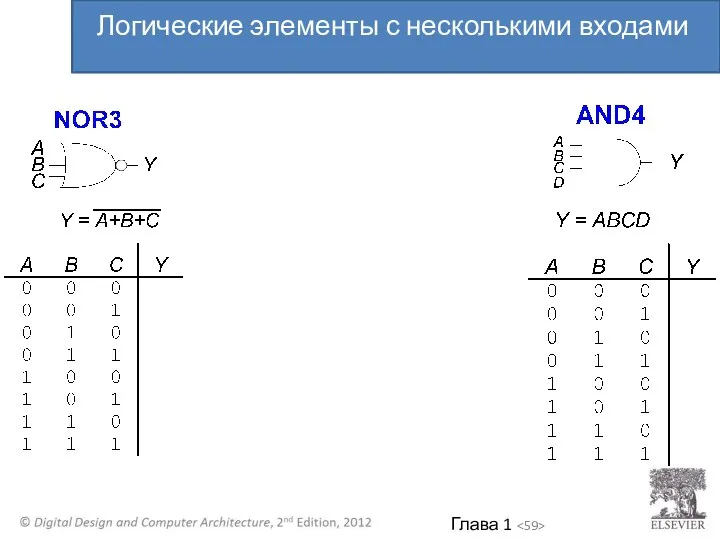
- 59. Логические элементы с несколькими входами
- 60. Многовходовый элемент XOR: Контроль четности Логические элементы с несколькими входами
- 61. Дискретные уровни напряжения представляют 1 и 0 Например: 0 = земля (GND) или 0 В 1
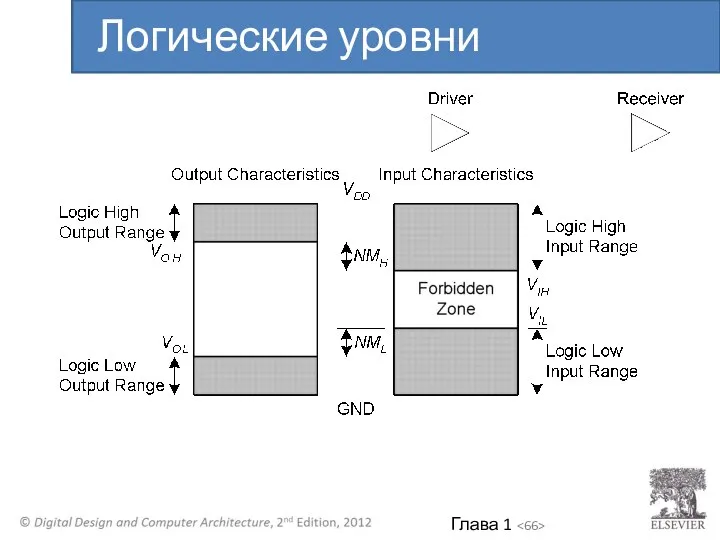
- 62. Диапазон напряжений для 1 и 0 Разные диапазоны для входов и выходов обеспечивают работу схем при
- 63. Что такое шум?
- 64. Любая помеха искажающая сигнал Например, сопротивление проводников, помехи источника питания, наводки от соседних проводников и т.д.
- 65. Если на вход элемента поступают корректные логические значения, на его выходе формируются корректные выходные сигналы Для
- 66. Логические уровни
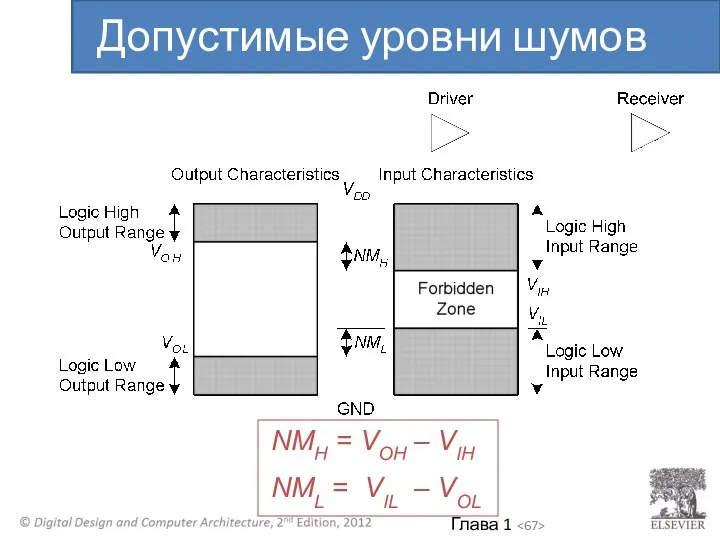
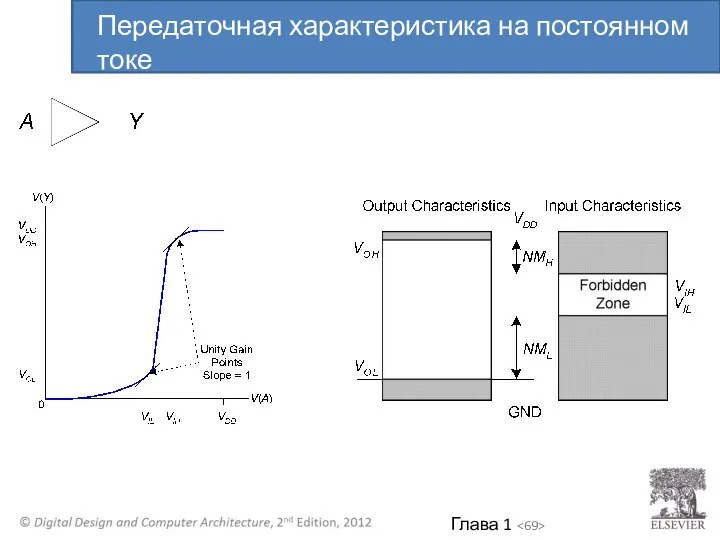
- 67. NMH = VOH – VIH NML = VIL – VOL Допустимые уровни шумов
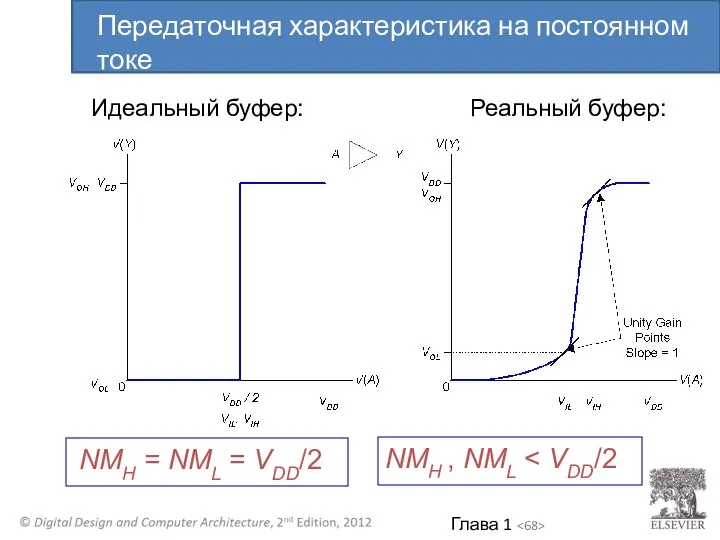
- 68. Идеальный буфер: Реальный буфер: NMH = NML = VDD/2 NMH , NML Передаточная характеристика на постоянном
- 69. Передаточная характеристика на постоянном токе
- 70. В 1970 и 1980 годы, VDD = 5 В В следующие годы VDD уменьшается Уменьшается нагрев
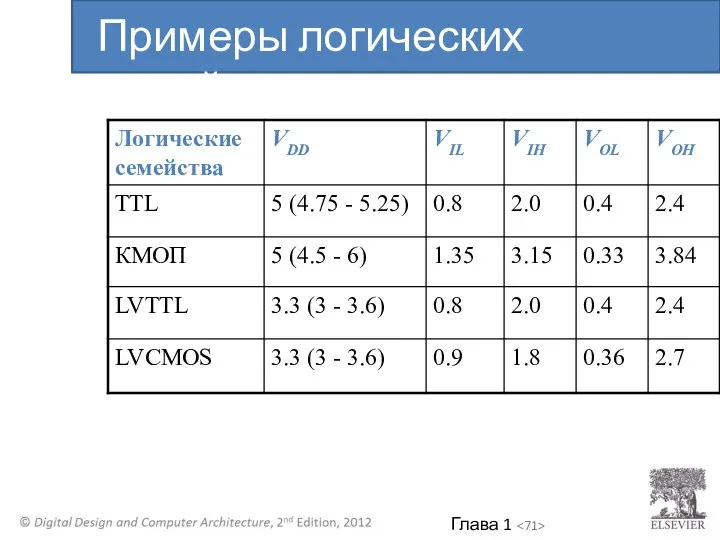
- 71. Примеры логических семейств
- 72. Логические элементы состоят из транзисторов Трехвходовый управляемый напряжением выключатель Соединение двух входов зависит от напряжения на
- 73. Прозвище - “Мэр Силиконовой долины” Со-основатель Fairchild Semiconductor в 1957 году Со-основатель Intel в 1968 году
- 74. Транзисторы создаются из полупроводникового материала, кремния Чистый кремний плохой проводник (свободные носители заряда отсутствуют) Легированный кремний
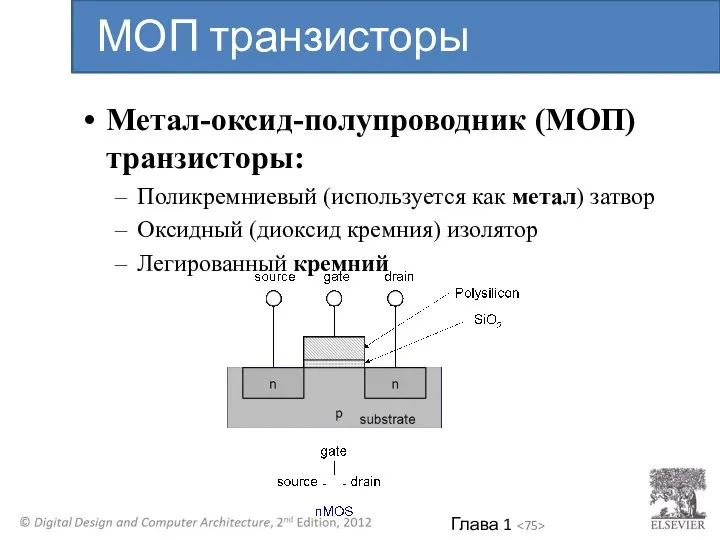
- 75. Метал-оксид-полупроводник (МОП) транзисторы: Поликремниевый (используется как метал) затвор Оксидный (диоксид кремния) изолятор Легированный кремний МОП транзисторы
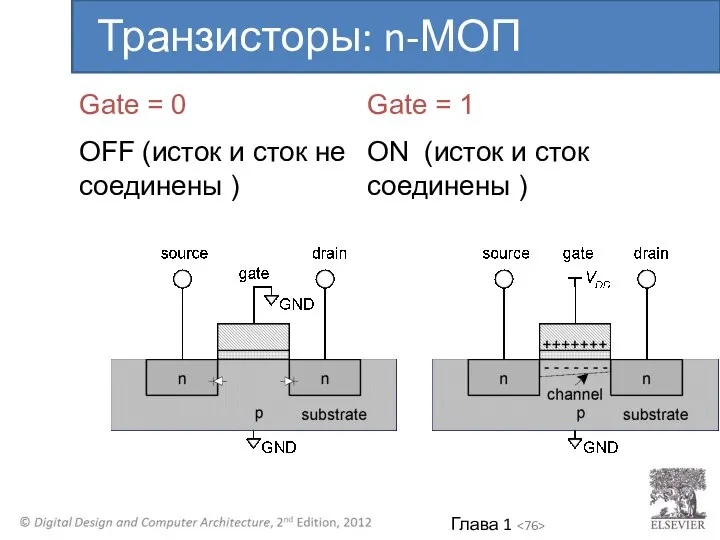
- 76. Gate = 0 OFF (исток и сток не соединены ) Gate = 1 ON (исток и
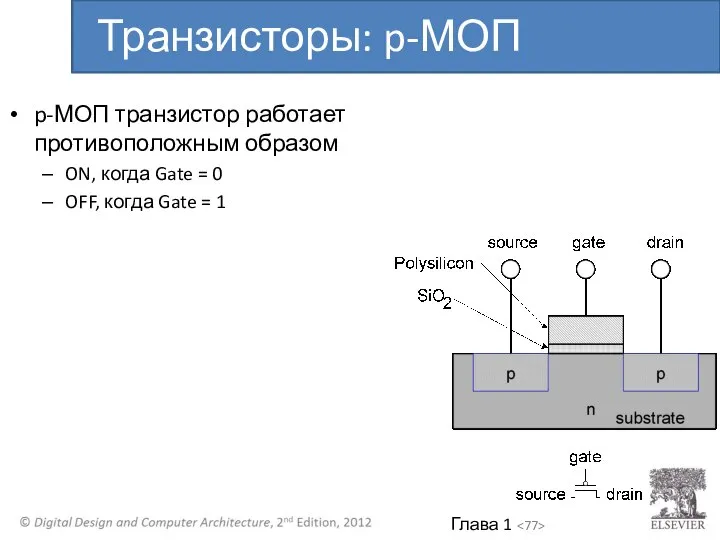
- 77. p-МОП транзистор работает противоположным образом ON, когда Gate = 0 OFF, когда Gate = 1 Транзисторы:
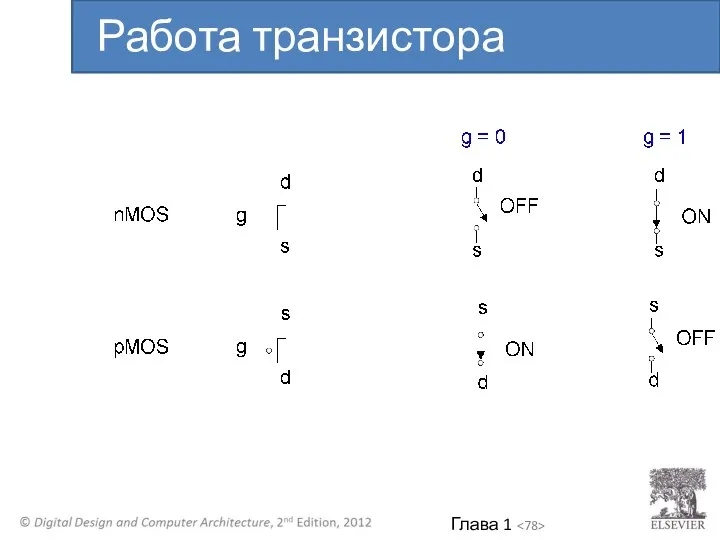
- 78. Работа транзистора
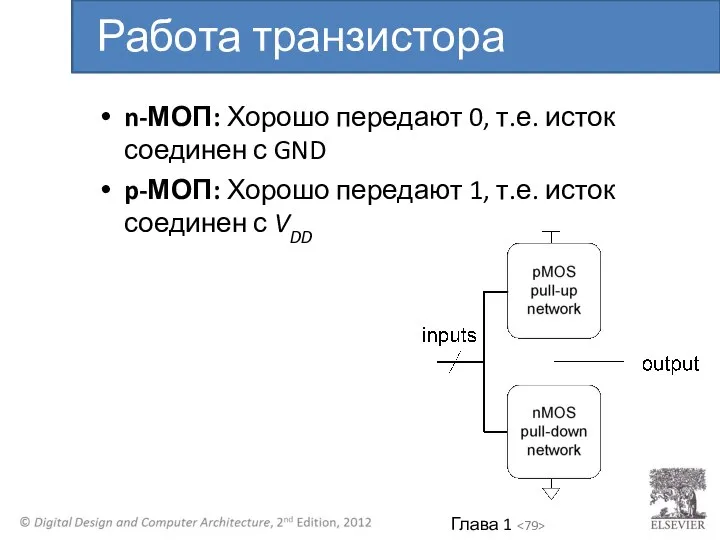
- 79. n-МОП: Хорошо передают 0, т.е. исток соединен с GND p-МОП: Хорошо передают 1, т.е. исток соединен
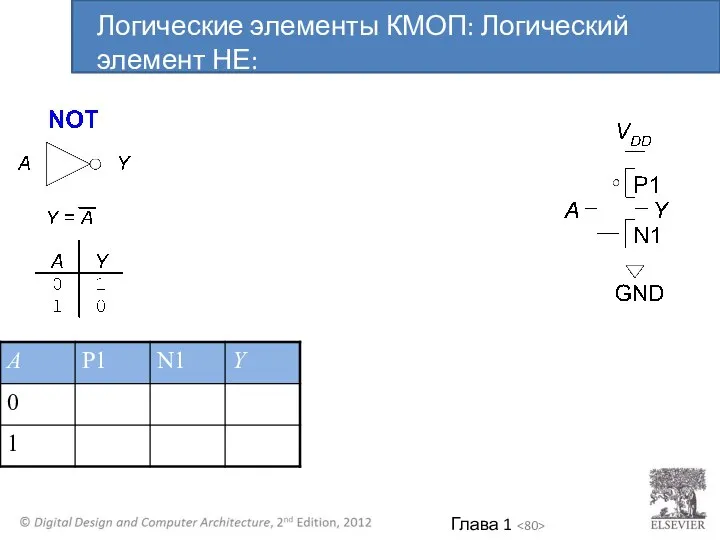
- 80. Логические элементы КМОП: Логический элемент НЕ:
- 81. Логические элементы КМОП: Логический элемент НЕ:
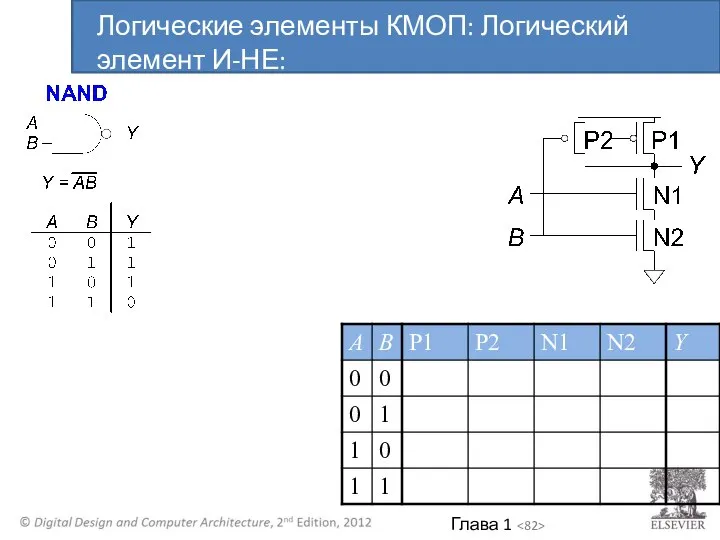
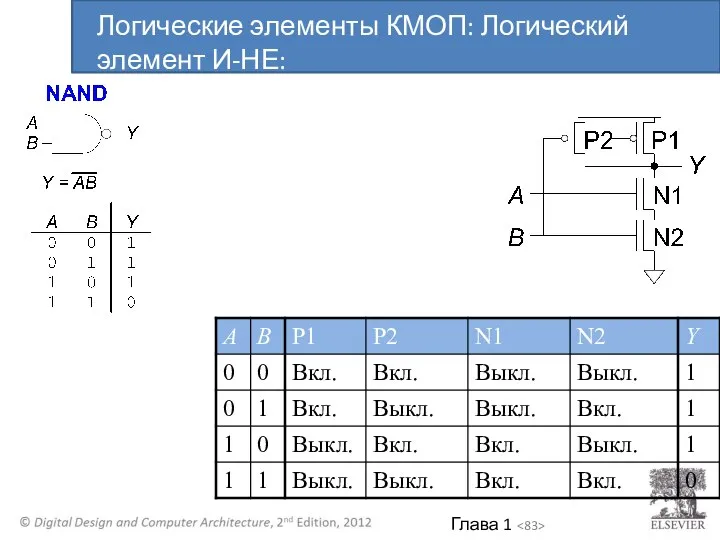
- 82. Логические элементы КМОП: Логический элемент И-НЕ:
- 83. Логические элементы КМОП: Логический элемент И-НЕ:
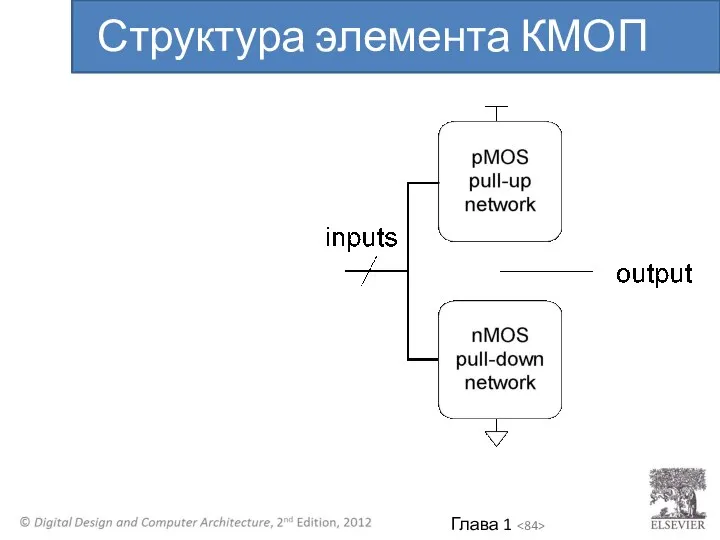
- 84. Структура элемента КМОП
- 85. Как построить элемент ИЛИ-НЕ? Логический элемент ИЛИ-НЕ
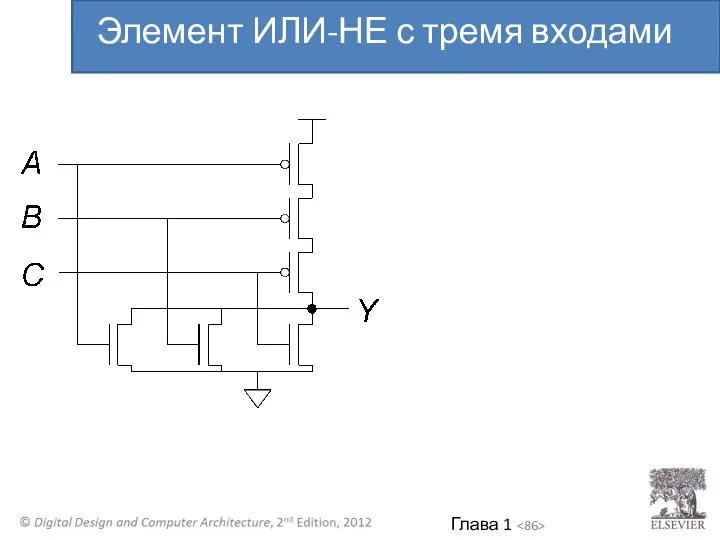
- 86. Элемент ИЛИ-НЕ с тремя входами
- 87. Как построить элемент И с двумя входами? Другие элементы КМОП
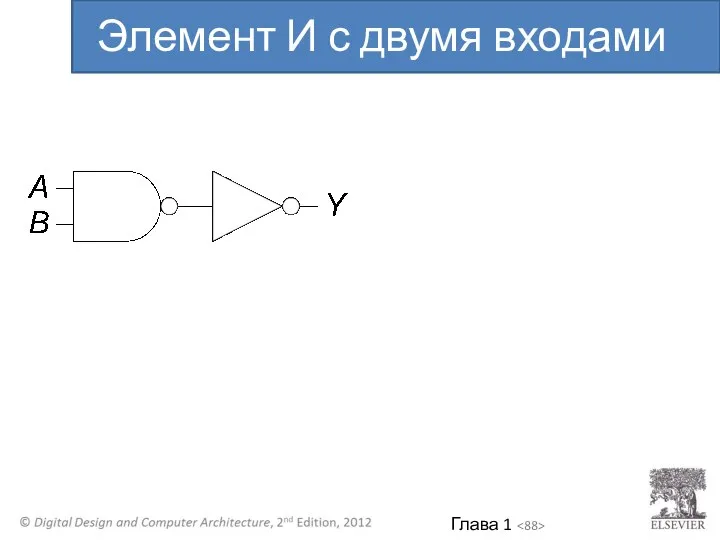
- 88. Элемент И с двумя входами
- 89. n-МОП плохо передают 1 p-МОП плохо передают 0 Передаточный логический элемент лучший выключатель хорошо передает и
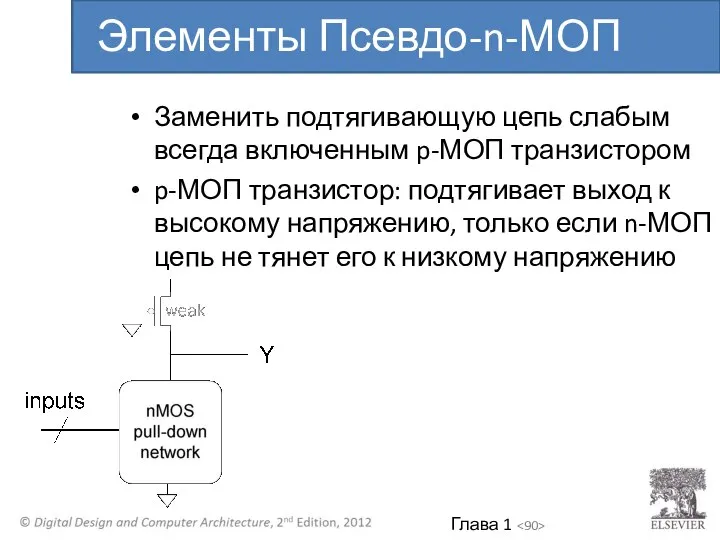
- 90. Заменить подтягивающую цепь слабым всегда включенным p-МОП транзистором p-МОП транзистор: подтягивает выход к высокому напряжению, только
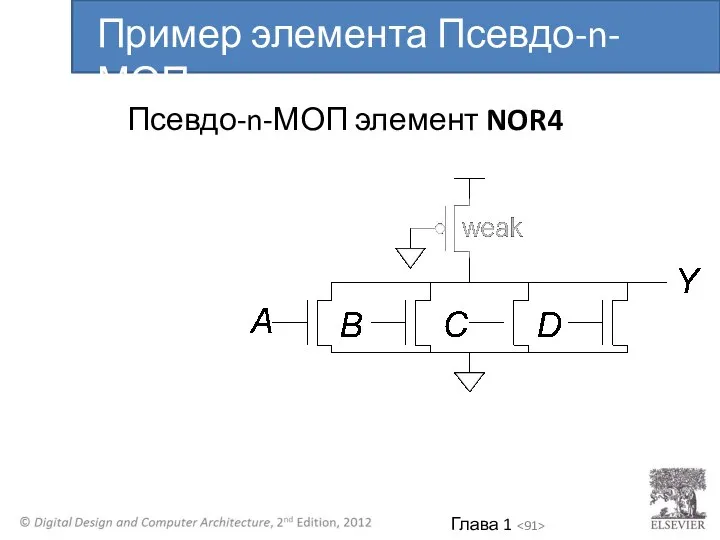
- 91. Псевдо-n-МОП элемент NOR4 Пример элемента Псевдо-n-МОП
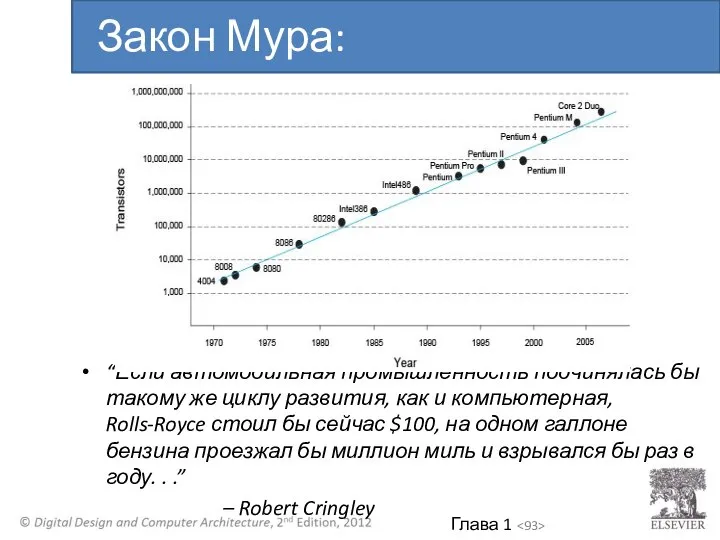
- 92. Со-основатель (вместе с Робертом Нойсом) Intel в 1968 году Закон Мура: количество транзисторов на микросхеме удваивается
- 93. “Если автомобильная промышленность подчинялась бы такому же циклу развития, как и компьютерная, Rolls-Royce стоил бы сейчас
- 94. Мощность = Потребление энергии в единицу времени Динамическая потребляемая мощность Статическая потребляемая мощность Энергопотребление
- 95. Мощность идет на зарядку емкостей заторов транзисторов Для зарядки конденсатора емкостью C до напряжения VDD необходима
- 96. Мощность, потребляемая, когда элементы не переключаются Обусловлена токами покоя (токами утечки), IDD Статическая потребляемая мощность: Pstatic
- 97. Оцените мощность, потребляемую беспроводным переносным компьютером VDD = 1.2 В C = 20 нФ f =
- 99. Скачать презентацию

















![N-разрядное десятичное число Сколько значений? 10N Диапазон? [0, 10N - 1] Пример:](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/944978/slide-20.jpg)


















































 История возникновения Всесоюзного физкультурного комплекса ГТО
История возникновения Всесоюзного физкультурного комплекса ГТО Железо – элемент побочной подгруппы
Железо – элемент побочной подгруппы Монтаж ОТИС
Монтаж ОТИС Русанова Наталья Леонидовна
Русанова Наталья Леонидовна Электро-диффузионные явления
Электро-диффузионные явления  Отдельностоящие плиты. Новинки 2011
Отдельностоящие плиты. Новинки 2011 Мир отношений. Отношения с самим собой, с миром и людьми
Мир отношений. Отношения с самим собой, с миром и людьми 50 наиболее востребованных на рынке труда, новых и перспективных профессий, требующих среднего профессионального образования
50 наиболее востребованных на рынке труда, новых и перспективных профессий, требующих среднего профессионального образования Текстиль
Текстиль Основные сюжеты и образы иконописи: иконы Праздников
Основные сюжеты и образы иконописи: иконы Праздников Публичный отчет директора гимназии №1за 2011-2012 учебный год
Публичный отчет директора гимназии №1за 2011-2012 учебный год Виды скульптуры по назначению
Виды скульптуры по назначению История России 10 класс
История России 10 класс Предложение фирмы «Проектика» по производству и поставке торгового оборудования Рязань 2012 Россия, 390029, г.Рязань, ул.Чкалова, 68А Тел
Предложение фирмы «Проектика» по производству и поставке торгового оборудования Рязань 2012 Россия, 390029, г.Рязань, ул.Чкалова, 68А Тел Презентация на тему Сохранение психологического и физического здоровья педагога
Презентация на тему Сохранение психологического и физического здоровья педагога  Специализированные учреждения ООН в современной системе международных отношений
Специализированные учреждения ООН в современной системе международных отношений Типы организационных теорий и их принципы. (Тема 2)
Типы организационных теорий и их принципы. (Тема 2) Отряды птиц
Отряды птиц Социальные игры Презентация для рекламодателей. - презентация
Социальные игры Презентация для рекламодателей. - презентация ТиТСП 3-1
ТиТСП 3-1 Wearable продукт
Wearable продукт Сигары
Сигары «1С:Предприятие 8. Оперативная печать»
«1С:Предприятие 8. Оперативная печать» Alles rund um die Geschichte und Freizeitorte Passau
Alles rund um die Geschichte und Freizeitorte Passau ОЦЕНКА ДОСТИЖЕНИЯ РЕЗУЛЬТАТОВ ОБУЧЕНИЯ ЧЕРЕЗ ИЗМЕРЕНИЕ ИЗМЕНЕНИЙ В ОБУЧАЮЩЕМСЯ Е. Б. Бухарова Директор Института экономики, уп
ОЦЕНКА ДОСТИЖЕНИЯ РЕЗУЛЬТАТОВ ОБУЧЕНИЯ ЧЕРЕЗ ИЗМЕРЕНИЕ ИЗМЕНЕНИЙ В ОБУЧАЮЩЕМСЯ Е. Б. Бухарова Директор Института экономики, уп Қазіргі замандағы әлемдік діндер
Қазіргі замандағы әлемдік діндер Грантрайдинг: упаковка проекта
Грантрайдинг: упаковка проекта Презентация на тему Борьба организма с инфекцией Иммунитет
Презентация на тему Борьба организма с инфекцией Иммунитет