Многогранники. Пирамиды

Основные вопросы темы
1.Определение
2.Элементы
3.Виды(подвиды)
4.Общие сведения

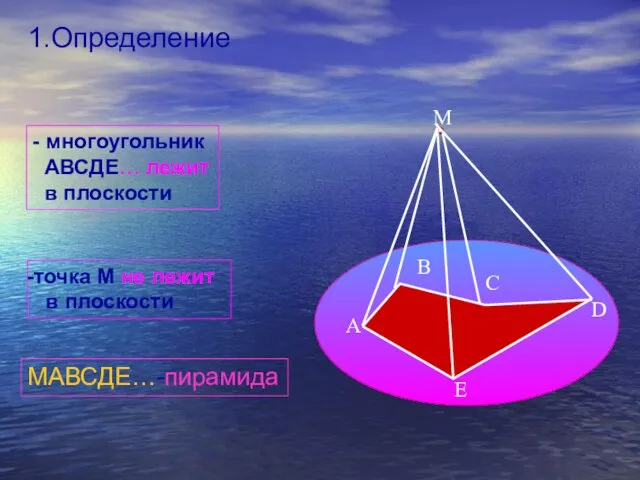
1.Определение
- многоугольник
АВСДЕ… лежит
в плоскости
точка М не лежит
в плоскости
МАВСДЕ…-пирамида

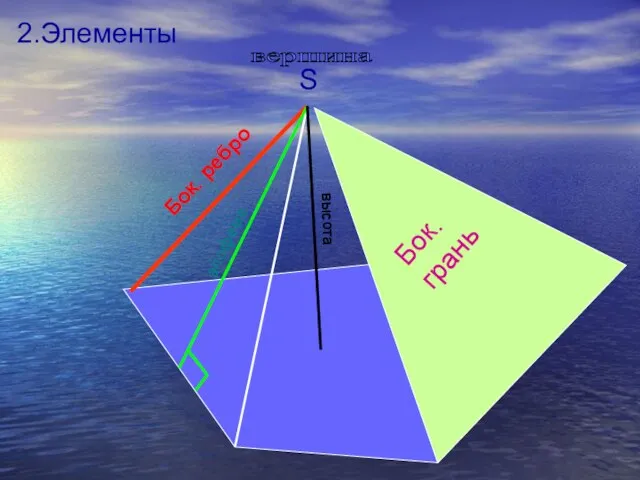
S
вершина
высота
апофема
Бок.
грань
2.Элементы
Бок. ребро

Площадь поверхности
Sбок = S1 + S2 + … + Sn
Сумма площадей боковых граней
Sпол = Sбок + Sосн

Обычные.
Название пирамиды определяется
по названию многоугольника,
лежащего в основании пирамиды.
Например:

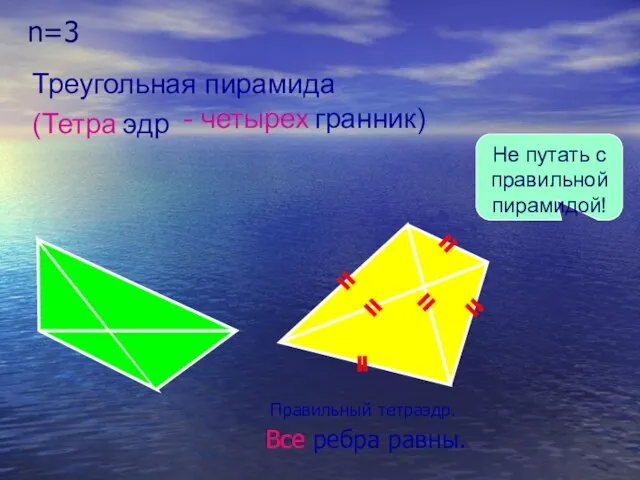
n=3
Правильный тетраэдр.
Все ребра равны.
Не путать с правильной пирамидой!
Треугольная пирамида

n=4
Четырехугольная пирамида
Пирамида Хеопса
в Гизе (долина царей).

n=6
Шестиугольная пирамида

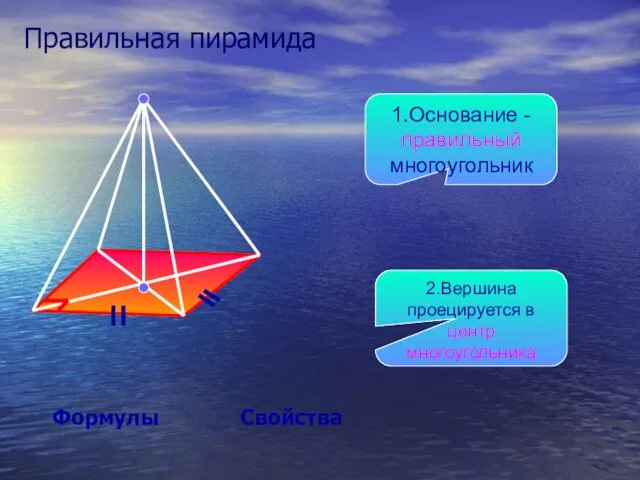
Правильная пирамида
Свойства
Формулы
1.Основание -
правильный многоугольник
2.Вершина проецируется в центр многоугольника

Свойства правильной пирамиды
Основание - правильный многоугольник.
2.Проекция вершины – центр вписанной и
описанной окружностей.
3.Все боковые ребра равны.
4.Все боковые ребра равнонаклонены к основанию.
5.Все двугранные углы равны.
6.Все апофемы равны.
7.Все плоские углы при вершине равны.

Формулы
Sбок=
S1+
S2+
…+
Sn=
=0,5 a1 * ha + 0,5 a2 * ha +…+ 0,5 an * ha=
=0,5ha * (a1 + a2 + … + an)=
Периметр основания
= 0,5 ha * P осн.
Sбок =0,5 Росн.* ha

1
2
1
2

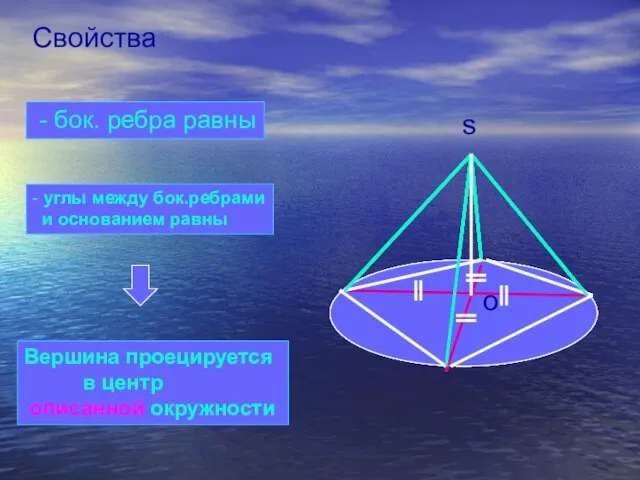
o
Свойства
- бок. ребра равны
- углы между бок.ребрами
и основанием равны
Вершина проецируется в центр
описанной окружности

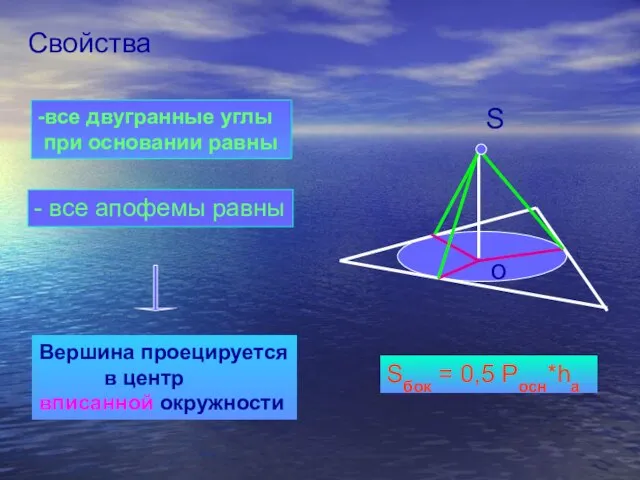
Свойства
-все двугранные углы
при основании равны
- все апофемы равны
Вершина проецируется
в центр
вписанной окружности
S
o
Sбок = 0,5 Росн*ha

4.Общие сведения
История
Современность
Биологическое
воздействие

Исторические сведения
Долина царей
«Красная» пирамида в Дашуре
Ступенчатая пирамида Джосера
Пирамида естественного
происхождения

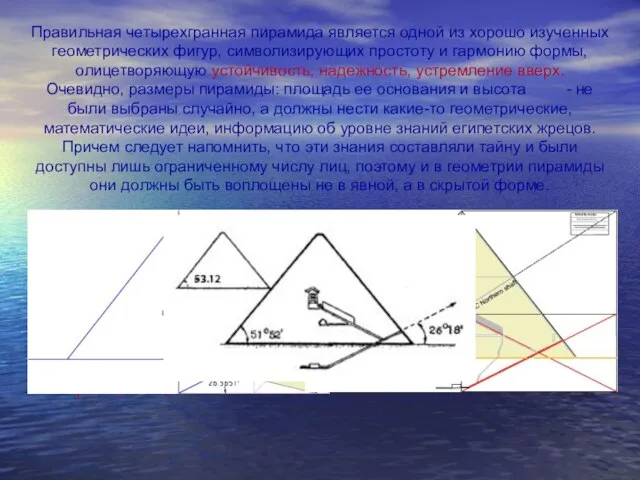
Геометрия Великой пирамиды
Простые геометрические соотношения между элементами внутреннего строения пирамиды Хеопса позволяют получить представление о первоначальном замысле древних архитекторов.

Вот что на сегодняшний день известно о единственном из сохранившихся семи чудес света - пирамиде Хеопса: построена примерно 4500 лет назад во времена IV династии фараонов Древнего Египетского Царства, высота - 146.5 м (сейчас примерно 8 м верхушки отсутствует, как и внешняя облицовка), длина стороны - 230.5 м . Пирамида выложена из 2.5 миллионов блоков песчаника весом от 0.5 до 2 тонн .

Правильная четырехгранная пирамида является одной из хорошо изученных геометрических фигур, символизирующих простоту и гармонию формы, олицетворяющую устойчивость, надежность, устремление вверх.
Очевидно, размеры пирамиды: площадь ее основания и высота - не были выбраны случайно, а должны нести какие-то геометрические, математические идеи, информацию об уровне знаний египетских жрецов. Причем следует напомнить, что эти знания составляли тайну и были доступны лишь ограниченному числу лиц, поэтому и в геометрии пирамиды они должны быть воплощены не в явной, а в скрытой форме.
Гениальные создатели пирамиды Хеопса стремились поразить далеких потомков глубиной своих знаний, и они достигли этого. Следует лишь удивляться высокому знанию и искусству древних математиков и архитекторов Египта, которые смогли воплотить в пирамиде две иррациональные (т.е. неизмеримые) величины – π и Ф со столь поразительной точностью, оперируя исходными отношениями целых чисел – стороной основания и высотой
пирамиды, выраженных в локтях.

«Большой Лувр» после
реставрации в 1981 г.
Связь между новыми залами
и двором осуществляется с помощью пирамиды из прозрачного стекла необычайно легкой конструкции.
Автором этого новаторского
проекта был американский
архитектор китайского
происхождения Ео Минг Пей.

Французский ученый Жак Бержье, изучавший влияние различных пространственных форм на биологические вещества, соорудил картонную модель Пирамиды и поместил туда бычью кровь. Через некоторое время она разделилась на две субстанции - светлую и темную. Другие ученые удостоверились, что в модели Пирамиды долго сохраняются скоропортящиеся продукты. Маятник, подвешенный над вершиной модели, отклоняется в сторону или медленно вращается вокруг вершины. Странно ведут себя и растения. Сначала они тяготеют к востоку, потом описывают полукруг, двигаясь с юга на запад. Чешский изобретатель Карел Дрбал в 1959 году приспособил подобную модель для самозатачивания бритвенных лезвий, и получил патент на это необычное изобретение.! Считается, что пирамидальная форма фокусирует космическую энергию...
Биологическое воздействие

Задания
1.Сколько граней, вершин, ребер у n-угольной пирамиды?
2.Какое наименьшее число граней, вершин, ребер может иметь пирамида?
3.Высота пирамиды равна 3см. Чему равно расстояние от вершины пирамиды до плоскости основания?
4.Какие многоугольники могут быть сечением 4-х угольной пирамиды?
5.Боковые ребра треугольной пирамиды равны 7см, 12см и 5см. Одно из них перпендикулярно к плоскости основания. Чему равна высота пирамиды?
6.Одно из боковых ребер пирамиды равно 12см, а ее высота – 6см. Найдите угол между этим ребром и плоскостью основания пирамиды.
7.Все плоские углы при вершине треугольной пирамиды прямые, а выходящие из нее ребра равны 2м, 4м и 6м.Найдите площадь боковой поверхности пирамиды.
8.Основание пирамиды – правильный 6-ти угольник. Найдите величину угла, образованного двумя гранями пирамиды, если их общее ребро перпендикулярно к плоскости основания.
9.Основание пирамиды – 4-х угольник все стороны которого равны. Высота пирамиды проходит через точку пересечения диагоналей основания. Является ли данная пирамида правильной?
10.Сторона основания правильной 6-ти угольной пирамиды равна 1м, а боковое ребро – 2м. Найдите: а) высоту пирамиды б) угол между боковым ребром и плоскостью основания пирамиды.
11.Сторона основания правильной 4-х угольной пирамиды равна 6м, а боковое ребро – 5м. Найдите: а) апофему б) площадь боковой поверхности пирамиды.