Содержание
- 2. «Параллельный мир - нечто, состоящее из слов и линий» Помню снов тоску. Тогда перед зеркалом стоял
- 3. Две плоскости называются параллельными, если они не пересекаются. Плоскости Пересекаются Параллельны β α α || β
- 4. Параллельные плоскости в природе Если стоять спиной к водопаду, скалы образуют геометрически правильные параллельные плоскости
- 5. Параллельные плоскости в технике Параллельные плоскости «летают»
- 6. Параллельные плоскости в быту В своей сущности и основе геометрия –это пространственное воображение, пронизанное и организованное
- 7. Параллельные плоскости в искусстве Д.Грин «Мечты» Силуэты мальчика расположены в параллельных плоскостях
- 8. Невозможные структуры Жос Де Мей.(Jos de Mey) Жос де Мей (Jos de Mey) родился в 1928
- 9. Невозможные структуры Жос Де Мей.(Jos de Mey) Часто на картинах Жоса де Мея изображена сова. Эта
- 10. Невозможные фигуры возможны! Речной вокзал в Твери. Кстати, это место, где снимали несколько сцен фильма "Чучело".
- 11. Две плоскости называются параллельными, если они не пересекаются. Плоскости Пересекаются Параллельны β α α || β
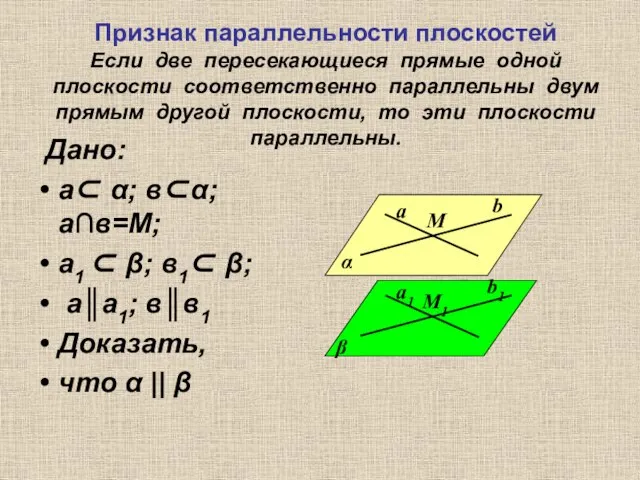
- 12. Признак параллельности плоскостей Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то
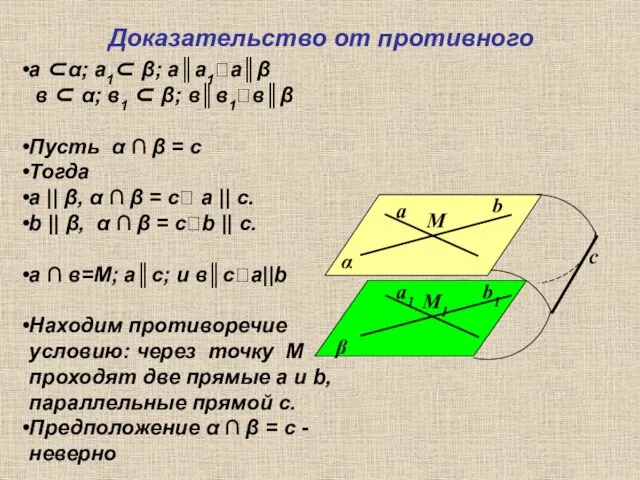
- 13. Доказательство от противного α β а b М b1 а1 М1 с а α; а1 β;
- 14. Какие теоремы мы использовали при доказательстве признака?
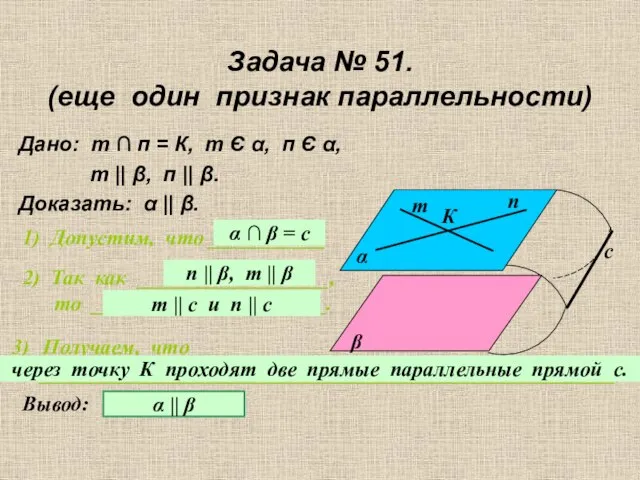
- 15. Задача № 51. (еще один признак параллельности) Дано: т ∩ п = К, т Є α,
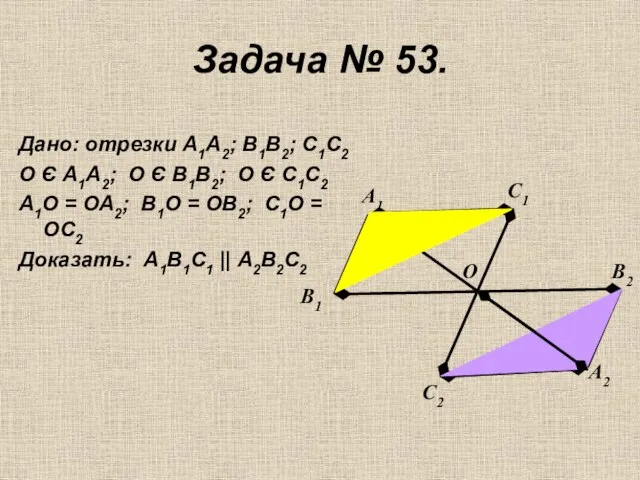
- 16. Задача № 53. Дано: отрезки А1А2; В1В2; С1С2 О Є А1А2; О Є В1В2; О Є
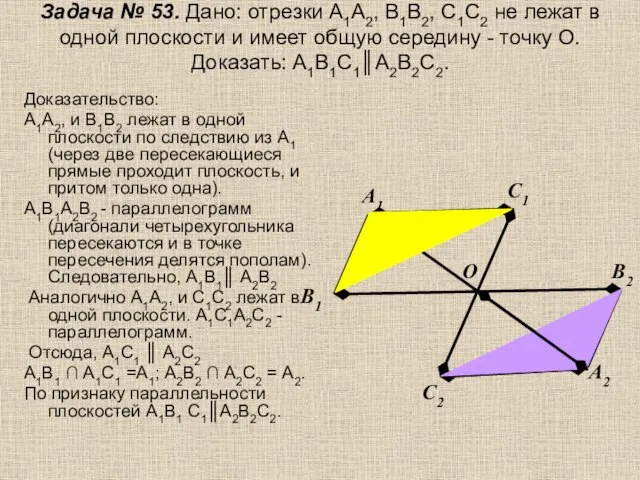
- 17. Задача № 53. Дано: отрезки А1А2, В1В2, С1С2 не лежат в одной плоскости и имеет общую
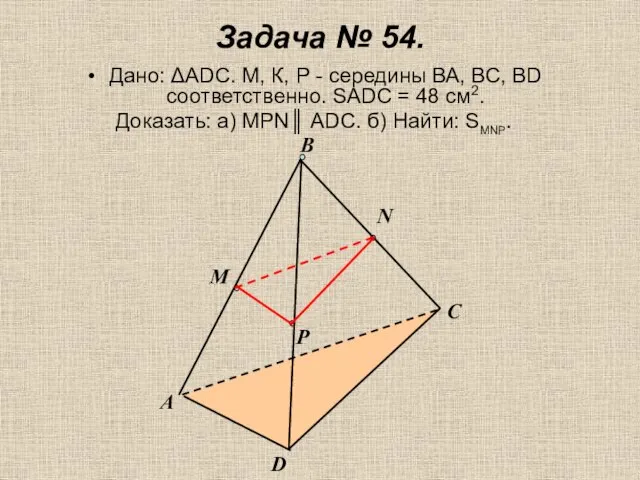
- 18. Задача № 54. Дано: ΔАDС. М, К, Р - середины ВА, ВС, ВD соответственно. SADC =
- 19. Отвечаем на вопросы Могут ли прямая и плоскость не иметь общих точек? Верно ли, что если
- 20. Проверяем свою работу Могут ли прямая и плоскость не иметь общих точек? Да Верно ли, что
- 22. Скачать презентацию











 Животные. Брачные обряды
Животные. Брачные обряды Клинический случай. Корь у привитого ребенка 1,6 лет с неустановленным контактом
Клинический случай. Корь у привитого ребенка 1,6 лет с неустановленным контактом Обучение иностранным языкам в современной информационно- образовательной среде
Обучение иностранным языкам в современной информационно- образовательной среде 30 апреля – 5 мая 2012 года
30 апреля – 5 мая 2012 года Презентация на тему Япония 7 класс
Презентация на тему Япония 7 класс Требуются рабочие ООО РосПромПерсонал
Требуются рабочие ООО РосПромПерсонал Презентация на тему файлы и папки 6 класс презентация
Презентация на тему файлы и папки 6 класс презентация  Принцесса Рапунцель
Принцесса Рапунцель Презентация на тему Конституционные обязанности человека и гражданина
Презентация на тему Конституционные обязанности человека и гражданина Шумоанализация или Как шум влияет на здоровье и внимание школьника
Шумоанализация или Как шум влияет на здоровье и внимание школьника Главные типы почв России
Главные типы почв России СИСТЕМА МЕНЕДЖМЕНТА КАЧЕСТВА в СГТА
СИСТЕМА МЕНЕДЖМЕНТА КАЧЕСТВА в СГТА Политология. Лекция 3.1
Политология. Лекция 3.1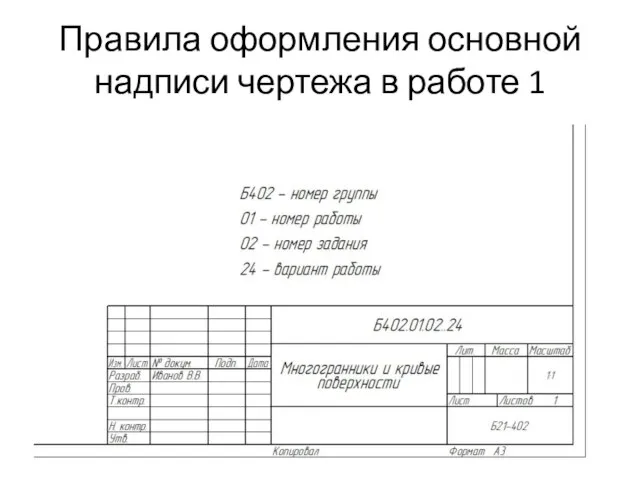 Правила оформления основной надписи чертежа в работе 1
Правила оформления основной надписи чертежа в работе 1 ООО «ЭкоЛайф 69»
ООО «ЭкоЛайф 69» Презентация на тему Информация и цивилизация
Презентация на тему Информация и цивилизация Étude deefine
Étude deefine Лекция 3 - Вывод уравнений узловых напряжений
Лекция 3 - Вывод уравнений узловых напряжений Система оценка качества образования в Забайкальском крае
Система оценка качества образования в Забайкальском крае Волшебный мир
Волшебный мир Внешняя политика СССР в 1930-е гг. и накануне Великой Отечественной войны
Внешняя политика СССР в 1930-е гг. и накануне Великой Отечественной войны Введение компетентностного подхода в современное образование
Введение компетентностного подхода в современное образование Ama Kids, рейтинг
Ama Kids, рейтинг Ресинхронизирующая терапия при ХСНMеханизмы, клиничексие аспекты, выбор пациента, имплантация
Ресинхронизирующая терапия при ХСНMеханизмы, клиничексие аспекты, выбор пациента, имплантация Исследовательская деятельность
Исследовательская деятельность OS definition
OS definition Физические явления
Физические явления Сценарнорежиссерские основы культурно-досуговых программ
Сценарнорежиссерские основы культурно-досуговых программ