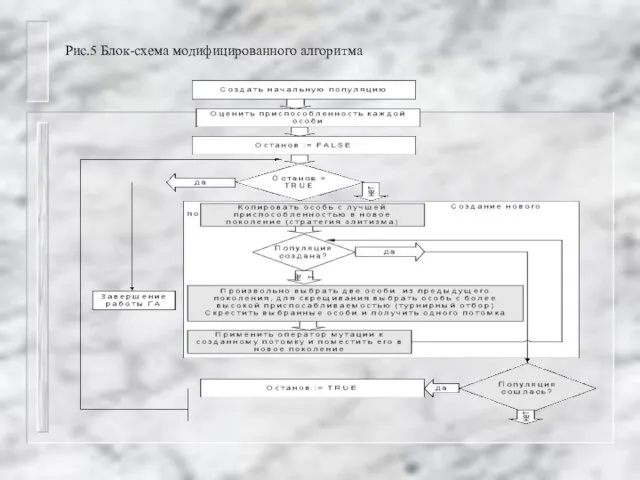
Слайд 13В качестве математической модели СКС будем использовать гиперсеть .
Одним из основных понятий

у нас будет фигурировать гиперсеть с иерархической вторичной сетью.
Формально гиперсеть можно определить шестёркой AS = (X, V, R, P, F,W)
Абстрактной гиперсетью AS назовём совокупность, включающую такие объекты:
X =(x1,..xn)- множество вершин;
V=(v1,..,vg)- множество ветвей;
R=(r1,..,rm)- множество рёбер;
P: V → 2x- отображение, сопостовляющее каждому элементу r∈R множество P(v) из X его вершин.Тем самым отображение Р определяет гиперграф PS=(X,V,P).
F: R → 2VPS – отображение, сопостовляющее каждому элементу r ∈R множество P(v) его ветвей. Причём семейство подмножеств ветвей 2VPS содержит такие подмножества, ветви которых состовляют связную часть гиперграфа FS=(V, R, F);
Для любого r ∈ R W: r → 2P(F(r))- отображение, сопостовляющее каждому элементу r∈R подмножество W(r) ∈P(F(r)) его вершин, где P(F(r)) – множество вершин в PS, инцидентных ветвям F(r) из V .Таким образом, отображение W определяет гиперграф WS=(X, R, W).
Абстрактная гиперсеть называется гиперсетью, если для любых v,r принадлежащих V, R | P(v) | = |W(r)| = 2. А для любоых r из R множество F(r) входящее в V составляет маршрут в графе PS=(X,V).
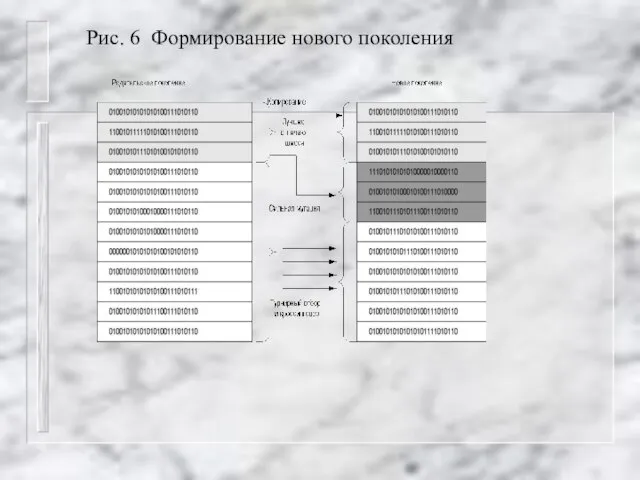
Таким образом, первичная PS и вторичная сети WS гиперсети S являются графами, а F отображает рёбра WS =(X,R) в маршруты графа PS=(X,V).
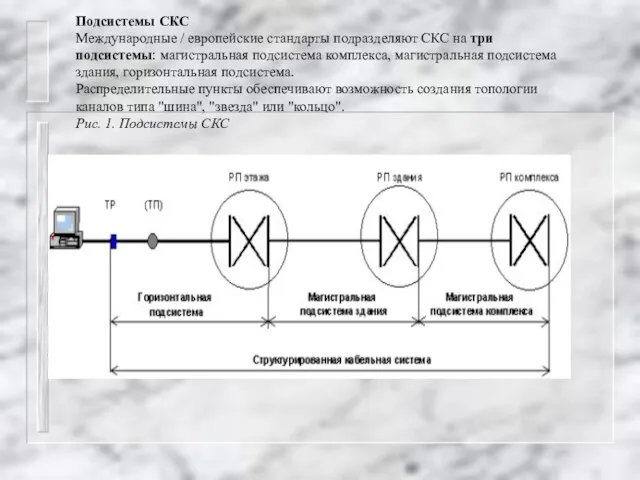
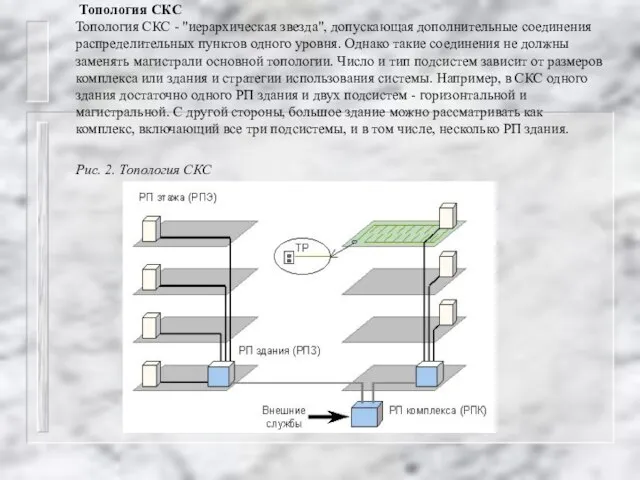
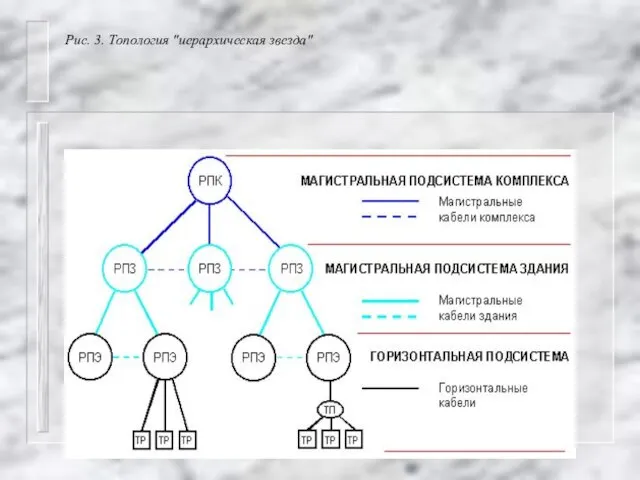
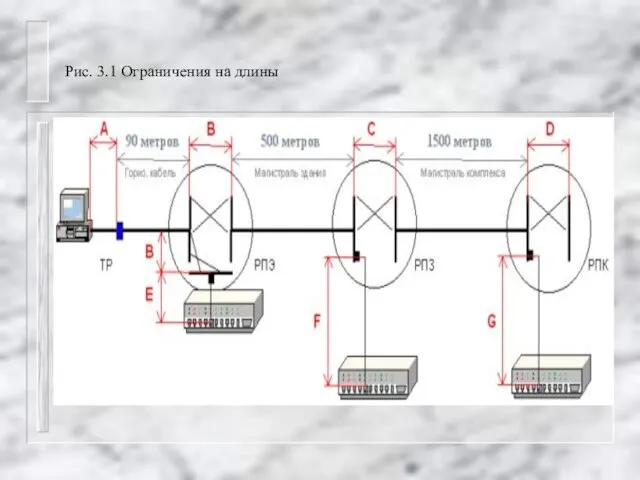
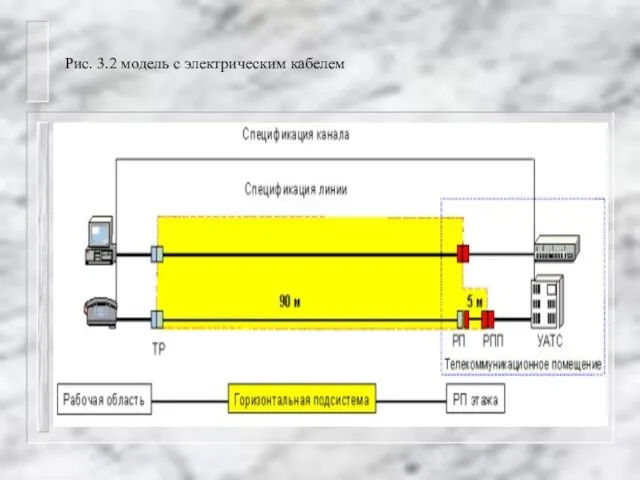
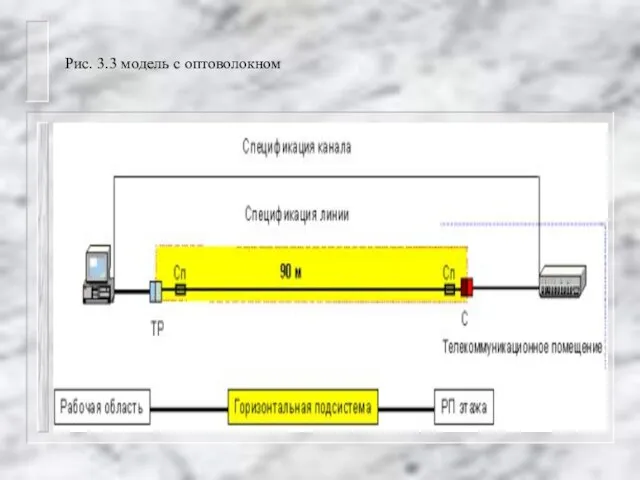
Рассмотрим теперь структуру СКС с учётом разделения её на подсистемы. Зададим структурированную кабельную систему гиперсетью N=(X,V,A,B,C), где:
X=(x1,..xn)- множество вершин
V=(v,..,v) – множество ветвей
A=(a,..,a) – множество рёбер внешней магистрали
B=(b,..,b) – множество рёбер внутренней магистрали
C=(c,..,c) – множество рёбер горизонтальной магистрали
R= A+B+C .











 Номенклатура алканов разветвлённого строения
Номенклатура алканов разветвлённого строения Симметрия и движение (9 класс)
Симметрия и движение (9 класс) Творческий проект
Творческий проект Составное глагольное сказуемое
Составное глагольное сказуемое Бартоломео Франческо Растрелли
Бартоломео Франческо Растрелли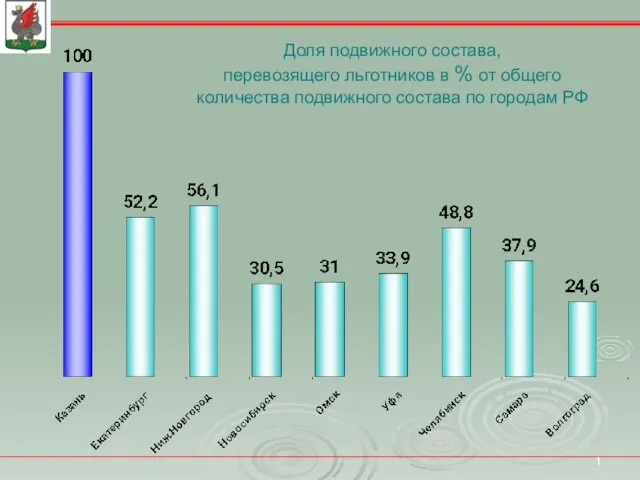 Доля подвижного состава, перевозящего льготников в % от общего количества подвижного состава по городам РФ
Доля подвижного состава, перевозящего льготников в % от общего количества подвижного состава по городам РФ О компании
О компании Конституция - основной закон государства
Конституция - основной закон государства Интересное проектирование – делимся опытом! Траверса для контейнера САО тип I и тип II
Интересное проектирование – делимся опытом! Траверса для контейнера САО тип I и тип II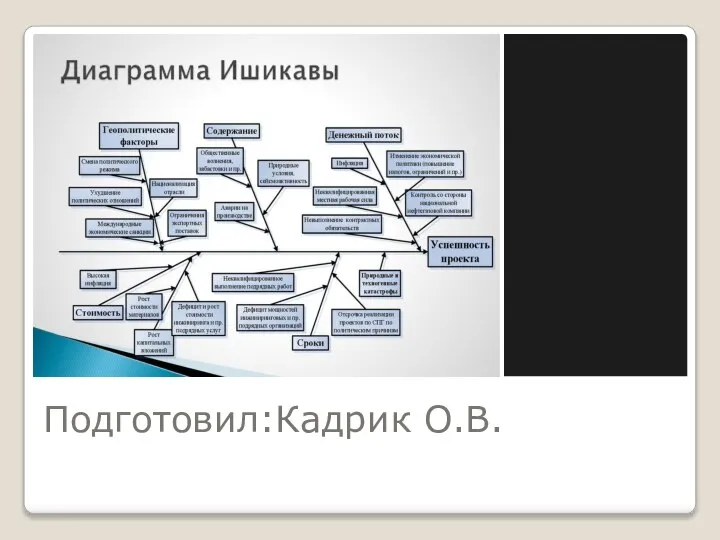 Диаграмма Ишикава. Алгоритм формирования диаграммы
Диаграмма Ишикава. Алгоритм формирования диаграммы Оплата труда гражданских служащих: новые подходы
Оплата труда гражданских служащих: новые подходы Добро пожаловать!!
Добро пожаловать!! Опыт работы администрации городского округа «Город «Хабаровск» в сфере профилактики социального сиротства, безнадзорности нес
Опыт работы администрации городского округа «Город «Хабаровск» в сфере профилактики социального сиротства, безнадзорности нес Скажи мне, как тебя зовут...
Скажи мне, как тебя зовут... Тема проекта:“Диета: за и против.”
Тема проекта:“Диета: за и против.” Культурное растение: «Чай»
Культурное растение: «Чай» СОХРАНИМ ОСТРОВА ДИКОЙ ПРИРОДЫ В ОКЕАНЕ ЦИВИЛИЗАЦИИ
СОХРАНИМ ОСТРОВА ДИКОЙ ПРИРОДЫ В ОКЕАНЕ ЦИВИЛИЗАЦИИ Ребята, давайте жить дружно!
Ребята, давайте жить дружно! Учет движения товаров. Приходные и расходные товарные операции
Учет движения товаров. Приходные и расходные товарные операции Лабораторный практикум Excel
Лабораторный практикум Excel Школьный этикет
Школьный этикет Алфавит в стихах
Алфавит в стихах Современное выставочное пространство Санкт-Петербурга
Современное выставочное пространство Санкт-Петербурга Драгоценные и поделочные камни - соединения кремния
Драгоценные и поделочные камни - соединения кремния Формула сайта:Успешный интернет-магазин от А до Я
Формула сайта:Успешный интернет-магазин от А до Я Factors Driving Industry Change
Factors Driving Industry Change  «Создание ароматических композиций из эфирных масел в условиях малой химической лаборатории»
«Создание ароматических композиций из эфирных масел в условиях малой химической лаборатории» Презентация на тему Как вести себя в конфликтной ситуации
Презентация на тему Как вести себя в конфликтной ситуации