Моделирование поляризационной неустойчивости в эрбиевых волоконных лазерах

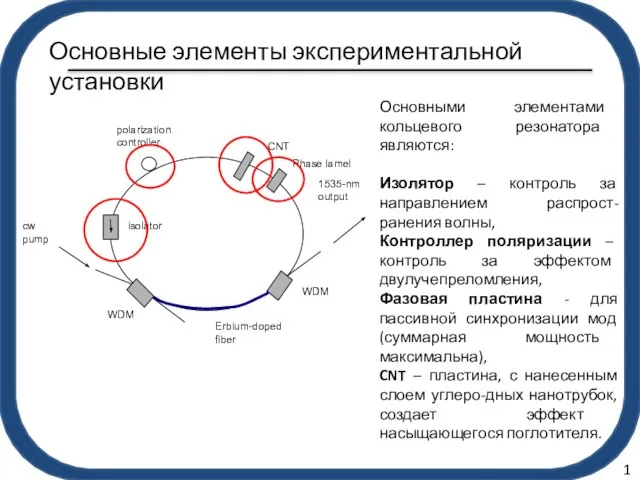
Основные элементы экспериментальной установки
Основными элементами кольцевого резонатора являются:
Изолятор – контроль за направлением распрост-ранения волны,
Контроллер поляризации – контроль за эффектом двулучепреломления,
Фазовая пластина - для пассивной синхронизации мод (суммарная мощность максимальна),
CNT – пластина, с нанесенным слоем углеро-дных нанотрубок, создает эффект насыщающегося поглотителя.
1

Математическая модель
В основе математической модели лежат уравнения Максвелла, нормированные на время обхода волны резонатора.
2
*
Eammanuel Desurvire «Erbium Doped Fiber Amplifiers»
S.V. Sergeev «Spontaneous light-polarization symmetry breaking for an anisotropic ring-cavity die laser» », Physical Rewiew a, vol.59, 1999.
H. Zeghlache, A. Boulnois «Polarization instability in lasers. I. Model and steady states of noedymium-doped fiber lasers», Physical Rewiew A, vol.52, 1995;

Математическая модель.
Допущения.
Переход от модели Nd – лазера или лазера на красителях к модели легированного Er лазера возможен благодаря:
Аналогичной 4 – х уровневой системы возбужденных состояний атома Er;
Записи уравнений поля, учитывающей только общие эффекты (такие эффекты как, например, броуновское движение молекул в красителе, вводятся в систему позже в виде дополнительных членов);
Записи уравнений для эволюции поля, позволяющей не учитывать специфичность резонатора на красителях (пространственное распределение компонент поля).
3

Математическая модель.
Уравнения поляризационной динамики*.
4
*получена Сергеем Сергеевым

Эффекты поляризационной динамики
Спонтанное нарушение поляризации
Поляризационный выжиг дыр
5

Используемые параметры:
α1 = 800/ln(10) - нормированное усиление для Er
α2 = 0.136 - поглощение сигнала в нанотрубках
α3 = 0.001 - Psat/PEr
α4 = 50/ln(10) - нормированные потери в резонаторе
β = 5/3 - (σem - σabs)/σabs
(maep)2 = 0.5 - циркулярно поляризованная накачка
Ip = 50 - мощность накачки
ε = 10-4 - oтношение времени обхода резонатора
к времени жизни в первом возбужденном
состоянии для Er
δ = 10-4 - коэффициент спонтанной эмиссии
ψ1= π/2, ψ3= π/4, ψ2 =0 - углы фазовых пластин
6

Параметры Стокса. Сфера Пункаре.
Сфера Пуанкаре:
Параметры Стокса:
7
А.П. Войтович «Лазеры с анизотропными резонаторами», Наука и техника, 1988

Численная Схема.
Метод Рунге-Кутты для жестких систем*.
Для нелинейной системы вида y’ = f(x, y):
8
* Е.А. Новиков «Явные методы для жестких систем», «Наука», Сибирское предприятие РАН, 1997

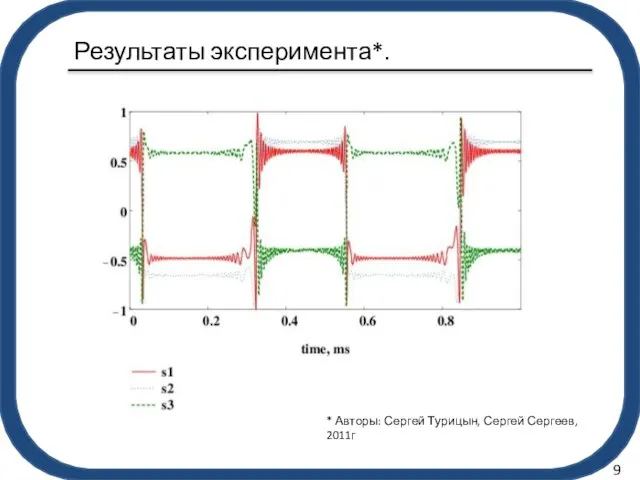
Результаты эксперимента*.
9
* Авторы: Сергей Турицын, Сергей Сергеев, 2011г

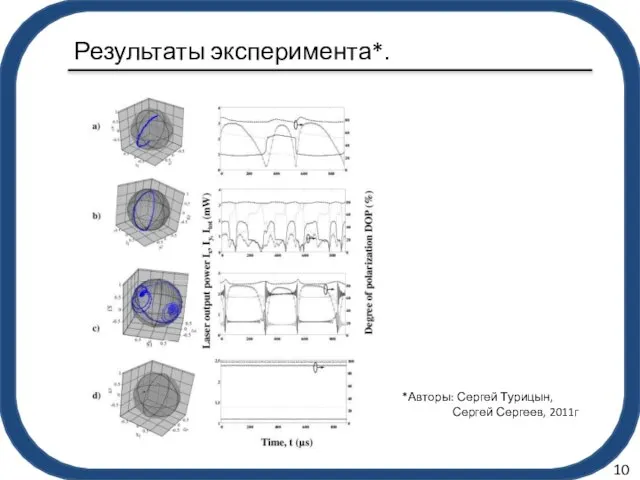
Результаты эксперимента*.
10
*Авторы: Сергей Турицын,
Сергей Сергеев, 2011г

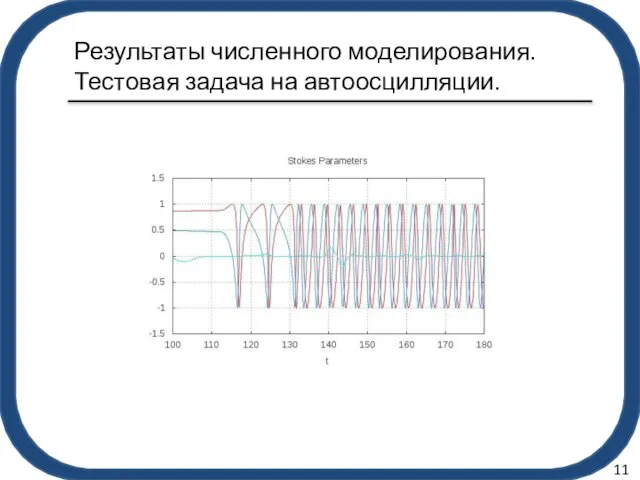
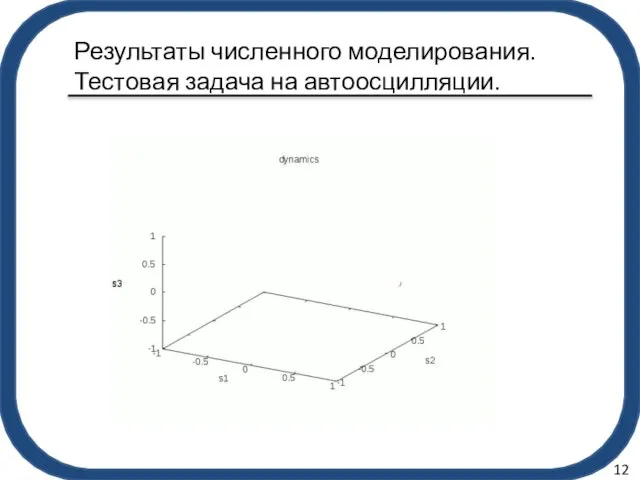
auto
Результаты численного моделирования.
Тестовая задача на автоосцилляции.
11

Результаты численного моделирования.
Тестовая задача на автоосцилляции.
12

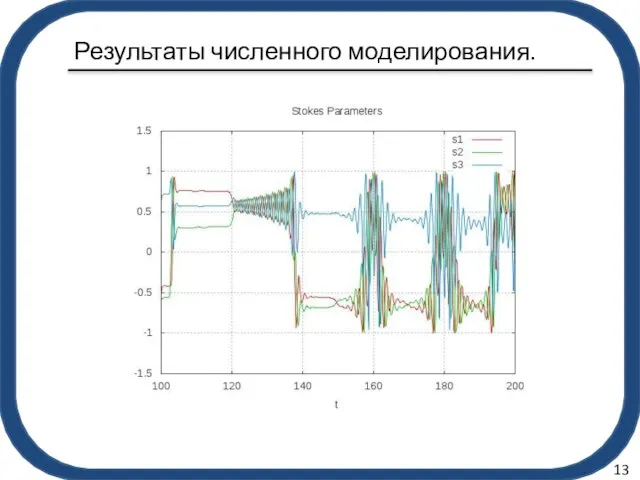
Результаты численного моделирования.
13

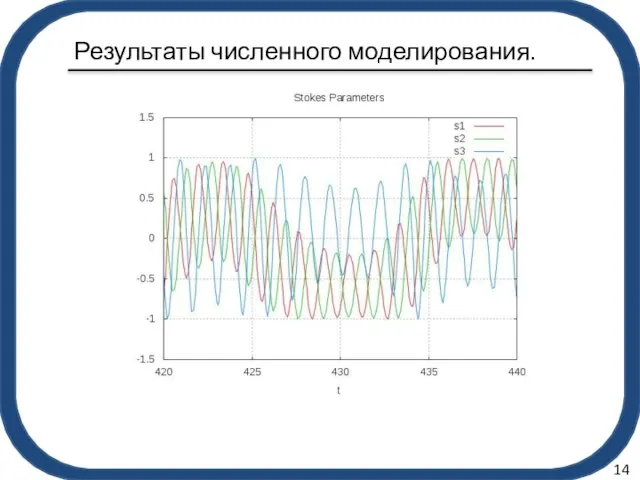
Результаты численного моделирования.
14

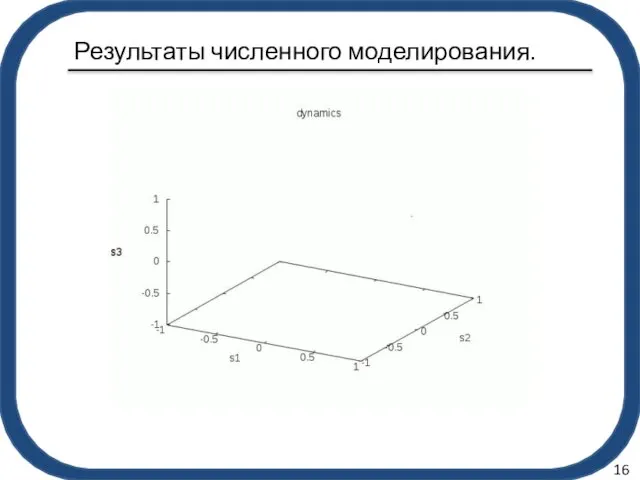
Результаты численного моделирования.
15

Результаты численного моделирования.
16