Моделирование процесса потребления

Моделирование процессов потребления
7. Оптимизационная модель задачи потребительского выбора.
Задача потребительского выбора имеет вид:
U(X) =>max (13.1)
(PX) ≤ K (13.2)
Xi ≥0
где: X={x1,x2,…,xn} – вектор набора товаров;
хi – количество товара вида i;
P={p1,p2,…,pn} – вектор цен на товары;
К – доход потребителя.

Моделирование процессов потребления
7. Оптимизационная модель задачи потребительского выбора.
Задача (13.1)-(13.2) может быть решена методом неопределенных множителей Лагранжа.
L(X,λ,μ)= U(X) +λ(K-(PX) +μX
где λ и μ множители Лагранжа.
Предполагая, что множество X не содержит товаров, которые не нужны потребителю, т.е. в нем все xi >0, необходимые условия экстремума функции Лагранжа примут вид:
∂U/∂x – λP = 0 (13.4)
λ(K- (PX)) = 0 (13.5)
K-(PX) ≥ 0 (13.6)
λ > 0 (13.7)
Эта система имеет решение относительно (n+1) переменной X и λ. Все производные, компоненты вектора X и λ вычисляются в точке оптимума X* и λ*.

Моделирование процессов потребления
7. Оптимизационная модель задачи потребительского выбора.
Из уравнения (13.4) для пары (X*, λ*) получим:
Вывод: в условиях оптимального выбора отношение предельной полезности товаров к цене постоянно для всех товаров.
Определение. Множитель Лагранжа λ* интерпретируется как предельная полезность одной денежной единицы или как предельная полезность денег.
Поэтому равенство (13.8) означает, что, если предельная полезность денег становится постоянной для каждого товара, тогда потребитель получает максимум полезности.
Из равенства (13.8) также следует, что:
Цены определяются исходя из предельных полезностей товаров и денег.
(13.8)

Моделирование процессов потребления
7. Оптимизационная модель задачи потребительского выбора.
Т.к. λ*>0 (следует из (13.4), то из (13.5) получаем, что:
К – (Р,Х*) = 0. Это означает, что точка максимума Х* задачи (13.1)-(13.2) лежит на бюджетной линии и является точкой касания бюджетной линии и кривой безразличия.
Предельная норма замещения товаров в оптимальном состоянии оценивается соотношением цен:
γji =(∂U/∂xi)/(∂U/∂xj) = Pi/Pj
Исходя из этих соотношений можно графически анализировать следующие задачи:
1. как изменится спрос на товары при изменении цен и неизменном доходе?
2. как изменится потребление при изменении цен и постоянной полезности (эффект замещения)
3. как изменится потребление при изменении дохода.

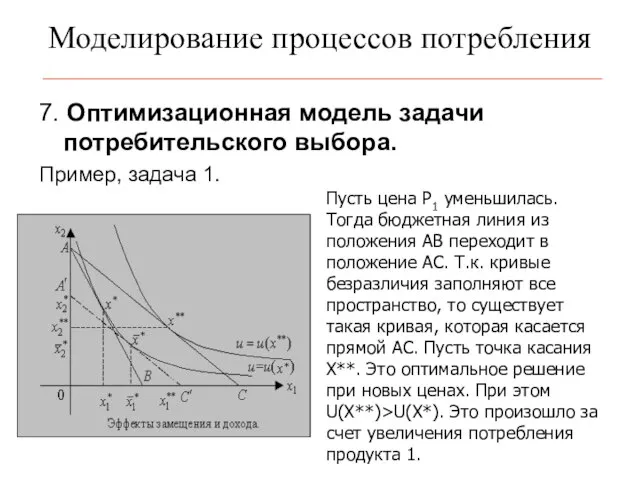
Моделирование процессов потребления
7. Оптимизационная модель задачи потребительского выбора.
Пример, задача 1.
Пусть цена Р1 уменьшилась. Тогда бюджетная линия из положения АВ переходит в положение АС. Т.к. кривые безразличия заполняют все пространство, то существует такая кривая, которая касается прямой АС. Пусть точка касания X**. Это оптимальное решение при новых ценах. При этом U(X**)>U(X*). Это произошло за счет увеличения потребления продукта 1.

Моделирование процессов потребления
8. Функция спроса потребителя.
Определение. Оптимальное решение задачи (13.1)-(13.2) называется функцией спроса потребителя.
Говорят так же, что спрос есть платежеспособная потребность.
Платежеспособность предполагает соответствие цен и дохода.
Поэтому общее решение задачи потребления является функцией цен и дохода.
В общем случае спрос D(P,K)-это совокупность правил, с помощью которых потребитель определяет свой спрос.
Если функция полезности строго вогнута, то функция спроса D(P,K) однозначна.
Доход потребителя К зависит от цен на товары, т.е К(Р), поэтому функцию спроса можно определить как D=D(P,K(P)).
При увеличении цен на товары, вообще говоря, доход потребителя должен быть компенсирован.
Это требование формализуется как свойство однородности первой степени функции дохода: K(αP) = αK(P).

Моделирование процессов потребления
8. Функция спроса потребителя.
Ясно, что, если повышение цен пропорциональным образом компенсируется повышением дохода, то спрос должен оставаться на прежнем уровне, т.е.
D(αP,K(αP))=D(αP,αK(P)) = D(P,K(P))
Это означает, что функция спроса однородна нулевой степени относительно всех цен и дохода.
Это есть свойство инвариантности спроса на пропорциональное повышение цен и дохода.
Замечание. Функция спроса, полученная в результате решения задачи (13.1), (13.2) удовлетворяет перечисленным свойствам.
Для функции спроса однородной нулевой степени объем потребления зависит не от абсолютных цен и дохода, от отношений цен (относительных цен) и отношения денежного дохода к цене (реальный доход).
Чувствительность спроса X*(P,K) на изменение цен и дохода оценивается с помощью соответствующих эластичностей.

Моделирование процессов потребления
Определение. Коэффициент эластичности спроса на товар i от цены на товар j есть:
Характеризует относительное изменение спроса по отношению к цене. Коэффициент эластичности показывает, на сколько процентов изменится спрос н i-ый товар, если цена на j-ый товар изменится на 1%.
Такая эластичность называется перекрестной.

Моделирование процессов потребления
Определение. Коэффициент эластичности спроса на товар i от цены на товар i:
Характеризует относительное изменение спроса по отношению к относительному изменению цены.
Коэффициент эластичности показывает на сколько процентов изменится спрос на i-ый товар при изменении цены на него на 1%.

Моделирование процессов потребления
Определение. Коэффициент эластичности спроса на товар i от дохода К есть:
Характеризует относительное изменение спроса по отношению к относительному изменению дохода.
Коэффициент эластичности показывает на сколько процентов изменится спрос на i-ый товар, если доход потребителя изменится на 1%.

Моделирование процессов потребления
Задача. Пусть функция полезности потребителя к двум товарам х и у – U(x,y)=xy. Вектор цен на товары P={px,py}, а доход потребителя К.
Найти предельные потребления и эластичности по ценам и доходу.
Система уравнений
Формализация задачи
Функция Лагранжа
Решение

Моделирование процессов потребления
Таким образом, функция спроса потребителя имеет вид:
Тогда: предельный спрос на товар х по ценам и доходу равен:
эластичности по ценам и доходу:

Моделирование процессов потребления
9. Анализ влияния цен и дохода на спрос.
Знаем, что для оценки различных ситуаций в сфере потребления применяются предельный спрос и предельная полезность денег по ценам и доходу: (∂xi/∂pi, ∂xi/∂K), (∂λ/∂pi, ∂λ/∂K).
Зная, что оптимальное решение задачи (13.1), (13,2) лежит на бюджетной линии, мы можем априори считать, что доход потребителя будет использован полностью. Тогда в (13.4)-(13.7) останутся только равенства:
K – (PX) = 0 (9.1)
∂U/∂X –λP = 0 (9.2)
Т.к система (9.1) и (9.2) зависит только от параметров P и K и содержит неизвестные X и λ, то эту систему можно представить в виде:
φ1(λ,Х,Р,К) = К-(РХ)
φ2(λ,Х,Р,К) = ∂U/∂X –λP
Т.к функция U дважды дифференцируема, непрерывна и удовлетворяет условиям ∂U/∂xi>0 и ∂2U/∂xi2<0, то система уравнений (9.1), (9.2) имеет решение, т.к. ее якобиан не равен нулю.

Моделирование процессов потребления
9. Анализ влияния цен и дохода на спрос.
9.1. Вычисление предельных величин ∂xi*/∂K и ∂λ*/∂K (влияние дохода на xi и λ).
Запишем (9.1), (9.2) в виде:
K – (PX*(P,K)) = 0 (9.3)
∂U(X*(P,K))/∂X –λ*(P,K)P = 0 (9.4)
Дифференцируем (9.3), (9.4) по К:
1-Р(∂X*/∂K) = 0
H(∂X*/∂K) –P(∂λ*/∂K) =0
В матричной форме эта система имеет вид:
(9.5)
Здесь:
Н – матрица Гессе;
∂Х*/∂K = {∂Х1*/∂K, ∂Х2*/∂K…}

Моделирование процессов потребления
9. Анализ влияния цен и дохода на спрос.
9.2. Вычисление предельных величин ∂xi*/∂pi и ∂λ*/∂pi (влияние цены pi при постоянстве остальных цен и дохода).
Дифференцируем (9.3) и (9.4) по pi и в координатной форме получим:
(9.6)
где δij – символ Кронеккера.
В матричной форме система уравнений (9.6) примет вид:
(9.7)

Моделирование процессов потребления
9. Анализ влияния цен и дохода на спрос.
9.3. Вычисление (∂xi*/∂pj)comp и (∂λ*/∂pj)comp (влияние цен на Х* и λ* при условии компенсации дохода и неизменности полезности).
Используя систему (9.1), (9.2), найдем полные дифференциалы функций U и K:
Условие неизменности полезности – dU=0
Откуда следует, что (P,dX)=0, т.к. λ≠0, и dK=(dPX)=dp1x1+dp2x2+…+dpnxn.
Экономически это означает, что при повышении цены pi до pi+dpi приращение дохода, обеспечивающее неизменность полезности, равно dK=dpixi.

Моделирование процессов потребления
9.3. Вычисление (∂xi*/∂pj)comp и (∂λ*/∂pj)comp (влияние цен на Х* и λ* при условии компенсации дохода и неизменности полезности).
Дифференцируя (9.3), (9.4) по pi с учетом dK=dpixi и (P,dX)=Σpi(∂xj*/∂pi)=0 получим:
В матричной форме полученная система уравнений имеет вид:
(9.8)

Моделирование процессов потребления
9.4. Основное уравнение теории потребления.
Три системы уравнений (9.6)-(9.8) можно объединить в одно:
(9.9)
Уравнение (9.9) называют основным матричным уравнением теории потребления.
Вторая матрица в левой части уравнения называется матрицей сравнительной статистики, а ее элементы – показателями сравнительной статистики.
Эти показатели характеризуют чувствительность X* и λ* к изменению параметров Р и К путем сравнения положения оптимума до и после изменения параметров.

Моделирование процессов потребления
9.5. Уравнение Слуцкого.
Основное матричное уравнение (9.9) можно записать в виде:
(9.10)
Решение этого уравнения относительно показателей сравнительной статистики по спросу имеет вид:
(9.11)
(9.12)
(9.13)

Моделирование процессов потребления
Можно показать, что μ=-(∂λ*/∂K)=-(∂2u*/∂K2)
Поэтому μ интерпретируют как коэффициент убывания предельной полезности денег.
Сравнивая (9.12) и (9.13), видно, что:
Сопоставляя последнее уравнение с (9.11), получим:
(9.14)
Уравнение (9.14) называют уравнением Слуцкого или основным уравнением теории ценности.
9.5. Уравнение Слуцкого.

Моделирование процессов потребления
9.5. Уравнение Слуцкого.
В координатной форме уравнение Слуцкого имеет вид:
(9.15)
Левую часть уравнения называют общим эффектом (от влияния цены на спрос).
Первое слагаемое в левой части – эффект замены (т.е. компенсированного изменения цены на спрос)
Второе слагаемое в левой части – эффект дохода (влияние изменения дохода на спрос).

Моделирование процессов потребления
9.5. Уравнение Слуцкого.
(9.16)
Перепишем уравнение (9.15) в следующем виде:
Из (9.11) следует, что матрица влияния замены симметрична и отрицательно определена, следовательно:
(9.17)
Экономически это означает, что компенсированное возрастание цены на товар приводит к уменьшению спроса на него.

Моделирование процессов потребления
9.5. Уравнение Слуцкого.
Из симметричности матрицы замены следует:
С учетом полученного, уравнение Слуцкого можно записать в виде:
(9.18)
Производная (∂xj*/∂pj называется влиянием на спрос (на товар j) изменения цены на этот товар.
Равенство (9.18) используется для классификации типов товаров.