Содержание
- 2. Первые упоминания о многогранниках известны еще за три тысячи лет до нашей эры в Египте и
- 3. … Евклид доказал, что существует именно 5 правильных многогранников
- 4. ЕВКЛИД, или ЭВКЛИД - древнегреческий математик, автор первых дошедших до нас теоретических трактатов по математике. Биографические
- 5. Геометрические знания примерно в объеме современного курса средней школы были изложены еще 2200 лет назад в
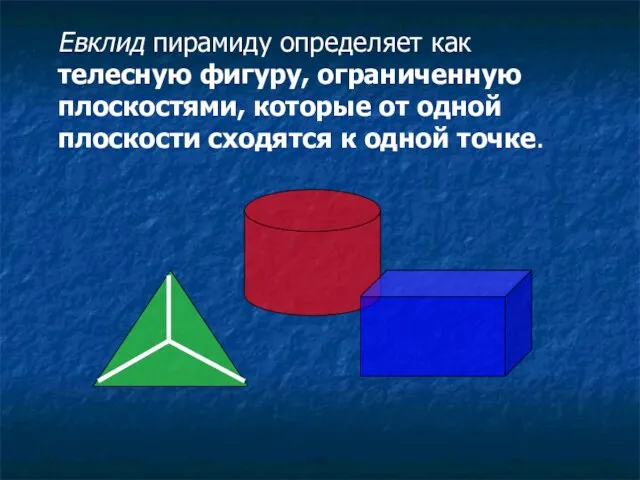
- 6. Евклид пирамиду определяет как телесную фигуру, ограниченную плоскостями, которые от одной плоскости сходятся к одной точке.
- 7. Додекаэдр
- 8. Икосаэдр
- 9. Правильный додекаэдр получается из куба построением «крыш» на его гранях, вершинами тетраэдра являются любые четыре вершины
- 11. Скачать презентацию
Слайд 2Первые упоминания о многогранниках известны еще за три тысячи лет до нашей
Первые упоминания о многогранниках известны еще за три тысячи лет до нашей

Слайд 3…
Евклид доказал,
что существует именно 5 правильных многогранников
…
Евклид доказал,
что существует именно 5 правильных многогранников

Слайд 4ЕВКЛИД, или ЭВКЛИД - древнегреческий математик, автор первых дошедших до нас теоретических
ЕВКЛИД, или ЭВКЛИД - древнегреческий математик, автор первых дошедших до нас теоретических

Известно также, что Евклид был моложе учеников Платона (427-347 до н. э.), но старше Архимеда (ок. 287-212 до н. э.), так как, с одной стороны, был платоником и хорошо знал философию Платона (именно поэтому он закончил "Начала" изложением так называемых платоновых тел, т. е. пяти правильных многогранников), а с другой стороны его имя упоминается в первом из двух писем Архимеда к Досифею "О шаре и цилиндре".
Слайд 5 Геометрические знания примерно в объеме современного курса средней школы были изложены
Геометрические знания примерно в объеме современного курса средней школы были изложены

Слайд 6Евклид пирамиду определяет как телесную фигуру, ограниченную плоскостями, которые от одной плоскости
Евклид пирамиду определяет как телесную фигуру, ограниченную плоскостями, которые от одной плоскости
Слайд 7Додекаэдр
Додекаэдр

Слайд 8Икосаэдр
Икосаэдр

Слайд 9Правильный додекаэдр получается из куба построением «крыш» на его гранях, вершинами тетраэдра
Правильный додекаэдр получается из куба построением «крыш» на его гранях, вершинами тетраэдра

 Федеральный государственный образовательный стандарт общего начального образования второго поколения
Федеральный государственный образовательный стандарт общего начального образования второго поколения Деструктивные организации
Деструктивные организации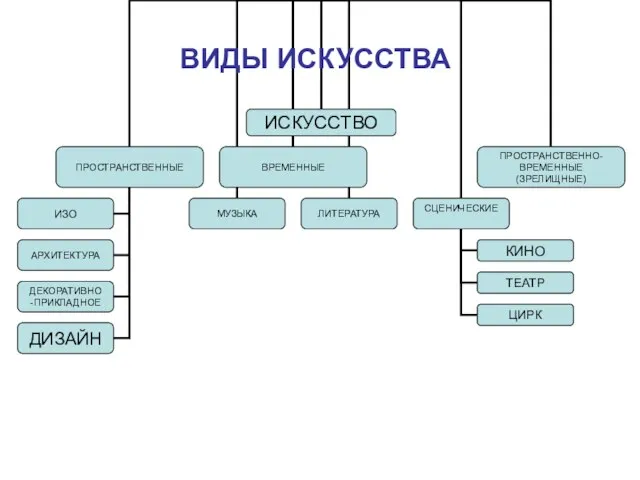 Виды искусства
Виды искусства Психоанализ и культура
Психоанализ и культура Основные законы управления
Основные законы управления Россия в XYIII столетии Россия при Петре I Российская империя как исторический феномен Эпоха дворцовых переворотов Россия при Екат
Россия в XYIII столетии Россия при Петре I Российская империя как исторический феномен Эпоха дворцовых переворотов Россия при Екат План недели Понедельник – Открытие недели начальных классов - День знатоков русского языка Вторник – Всероссийский конкурс по ма
План недели Понедельник – Открытие недели начальных классов - День знатоков русского языка Вторник – Всероссийский конкурс по ма 220 лет РГПУ им. А.И.Герцена
220 лет РГПУ им. А.И.Герцена Презентация на тему Что изучает современная экология?
Презентация на тему Что изучает современная экология?  Экспорт нефти и нормативно-правовое регулирование
Экспорт нефти и нормативно-правовое регулирование Векторная алгебра
Векторная алгебра Физическое развитие детей и подростков (2)
Физическое развитие детей и подростков (2) Презентация на тему Франциск 1
Презентация на тему Франциск 1 Основные виды организационных структур
Основные виды организационных структур Tunti 8. Ruoka
Tunti 8. Ruoka Гражданственность
Гражданственность Особенности региональной работы ЗПИФов недвижимости 27 ноября 2007
Особенности региональной работы ЗПИФов недвижимости 27 ноября 2007 Волейбол
Волейбол Факторы, оказывающие влияние на стоимость геодезических работ. Определение стоимости инженерно-геодезических изысканий
Факторы, оказывающие влияние на стоимость геодезических работ. Определение стоимости инженерно-геодезических изысканий МОУ СОШ №1 г.Краснознаменска урок МХК в 10 классе «Импрессионизм в живописи»
МОУ СОШ №1 г.Краснознаменска урок МХК в 10 классе «Импрессионизм в живописи» Презентация на тему Школьный референдум
Презентация на тему Школьный референдум Региональная инфраструктура сопровождения инновационных процессов в областной системе образования
Региональная инфраструктура сопровождения инновационных процессов в областной системе образования Русский народный праздник «Святки»
Русский народный праздник «Святки» Госбюджет. Внебюджетные фонды. Тема 6
Госбюджет. Внебюджетные фонды. Тема 6 Повышение эффективности системы поддержки научных исследований в интересах модернизации и инновационного развития оА.А. Фурсе
Повышение эффективности системы поддержки научных исследований в интересах модернизации и инновационного развития оА.А. Фурсе Доказательство теоремы Пифагора,основанного на теории подобия
Доказательство теоремы Пифагора,основанного на теории подобия Японская мифология
Японская мифология Научно-практическая конференция«Система взаимоотношений в теплоснабжении.Требования существующего и нового законодательства»
Научно-практическая конференция«Система взаимоотношений в теплоснабжении.Требования существующего и нового законодательства»