Некоторые свойства

Теорема. Медиана треугольника делит его на два равновеликих треугольника.
Обратное утверждение: «Если отрезок, соединяющий вершину треугольника с точкой противоположной стороны, делит данный треугольник на два равновеликих треугольника, то этот отрезок является его медианой».
Докажем, к примеру, обратное утверждение.

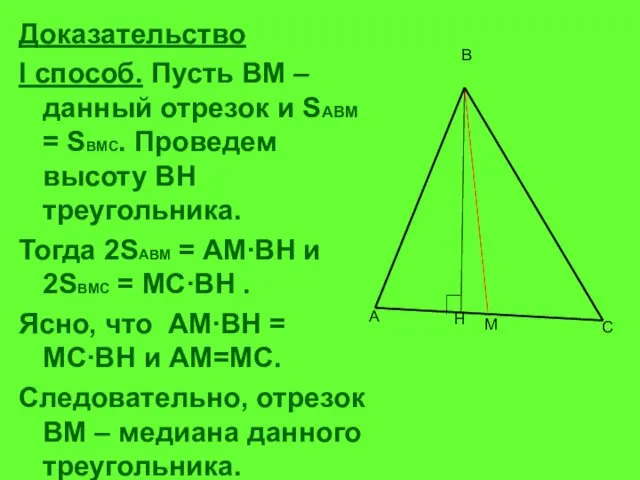
Доказательство
I способ. Пусть ВМ – данный отрезок и SABM = SBMC. Проведем высоту ВН треугольника.
Тогда 2SABM = AM∙ВH и 2SBMC = MC∙BH .
Ясно, что AM∙BH = MC∙BH и АМ=МС.
Следовательно, отрезок ВМ – медиана данного треугольника.

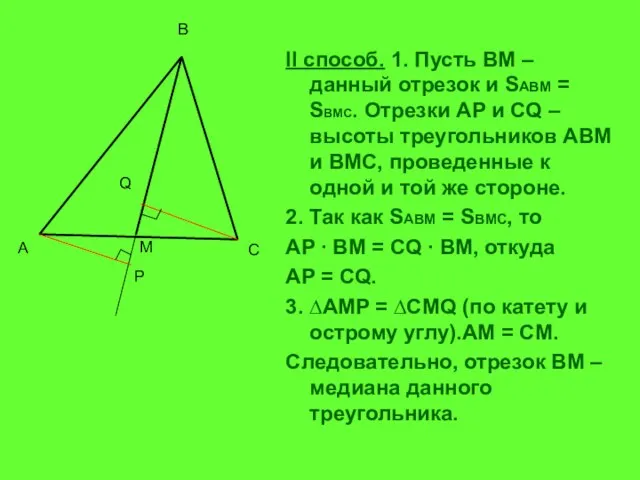
II способ. 1. Пусть ВМ – данный отрезок и SABM = SBMC. Отрезки AP и СQ – высоты треугольников АВМ и ВМС, проведенные к одной и той же стороне.
2. Так как SABM = SBMC, то
AP ∙ BM = CQ ∙ BM, откуда
AP = CQ.
3. ∆AMP = ∆CMQ (по катету и острому углу).AM = CM.
Следовательно, отрезок ВМ – медиана данного треугольника.

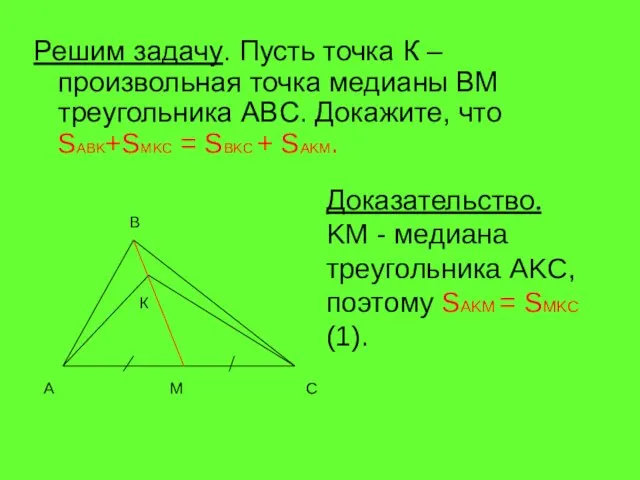
Решим задачу. Пусть точка К – произвольная точка медианы BM треугольника ABC. Докажите, что SABK+SMKC = SBKC + SAKM.
Доказательство.
KM - медиана треугольника AKC, поэтому SAKM = SMKC (1).

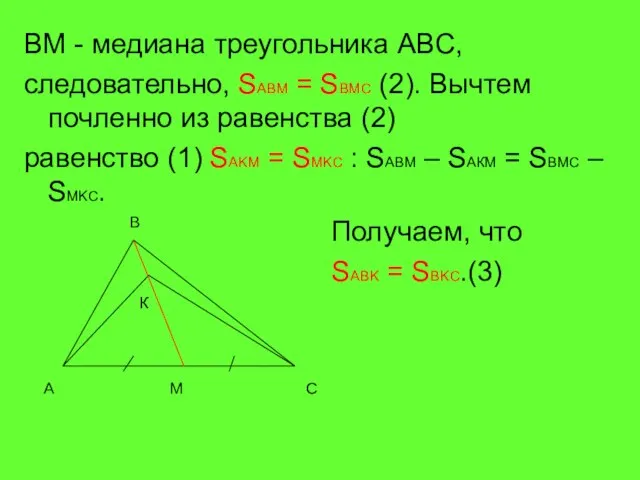
BM - медиана треугольника ABC,
следовательно, SABM = SBMC (2). Вычтем почленно из равенства (2)
равенство (1) SAKM = SMKC : SABM – SAКM = SBMC – SMKC.
Получаем, что
SABK = SBKC.(3)

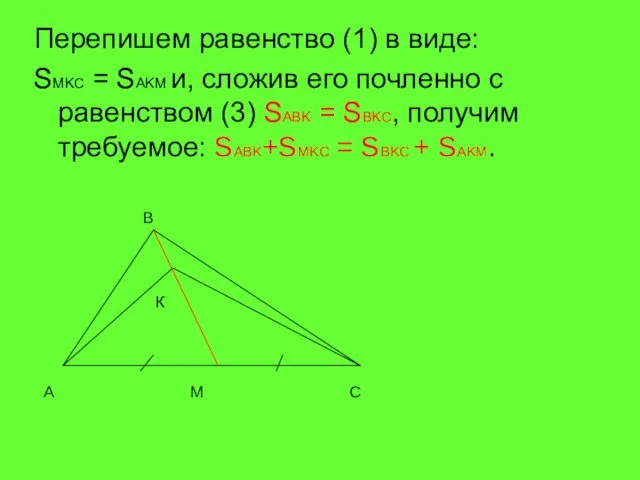
Перепишем равенство (1) в виде:
SMKC = SAKM и, сложив его почленно с равенством (3) SABK = SBKC, получим требуемое: SABK+SMKC = SBKC + SAKM.

Теперь докажем два утверждения.
Медианы треугольника пересекаются в одной точке и делятся этой точкой в отношении 2 : 1, считая от вершин, из которых они проведены.
Медианы треугольника, пересекаясь, делят его на шесть равновеликих треугольников.

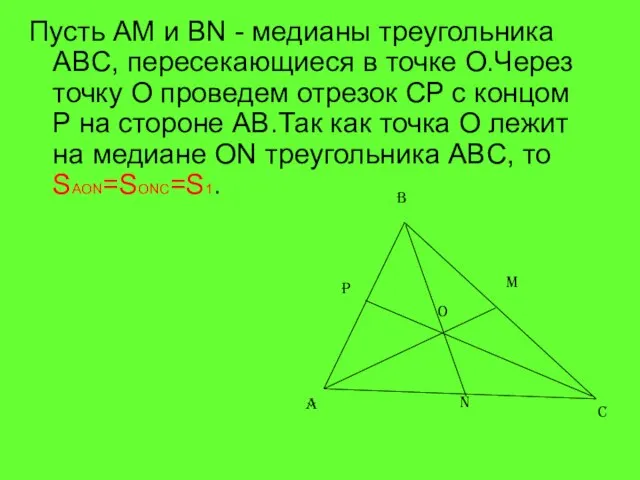
Пусть AM и BN - медианы треугольника ABC, пересекающиеся в точке О.Через точку O проведем отрезок CP с концом P на стороне AB.Так как точка O лежит на медиане ON треугольника ABC, то SAON=SONC=S1.

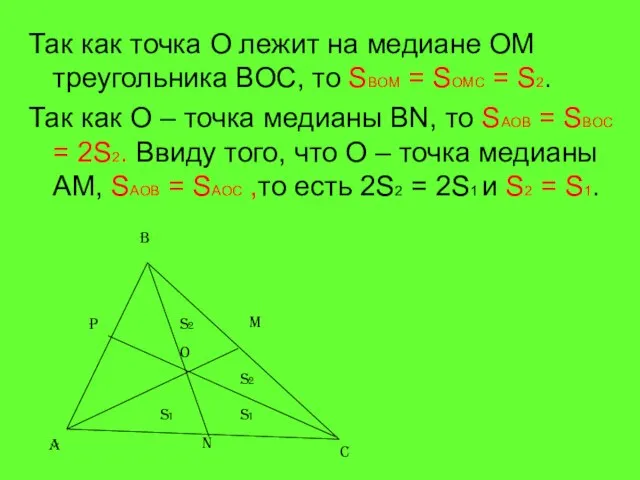
Так как точка О лежит на медиане ОМ треугольника ВОС, то SBOM = SOMC = S2.
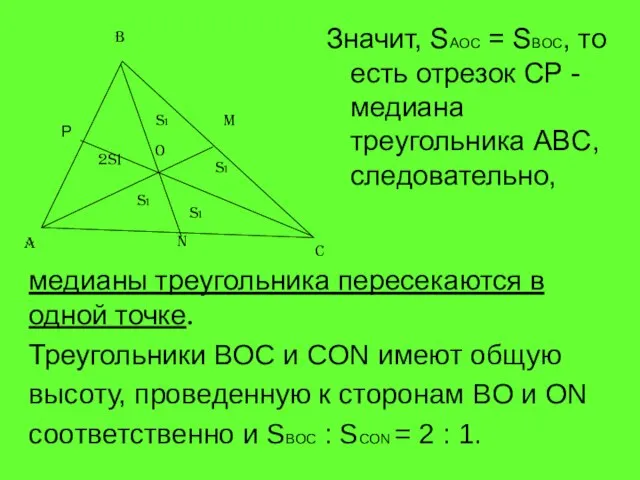
Так как О – точка медианы BN, то SAOB = SBOC = 2S2. Ввиду того, что О – точка медианы АМ, SAOB = SАOC ,то есть 2S2 = 2S1 и S2 = S1.

Значит, SAOC = SBOC, то есть отрезок CP - медиана треугольника ABC, следовательно,
медианы треугольника пересекаются в одной точке.
Треугольники BOC и CON имеют общую
высоту, проведенную к сторонам BO и ON
соответственно и SBOC : SCON = 2 : 1.