Содержание
- 2. Содержание Введение. Исходная система уравнений движения тяжелого сжимаемого газа со свободной поверхностью. Осредненная система уравнений –
- 3. 1. Статическая сжимаемость
- 4. 1. Применение
- 5. Уравнения движения Эйлера в поле силы тяжести Политропный совершенный сжимаемый газ, непрерывные процессы адиабатические. 2. Исходная
- 6. 3. Приближение мелкой воды.
- 7. 3. Осредненные уравнения по высоте
- 8. 4. Постановка задачи Римана.
- 9. 5. Решение Задачи Римана. Нахождение всех автомодельных непрерывных решений – центрированные волны Римана. Разрывные решения. Соотношения
- 10. 5. Непрерывные решения. Простые волны Римана Инварианты Римана Волны Римана, прямые характеристики
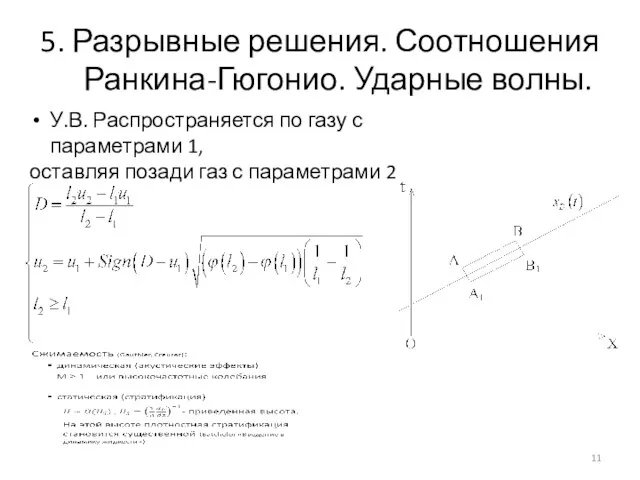
- 11. 5. Разрывные решения. Соотношения Ранкина-Гюгонио. Ударные волны. У.В. Распространяется по газу с параметрами 1, оставляя позади
- 12. 5. «Конструирование» решения по начальным условиям Система уравнений и интегральные следствия (соотношения Ранкина-Гюгонио) инвариантны относительно замены
- 13. 5. Автомодельное решение. две ударные волны
- 14. 5. Автомодельное решение. волна разрежения – ударная волна
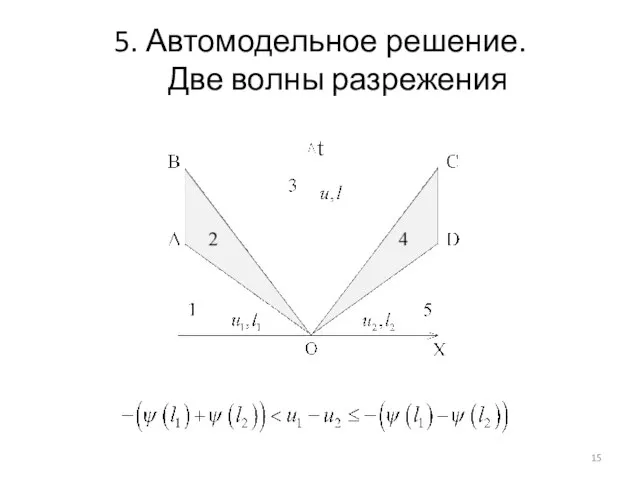
- 15. 5. Автомодельное решение. Две волны разрежения
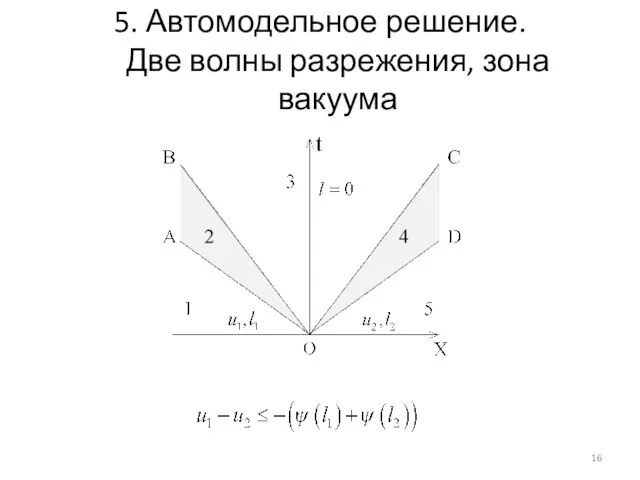
- 16. 5. Автомодельное решение. Две волны разрежения, зона вакуума
- 17. 6. Анализ результатов. Сравнение с классической мелкой водой.
- 18. 6. Анализ результатов. Сравнение с классической мелкой водой. Уменьшилась область начальных условий, при которых реализуется конфигурация
- 19. 6. Анализ результатов. Сравнение с классической мелкой водой. Увеличилась область начальных условий, при которых реализуется конфигурация
- 20. 7. Произвольная поверхность.
- 21. 7. Простые волны Римана. Простая волна – одно из уравнений выполняется тождественно во всей области Откуда
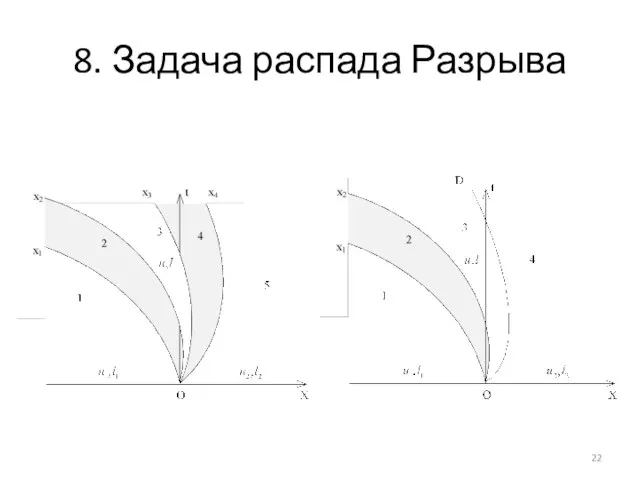
- 22. 8. Задача распада Разрыва
- 23. 9. Заключение Учет сжимаемости в мелкой воде приводит к улучшению предсказаний скорости распространения газового потока с
- 24. Спасибо за внимание!
- 25. Газ с твердыми частицами
- 26. Газ с твердыми частицами (Woods, 1995)
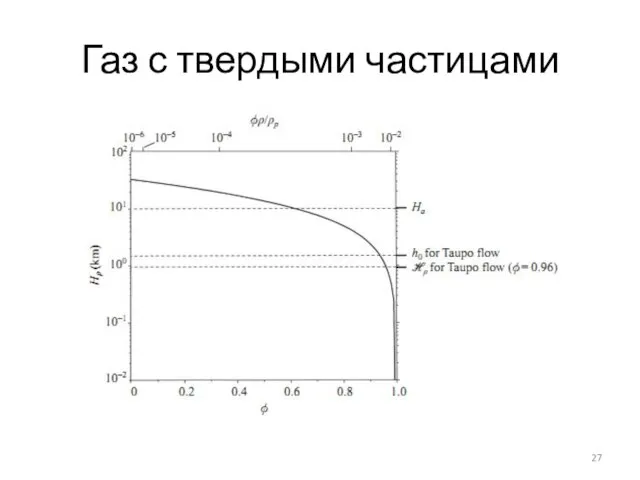
- 27. Газ с твердыми частицами
- 29. Скачать презентацию





















 Предквантум
Предквантум Старинные зимние обычаи и праздники, «Рождество», «Святки»
Старинные зимние обычаи и праздники, «Рождество», «Святки» ВИДЕО-СТЕНА DIBOSS LB-40
ВИДЕО-СТЕНА DIBOSS LB-40 Новый подход к интеграции календарно-сетевых графиков и смет
Новый подход к интеграции календарно-сетевых графиков и смет Областной конкурс Методическая разработка дистанционного урока - 2021
Областной конкурс Методическая разработка дистанционного урока - 2021 Музей путешествий. Поклонная гора. Парк Победы
Музей путешествий. Поклонная гора. Парк Победы Товары и услуги
Товары и услуги Техническое регулирование
Техническое регулирование 20140305_lekarstvennye_rasteniya_buturlinovskogo_rayona
20140305_lekarstvennye_rasteniya_buturlinovskogo_rayona Консолидация ритейла в Украине: роль логистики 1.Предпосылки для консолидации ритейла 2.Когда ритейлеру нужен 3PL-оператор? 3.Case study 4.
Консолидация ритейла в Украине: роль логистики 1.Предпосылки для консолидации ритейла 2.Когда ритейлеру нужен 3PL-оператор? 3.Case study 4. Project on the Indian Ocean
Project on the Indian Ocean  Портретная студийная съёмка
Портретная студийная съёмка Внешняя политика Советского государства 1920-х
Внешняя политика Советского государства 1920-х СТРОКА, ОБОРВАННАЯ ПУЛЕЙ
СТРОКА, ОБОРВАННАЯ ПУЛЕЙ ЕГЭ В 3 «Площади»
ЕГЭ В 3 «Площади» Цветовой контраст (хроматический)
Цветовой контраст (хроматический) Фотожурналист Владимир Вяткин
Фотожурналист Владимир Вяткин 26-27 апреля 2006 года Центр практической психологии РГУ имени С.А. Есенина Московский городской психолого-педагогический университе
26-27 апреля 2006 года Центр практической психологии РГУ имени С.А. Есенина Московский городской психолого-педагогический университе Кейс-стади для педагогов
Кейс-стади для педагогов Об аксиомах геометрии
Об аксиомах геометрии Презентация на тему Родная природа в стихотворениях поэтов xx века
Презентация на тему Родная природа в стихотворениях поэтов xx века  Каталог Атоми
Каталог Атоми Особенности организации и проведения школьного этапа Всероссийской олимпиады школьников по русскому языку Соловьева Т.В., предсе
Особенности организации и проведения школьного этапа Всероссийской олимпиады школьников по русскому языку Соловьева Т.В., предсе Создание новогодней открытки на основе пейзажа «Зимние россыпи»
Создание новогодней открытки на основе пейзажа «Зимние россыпи» Внесем порядок в хаос! ИЗО 7 класс
Внесем порядок в хаос! ИЗО 7 класс Космонавты, рожденные Украиной: космонавты Луганщины
Космонавты, рожденные Украиной: космонавты Луганщины Межрегиональный образовательный форум «Открытое образовательное пространство: живая праКтика тьюторства»
Межрегиональный образовательный форум «Открытое образовательное пространство: живая праКтика тьюторства» ДДК. Экскурсия
ДДК. Экскурсия