Содержание
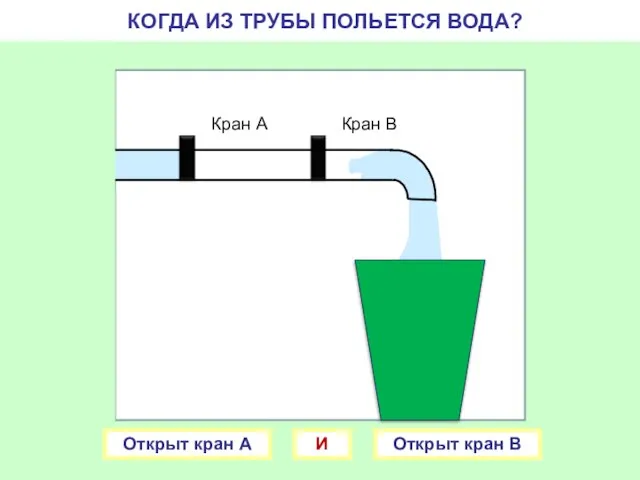
- 2. Кран В Кран А КОГДА ИЗ ТРУБЫ ПОЛЬЕТСЯ ВОДА? Открыт кран А Открыт кран В И
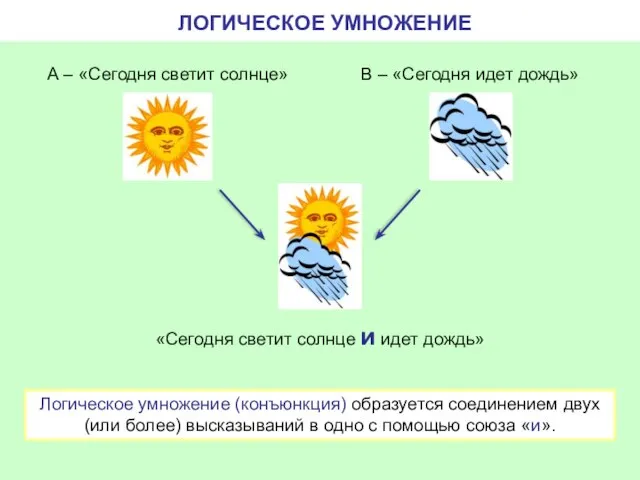
- 3. ЛОГИЧЕСКОЕ УМНОЖЕНИЕ «Сегодня светит солнце и идет дождь» А – «Сегодня светит солнце» В – «Сегодня
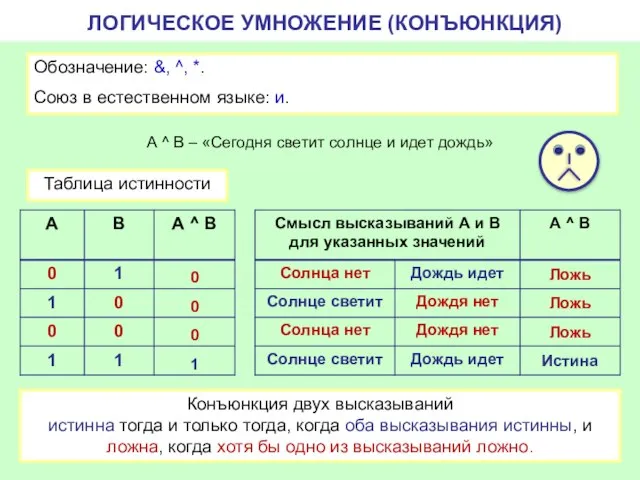
- 4. ЛОГИЧЕСКОЕ УМНОЖЕНИЕ (КОНЪЮНКЦИЯ) Обозначение: &, ^, *. Союз в естественном языке: и. А ^ B –
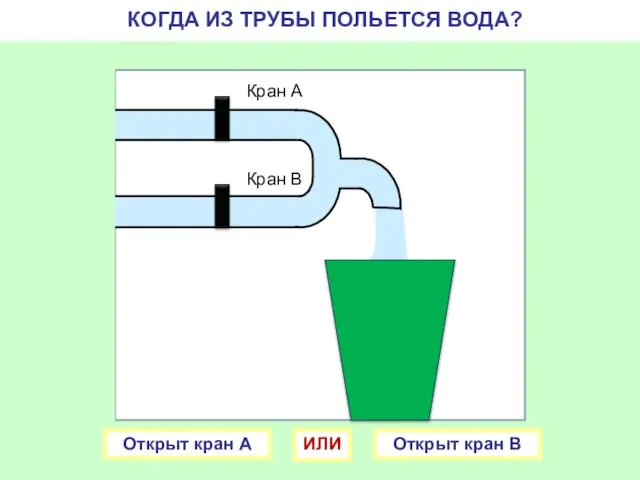
- 5. Кран А Кран В КОГДА ИЗ ТРУБЫ ПОЛЬЕТСЯ ВОДА? Открыт кран А Открыт кран В ИЛИ
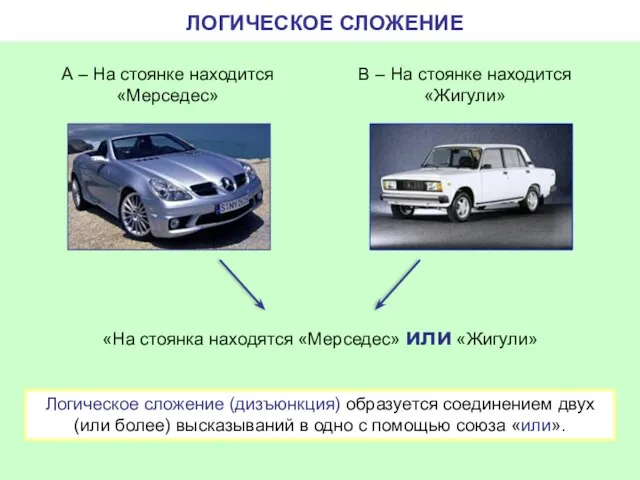
- 6. ЛОГИЧЕСКОЕ СЛОЖЕНИЕ «На стоянка находятся «Мерседес» или «Жигули» А – На стоянке находится «Мерседес» В –
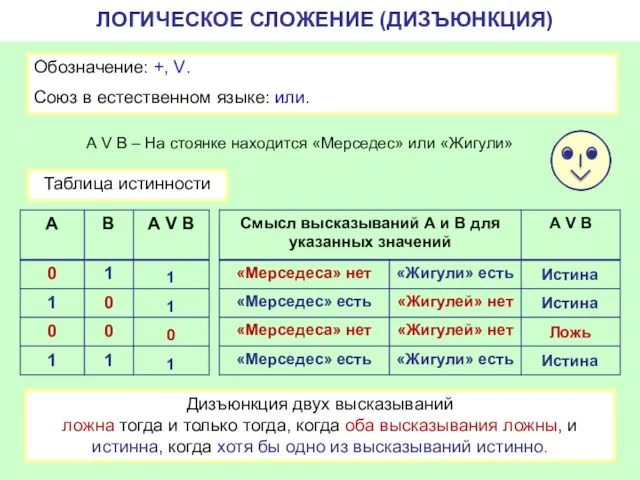
- 7. ЛОГИЧЕСКОЕ СЛОЖЕНИЕ (ДИЗЪЮНКЦИЯ) Обозначение: +, V. Союз в естественном языке: или. А V B – На
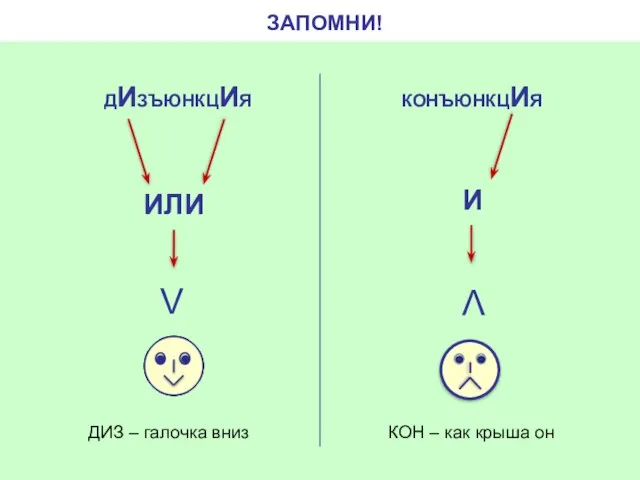
- 8. ЗАПОМНИ!
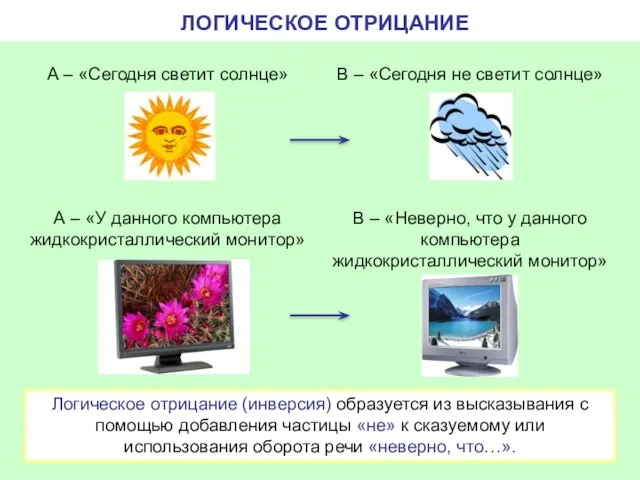
- 9. ЛОГИЧЕСКОЕ ОТРИЦАНИЕ А – «Сегодня светит солнце» В – «Сегодня не светит солнце» Логическое отрицание (инверсия)
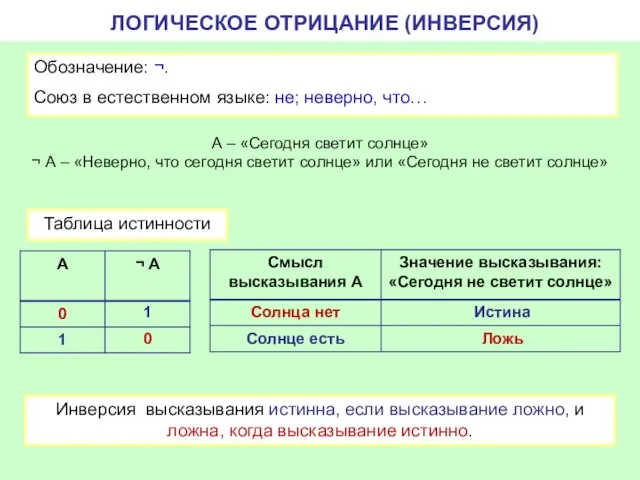
- 10. ЛОГИЧЕСКОЕ ОТРИЦАНИЕ (ИНВЕРСИЯ) Истина Ложь Обозначение: ¬. Союз в естественном языке: не; неверно, что… А –
- 11. ЛОГИЧЕСКОЕ СЛЕДОВАНИЕ Обозначение: →. Союз в естественном языке: если…, то…. Если на улице, то асфальт мокрый.
- 12. 1 0 1 1 Импликация двух высказываний ложна тогда и только тогда, когда из истинного высказывания
- 13. Обозначение: =, ↔, ~. Союз в естественном языке: тогда и только тогда, когда…. Число А –
- 15. Скачать презентацию



 Презентация на тему День дошкольного работника
Презентация на тему День дошкольного работника Республика Индия
Республика Индия Merged_document (2)
Merged_document (2) Деловые переговоры. Лекция №4
Деловые переговоры. Лекция №4 Presentation Title
Presentation Title  Стандартизация как инструмент обеспечения инновационной деятельности
Стандартизация как инструмент обеспечения инновационной деятельности Симметрия
Симметрия Художественный промысел лаковой миниатюры в поселке Холуй, Ивановской области
Художественный промысел лаковой миниатюры в поселке Холуй, Ивановской области Врожденные и приобретенные программы поведения
Врожденные и приобретенные программы поведения ЖратьСтвуйте!
ЖратьСтвуйте! Семья Перепечко
Семья Перепечко Раскол христианской церкви
Раскол христианской церкви Организация учебно-воспитательного процесса в общеобразовательных учебных заведениях и изучение базовых учебных дисциплин в осн
Организация учебно-воспитательного процесса в общеобразовательных учебных заведениях и изучение базовых учебных дисциплин в осн Презентация на тему Кукольный театр
Презентация на тему Кукольный театр Причины возникновения ураганов на территории южных районов Томской области
Причины возникновения ураганов на территории южных районов Томской области Классификация ресторанов в Латвии
Классификация ресторанов в Латвии Ф.И. Тютчев «Зима недаром злится»
Ф.И. Тютчев «Зима недаром злится» Презентация на тему Что такое Бенилюкс
Презентация на тему Что такое Бенилюкс Студенческая жизнь факультета ККП
Студенческая жизнь факультета ККП Приемная комиссия СПбГУ
Приемная комиссия СПбГУ Айс – Авто - одна из крупнейших оптово-розничных компаний в Санкт-Петербурге, занимающая 48%рынка в Северо-западном округе.
Айс – Авто - одна из крупнейших оптово-розничных компаний в Санкт-Петербурге, занимающая 48%рынка в Северо-западном округе. До тебя мне дойти не легко, а до смерти
До тебя мне дойти не легко, а до смерти «ЗДОРОВЫЕ ГЛАЗКИ, ДЕТСТВА ЯРКИЕ КРАСКИ»
«ЗДОРОВЫЕ ГЛАЗКИ, ДЕТСТВА ЯРКИЕ КРАСКИ» Тема: Истина и её критерии.
Тема: Истина и её критерии. Общественное объединение «СУТЯЖНИК»1994-2005
Общественное объединение «СУТЯЖНИК»1994-2005 Презентация на тему Вербное Воскресенье
Презентация на тему Вербное Воскресенье  Психолого – педагогическая служба в образовательном процессе
Психолого – педагогическая служба в образовательном процессе Земельный участок №2 под строительство ЦРБ в городе Бежецке
Земельный участок №2 под строительство ЦРБ в городе Бежецке