Неопределённость знаний и измерение информации

Содержательный подход к измерению информации
Количество информации в сообщении зависит от того, насколько новым является это сообщение для получателя.
Информации в сообщении будет тем больше, чем больше это сообщение пополняет наши знания.

Вероятностный подход
Пример 1:
Родители переживая за сына-студента, посылают ему телеграмму с вопросом об экзамене: «Сдал?».
В ответ приходит телеграмма: «Да!».
Посылая свою телеграмму, родители знали, что получат всего один из двух вариантов ответа – либо «да», либо «нет». Но какой именно, они не знали. Их неопределённость знания ответа была равна 2.

Пример 2:
Человек бросает монету, загадывая, что выпадет: орёл или решка.
Бросая монету, человек знает, что получит один из двух возможных вариантов. Его неопределённость знания результатов броска была равна 2. Ни один из этих вариантов не имеет преимущества перед другим.

В таких ситуациях, когда варианты событий не имеют друг перед другом преимущества, говорят, что события эти равновероятные.
Вероятность – это возможность того, что событие произойдёт.
Неопределённость знания о некотором событии – это количество возможных равновероятных результатов события.

Сообщение о том, что произошло одно событие из двух равновероятных, несёт 1 бит информации.
(Закодируем:
«да» или «нет» - «1» или «0»;
«орёл» или «решка» - «1» или «0»).
1 или 0

Примеры:
Подбрасывание монеты («орёл» или «решка») – неопределённость знаний равна 2, т.к. есть всего два возможных результата бросания.
Бросание игрального кубика - неопределённость знаний равна 6, т.к. кубик с шестью гранями может с равной вероятностью упасть на любую из них.

Формула Хартли
2i=N
N – число равновероятных событий
i – количество информации в сообщении

Не одинаковая вероятность
Пример:
В коробке имеется 50 шаров. Из них 40 белых и 10 чёрных.
Вероятность того, что при вытаскивании «не глядя» попадётся белый шар больше, чем вероятность попадания чёрного.
- вероятность попадания чёрного шара;
- вероятность попадания белого шара.

Расчёт количества информации
- вероятность события, где
K - количество интересующих нас событий,
N - общее число возможных исходов (событий) какого-то процесса.
Количество информации
или

В задаче о шарах определим количество информации в сообщении о попадании белого шара и чёрного шара:

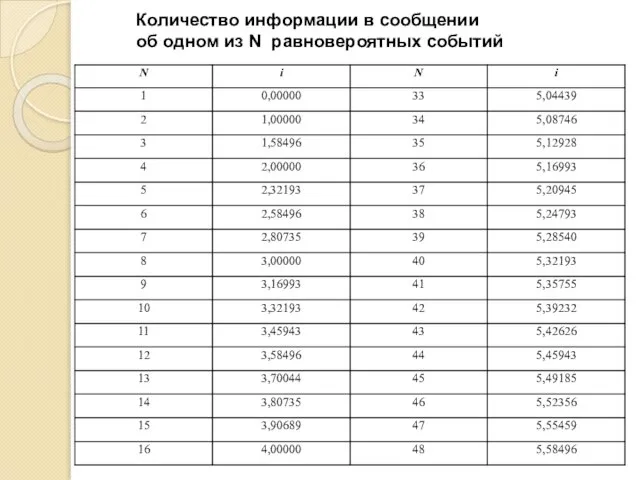
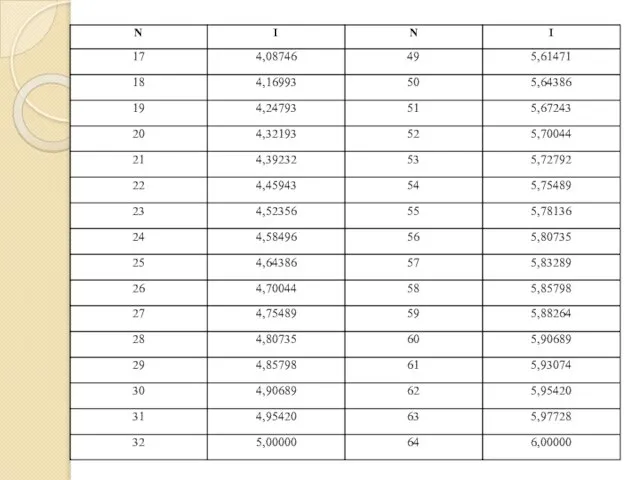
Количество информации в сообщении
об одном из N равновероятных событий