НЕТРАДИЦІИНІ СЕМАНТИКИ ЛОГІК КВАЗІАРНИХ ПРЕДИКАТІВ

Різновиди квазіарних предикатів
V-квазіарний предикат на A – це функція вигляду Р : VA → {T, F}
Область істинності та область хибності предиката Р:
T(P) = P–1(T) = {d∈ VA | T∈P(d)};
F(P) = P–1(F) = {d∈ VA | F∈P(d)}.
Якщо Р однозначний, то T(P)∩F(P) = ∅.
Якщо Р тотальний, то T(P)∪F(P) = VA.
Предикат P : VA → {T, F } назвемо:
– тотально істинним, якщо T(P) = VA;
– тотально хибним, якщо F(P) = VA;
– тотожно істинним, якщо T(P) = VA і F(P) = ∅;
– тотожно хибним, якщо T(P) = ∅ і F(P) = VA;
– тотально насиченим, якщо T(P) = F(P) = VA;
– неспростовним, або частково істинним, якщо F(P) = ∅;
– виконуваним, якщо T(P) ≠ ∅.

Предикат P : D→{T, F} монотонний, якщо d ⊆ d' ⇒ P(d) ⊆ P(d').
Окремим випадком монотонності є еквітонність – збереження прийнятого значення при розширенні даних.
Предикат P : D → {T, F} еквітонний, якщо
із P(d) ≠ ∅ та d ⊆ d′ випливає P(d′) = P(d).
Для однозначних предикатів монотонність стає еквітонністю.
Традиційне визначення еквітонного предиката:
Однозначний предикат P : D → {T, F} еквітонний, якщо
із P(d)↓ та d ⊆ d′ випливає P(d′)↓ = P(d).
Монотонність предиката означає, що прийняте ним значення зберігається при розширенні даних. Для однозначних часткових предикатів це може трактуватися як збереження "інформативності" предиката при збільшенні "інформативності" вхідних даних.

Для тотальних монотонних предикатів ситуація протилежна: при розширенні вхідних даних "інформативність" може тільки зменшуватися. Тому поняття монотонності малозмістовне для тотальних неоднозначних предикатів. Для них адекватним є дуальне поняття антитонності.
Предикат P : D → {T, F} антитонний, якщо d ⊆ d' ⇒ P(d) ⊇ P(d').
Якщо P антитонний, то P(∅) складається з усіх значень, які предикат може приймати на D, тобто P(∅) = EP .
Для тотальних неоднозначних предикатів антитонність означає: “інформативність” предиката не зменшується при збільшенні “інформативності” вхідних даних.
В класі однозначних предикатів антитонними можуть бути лише майже константні предикати: P(d) ≅ T для всіх d∈D або P(d) ≅ F для всіх d∈D.
В класі однозначних предикатів поняття антитонності малозмістовне.
Теорема 1. Композиції зберігають властивості еквітонності та антитонності.

Приклад. Розглянемо наступні предикати.
Р1 та Р2 тотальні однозначні немонотонні (нееквітонні) й неантитонні,
Р3 та Р5 монотонні (еквітонні) однозначні,
Р4 та Р6 монотонні тотальні неоднозначні,
Р7 та Р9 антитонні часткові однозначні,
Р8 та Р10 антитонні тотальні неоднозначні.

Φ неспростовна при інтерпретації на моделі мови A (позн. A |= Φ ), якщо ΦA – неспростовний (частково істинний) предикат.
Φ усюди (частково) істинна, або неспростовна ( позн. |= Φ ), якщо
A |= Φ для кожної моделі мови A.
Φ тотально істинна при інтерпретації на A ( позн. A |≡ Φ ), якщо
ΦA – тотально істинний предикат.
Φ тотально iстинна ( позн. |≡ Φ ), якщо A |≡ Φ ∀ моделі мови A.
Аналогічно даємо визначення тотожно істинної формули
та виконуваної формули
Ім'я x∈V строго неістотне для формули Φ:
x строго неістотне для ΦA ∀ моделі мови A
Для кожного р∈Ps множину синтетично строго неістотних предметних імен задамо за допомогою тотальної функції ν : Ps→2V,
Така функція продовжується до ν : Fr→2V .
Для семантичних моделей ЧКНЛ постулюється нескінченність множини тотально строго неістотних імен.

Модель мови АС B = (A, IB) дуальна до АС A = (A, IA): ∀ Φ∈Ps
Тоді A = (A, IA) дуальна до B = (A, IB).
A = (A, IA) – АС з частковими однозначними предикатами ⇒ дуальна B = (A, IB) – із тотальними неоднозначними предикатами, та навпаки.
Теорема. Нехай B = (A, IB) дуальна до A = (A, IA). Тоді ∀ Φ∈Fr:
1)
2) ΦA еквітонний ⇒ ΦB антитонний; ΦA антитонний ⇒ ΦB еквітонний.
Наслідок. ΦA неспростовний на АС A із частковими однозначними предикатами (неокласична семантика) ⇔ ΦB тотально істинний на дуальній АС B із тотальними неоднозначними предикатами (пересичена семантика).
Таким чином, неокласична семантика та пересичена семантика дуальні.

Теорема. 1. Для неокласичної семантики множина тотально істинних формул порожня.
2. Для пересиченої семантики множина неспростовних формул порожня.
3. Для загальної семантики множини тотально істинних і неспростовних формул порожні.
Неокласична семантика. Беремо модель мови A таку: кожний ПС інтерпретуємо як всюди невизначений предикат, на такій A кожна формула теж проінтерпретується як всюди невизначений предикат.
Пересичена семантика. Беремо модель мови В таку: кожний ПС інтерпретуємо як тотально насичений предикат, на такій В кожна формула теж проінтерпретується як тотально насичений предикат.
Загальна семантика. Беремо модель мови A і дуальну модель мови В.

Відношення логічного наслідку
Введемо 5 "природних" відношень логічного наслідку.
В різних семантиках вони мають різні властивості.
Задамо відношення наслідку для двох формул при інтерпретації на фіксованій моделі мови АС A.
1) "Істиннісний" наслідок A|=T : Φ A|=T Ψ ⇔ T(ΦA) ⊆ T(ΨA).
2) "Хибнісний" наслідок A|=F : Φ A|=F Ψ ⇔ F(ΨA) ⊆ F(ΦA).
3) "Cильний" наслідок A|=TF :
Φ A|=TF Ψ ⇔ T(ΦA) ⊆ T(ΨA) та F(ΨA) ⊆ F(ΦA).
4) "Неспростовнісний" наслідок A|=Cl : Φ A|=Cl Ψ ⇔ T(ΦA)∩F(ΨA) = ∅.
5) "Насичений" наслідок A|=Cm : Φ A|=Cm Ψ ⇔ F(ΦA)∪T(ΨA) = VA.
Відповідні відношення логічного наслідку: |=T , |=F , |=TF , |=Cl , |=Cm .
Їх визначаємо за такою схемою:
Φ |=* Ψ ⇔ Φ A|=* Ψ для кожної моделі мови A.

Відношення слабких наслідків
Ψ – слабкий логічний наслідок Φ (позн. Φ ||= Ψ), якщо ∀ моделі мови A маємо A |= Φ ⇒ A |= Ψ.
Ψ – слабкий тотальний наслідок Φ (позн. Φ ||≡ Ψ), якщо
∀ моделі мови A маємо A |≡ Φ ⇒ A |≡ Ψ.
Відношення |=T , |=F , |=TF , |=Cl , |=Cm , ||=, ||≡ рефлексивні й транзитивні.
Відношення логічного наслідку індукують відповідні відношення логічної еквівалентності. Такі відношення рефлексивні, транзитивні й си­метричні.
Відношення еквівалентності в АС A: A~T , A~F , A~TF , A~Cl , A~Cm
Відношення логічної еквівалентності: ~T , ~F , ~TF , ~Cl , ~Cm
Визначаємо їх за такою схемою:
Φ A~* Ψ, якщо Φ A|=* Ψ та Ψ A|=* Φ;
Φ ~* Ψ, якщо Φ |=* Ψ та Ψ |=* Φ.
Φ ~TF Ψ означає, що Φ та Ψ завжди інтерпретуються як один і той же предикат. Справді, для кожної моделі мови A
Φ A~TF Ψ ⇔ T(ΦA) = T(ΨA) та F(ΨA) = F(ΦA)

Теорема. Нехай АС B = (A, IB) дуальна до АС A = (A, IA). Тоді:
1) Φ A|=T Ψ ⇔ Φ B|=F Ψ та Φ A|=F Ψ ⇔ Φ B|=T Ψ;
2) Φ A|=Cl Ψ ⇔ Φ B|=Cm Ψ та Φ A|=Cm Ψ ⇔ Φ B |=Cl Ψ.
Наслідок. У випадку загальної семантики Φ |=T Ψ ⇔ Φ |=F Ψ ⇔ |=TF Ψ.
В загальній семантиці кожна АС B є дуальною до деякої АС A.
Теорема. Для кожної моделі мови A маємо:
1) Φ A|=T Ψ ⇔ ¬Ψ A|=F ¬Φ та Φ A|=F Ψ ⇔ ¬Ψ A|=T ¬Φ;
2) Φ A~T Ψ ⇔ ¬Ψ A~F ¬Φ та Φ A~F Ψ ⇔ ¬Ψ A~T ¬Φ.

У випадку неокласичної семантики немає жодної пари формул, які перебувають у відношенні |=Cm . Розглядаємо таку модель мови A, на якій усі ПС інтерпретуються як усюди невизначені предикати, тоді й усі формули на A інтерпретуються як усюди невизначені предикати.
У випадку пересиченої семантики немає жодної пари, які перебувають у відношенні |=Cl . Розглядаємо таку модель мови В, на якій усі ПС інтерпретуються як тотально насичені предикати, тоді й усі формули на В інтерпретуються як тотально насичені предикати.
У випадку загальної семантики немає жодної пари формул, які перебувають у відношенні |=Cl чи у відношенні |=Cm .
Загальна семантика. Маємо єдине природне змістовне відношення |=TF .
Неокласична семантика. Можна розглядати відношення |=T, |=F, |=TF, |=Cl.
Пересичена семантика. Можна розглядати відношення |=T, |=F, |=TF, |=Cm.

Поведінка введених відношень логічного наслідку вельми специфічна.
Теорема. У випадку неокласичної семантики маємо:
1) Φ & (Φ→Ψ) ||≡ Ψ; Φ ||= Ψ ∨ Φ&¬Ψ,
невірно Φ & (Φ→Ψ) ||= Ψ, невірно Φ ||≡ Ψ ∨ Φ&¬Ψ;
1) Φ & (Φ→Ψ) |=Cl Ψ, Φ |=Cl Ψ ∨ Φ&¬Ψ;
2) Φ & (Φ→Ψ) |=T Ψ, Φ & (Φ→Ψ) |≠F Ψ;
3) Φ |≠T Ψ ∨ Φ&¬Ψ; Φ |=F Ψ ∨ Φ&¬Ψ;
4) Φ ∨ Ψ&¬Ψ ~T Φ та невірно Φ ∨ Ψ&¬Ψ ~F Φ;
5) Φ&(Ψ∨¬Ψ) ~F Φ та невірно Φ&(Ψ∨¬Ψ) ~T Φ.
6) Φ&¬Φ |=TF Ψ∨¬Ψ; Φ & (Φ→Ψ) |=TF Ψ ∨ Φ&¬Ψ.
Теорема. У випадку пересиченої семантики маємо:
1) Φ & (Φ→Ψ) ||= Ψ, Φ ||≡ Ψ ∨ Φ&¬Ψ;
невірно Φ & (Φ→Ψ) ||≡ Ψ; невірно Φ ||= Ψ ∨ Φ&¬Ψ;
2) Φ & (Φ→Ψ) |=Cm Ψ, Φ |=Cm Ψ ∨ Φ&¬Ψ;
3) Φ & (Φ→Ψ) |≠T Ψ, Φ & (Φ→Ψ) |=F Ψ;
4) Φ |=T Ψ ∨ Φ&¬Ψ; Φ |≠F Ψ ∨ Φ&¬Ψ;
5) Φ ∨ Ψ&¬Ψ ~F Φ та невірно Φ ∨ Ψ&¬Ψ ~T Φ;
6) Φ&(Ψ∨¬Ψ) ~T Φ та невірно Φ&(Ψ∨¬Ψ) ~F Φ.
7) Φ&¬Φ |=TF Ψ∨¬Ψ; Φ & (Φ→Ψ) |=TF Ψ ∨ Φ&¬Ψ.

Теорема. У випадку загальної семантики:
1) Φ ||= Ψ ⇔ Φ ||≡ Ψ; 2) Φ & ¬Φ |≠TF Ψ ∨ ¬Ψ;
Φ & (Φ→Ψ) |≠TF Ψ ∨ Φ&¬Ψ.
Невірними будуть такі співвідношення:
Φ A|=T Ψ ⇒ ¬Ψ A|=T ¬Φ, ¬Ψ A|=T ¬Φ ⇒ Φ A|=T Ψ,
Φ A|=F Ψ ⇒ ¬Ψ A|=F ¬Φ, ¬Ψ A|=F ¬Φ ⇒ Φ A|=F Ψ.
Φ A~T Ψ ⇒ ¬Ψ A~T ¬Φ, ¬Ψ A~T ¬Φ ⇒ Φ A~T Ψ,
Φ A~F Ψ ⇒ ¬Ψ A~F ¬Φ, ¬Ψ A~F ¬Φ ⇒ Φ A~F Ψ.
Таким чином:
– для |=T та |=F закон контрапозиції невірний,
– для ~T та ~F не можна знімати заперечення в обох частинах еквівалентності.

Семантичні властивості логіки квазіарних предикатів
Використовуючи ~TF , можна описати властивості пропозиційних композицій та властивості, пов'язані з композицією реномінації й пропозиційними композиціями.
Наведемо для прикладу закони де Моргана:
¬(P∨Q) ~TF ¬P&¬Q; ¬(P&Q) ~TF ¬P∨¬Q.
Приклад. Існують АС A та формула Φ:
Φ A|=TF ∀xΦ та ∃xΦ A|≠Cl Φ, ∃xΦ A|≠Cm Φ.
Нехай Φ – це формула ∀x p → p для ПС p. Інтерпретуємо p на АС A так:
Маємо ∅ ⊂ T(pA) ⊂ VA, ∅ ⊂ F(pA) ⊂ VA, T(∀x pA) = VA, F(∀x pA) = ∅, T(∃x(∀x p → p)A) = VA, F(∃x(∀x p → p)A) = ∅, T(∀x(∀x p → p)A) = VA, F(∀x(∀x p → p)A) = ∅, ∅ ⊂ T((∀x p → p)A) ⊂ VA, ∅ ⊂ F((∀x p → p)A) ⊂ VA.
Звідси Φ A|=TF ∀xΦ, ∃xΦ A|≠Cl Φ, ∃xΦ A|≠Cm Φ.

Основні властивості, пов'язані з композиціями квантифікації.
Q1) ∃x∃yΦ ~TF ∃y∃xΦ та ∀x∀yΦ ~TF ∀y∀xΦ.
Q2) ¬∀xΦ ~TF ∃x¬Φ та ¬∃xΦ ~TF ∀x¬Φ.
Q3) ∃xΦ ~TF ∀x∃xΦ, ∃xΦ ~TF ∃x∃xΦ;
∀xΦ ~TF ∀x∀xΦ, ∀xΦ ~TF ∃x∀xΦ.
Q4) ∃xΦ∨∃xΨ ~TF ∃x(Φ∨Ψ) та ∀xΦ&∀xΨ ~TF ∀x(Φ&Ψ).
Q5) ∃x(Φ&Ψ)|=TF ∃xΦ&∃xΨ та ∀xΦ∨∀xΨ|=TF ∀x(Φ∨Ψ).
Q6) ∃y∀xΦ |=TF ∀x∃yΦ; водночас ∀x∃yΦ|≠* ∃y∀xΦ.
Q7) ∀xΦ |=* ∃xΦ; водночас ∀xΦ |≠* Φ, Φ |≠* ∀xΦ, Φ |≠* ∃xΦ.
Тут * – одне з Cl, Cm, T, F, TF.
Q8) Φ ||= ∃xΦ, Φ ||= ∀xΦ, ∀xΦ ||= ∃xΦ та Φ ||≡ ∃xΦ, Φ ||≡ ∀xΦ, ∀xΦ ||≡ ∃xΦ.

Для логік часткових однозначних предикатів додаємо властивості:
Q9P) |= ∀x (∀xΦ→Φ) та |= ∃x (∀xΦ→Φ);
|= ∀x (Φ→∃xΦ) та |= ∃x (Φ→∃xΦ);
Q10P) не завжди вірні |= Φ→∃xΦ, |=∀xΦ→Φ, ∀xΦ ||= Φ;
Q11P) для деяких формул Φ можливо: |= Φ→∀xΦ та невірно |= ∃xΦ→Φ.
Для логік тотальних неоднозначних предикатів додаємо властивості:
Q9) |≡ ∀x (∀xΦ→Φ) та |≡ ∃x (∀xΦ→Φ);
|≡ ∀x (Φ→∃xΦ) та |≡ ∃x (Φ→∃xΦ);
Q10Т) не завжди вірні |≡ Φ→∃xΦ, |≡∀xΦ→Φ, ∀xΦ ||≡ Φ;
Q11Т) для деяких формул Φ можливо:
|≡ Φ→∀xΦ та невірно |≡ ∃xΦ→Φ.

Теорема. 1) Для логік еквітонних предикатів
A|=Cl ∃xΦ та ∀xΦ A|=Cl ;
2) для логік антитонних предикатів
A|=Cm ∃xΦ та ∀xΦ A|=Cm ;
3) для логік еквітонних предикатів
A|=T ∃xΦ, ∀xΦ A|=F та ∀xΦ ||= ,
але вони не завжди вірні для логік антитонних предикатів;
4) для логік антитонних предикатів
A|=F ∃xΦ, ∀xΦ A|=T та ∀xΦ ||≡ ,
але вони не завжди вірні для логік еквітонних предикатів;
5) A|=TF ∃xΦ та ∀xΦ A|=TF не завжди вірні для логік еквітонних, так і для логік антитонних предикатів.

Для відношень ~Cl, ~Cm, ~TF справджується теорема семантичної еквiвалентності (тут * – одне з Cl, Cm, TF).
Теорема. Нехай формула Φ' отримана з Φ заміною деяких входжень формул Φ1, ..., Φn на Ψ1, ..., Ψn вiдповiдно.
Якщо Φ1 ~* Ψ1, ..., Φn ~* Ψn, то Φ ~* Φ'.
Для відношень ~T та ~F теорема невірна.
Справді, можливі ситуації:
– вірно Ξ ~T Φ та невірно ¬Ξ ~T ¬Φ, адже ¬Ξ ~T ¬Φ ⇔ Ξ ~F Φ;
– вірно Ξ ~F Φ та невірно ¬Ξ ~F ¬Φ.

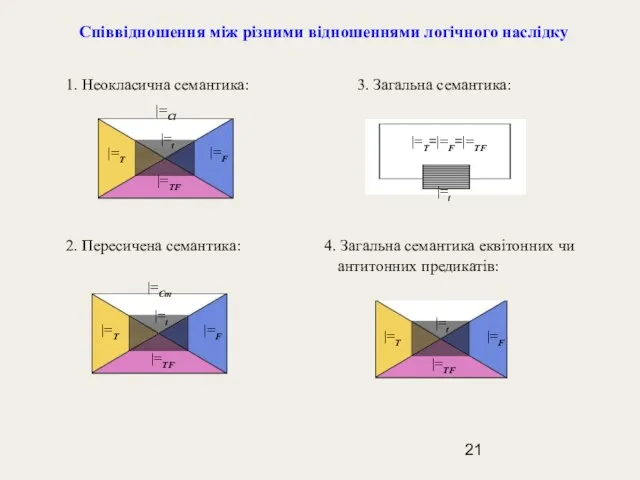
Співвідношення між різними відношеннями логічного наслідку
у відповідних семантиках
1. Неокласична семантика: |=TF ⊂ |=T , |=TF ⊂ |=F , |=T ⊂ |=Cl , |=F ⊂ |=Cl ;
|=t ⊂ |=Cl , |=F ⊂ ||=, |=T ⊂ ||≡; |=Cm = ∅;
|=t ⊄ |=T , |=t ⊄ |=F , |=TF ⊄ |=t ;
|=T ⊄ ||=, |=F ⊄ ||≡, ||= ⊄ |=Cl , ||≡ ⊄ |=Cl .
2. Пересичена семантика:
|=TF ⊂ |=T , |=TF ⊂ |=F , |=T ⊂ |=Cm , |=F ⊂ |=Cm ;
|=t ⊂ |=Cm , |=F ⊂ ||=, |=T ⊂ ||≡; |=Cl = ∅;
|=t ⊄ |=T , |=t ⊄ |=F , |=TF ⊄ |=t ;
|=T ⊄ ||=, |=F ⊄ ||≡, ||= ⊄ |=Cm , ||≡ ⊄ |=Cm .
3. Загальна семантика:
|=TF = |=T = |=F ; |=t ⊄ |=TF , |=TF ⊄ |=t ;
|=TF ⊂ ||≡ = ||= ; |=Cl = ∅, |=Cm = ∅.
4. Загальна семантика еквітонних чи загальна семантика антитонних:
|=TF ⊂ |=T , |=TF ⊂ |=F ; |=t ⊄ |=TF , |=TF ⊄ |=t ;
|=T ⊂ ||≡ , |=F ⊂ ||= ; |=Cl = ∅, |=Cm = ∅.

Співвідношення між різними відношеннями логічного наслідку
1. Неокласична семантика: 3. Загальна семантика:
2. Пересичена семантика: 4. Загальна семантика еквітонних чи
антитонних предикатів:

Відношення логічного наслідку для множин формул
Спочатку задамо відношення наслідку для множин формул при інтерпретації на фіксованій моделі мови АС A.
Нехай Γ⊆ Fr та Δ ⊆ Fr.
Γ A|=Cl Δ, якщо
Γ A|=Cm Δ, якщо
Γ A|=T Δ, якщо
Γ A|=F Δ, якщо
Γ A|=TF Δ, якщо
Відношення логічного наслідку для множин формул |=T , |=F , |=TF , |=Cl , |=Cm визначаємо за такою схемою:
Γ |=* Δ, якщо Γ A|=* Δ для кожної моделі мови A.
Відношення |=T , |=F , |=TF , |=Cl , |=Cm рефлексивні, але не транзитивні.

Теорема. Нехай АС B = (A, IB) дуальна до АС A = (A, IA). Тоді
1) Γ A|=T Δ ⇔ Γ B|=F Δ та Γ A|=F Δ ⇔ Γ B|=T Δ;
2) Γ A|=Cl Δ ⇔ Γ B|=Cm Δ та Γ A|=Cm Δ ⇔ Γ B|=Cl Δ.
Наслідок. У випадку загальної семантики
Γ A|=T Δ ⇔ Γ A|=F Δ ⇔ Γ A|=TF Δ.
У випадку загальної семантики природно розглядати лише |=TF .
Для неокласичної семантики можна розглядати |=T , |=F , |=TF , |=Cl ;
Для пересиченої семантики можна розглядати |=T , |=F , |=TF , |=Cm .
Теорема (заміни еквівалентних). Нехай Φ ~TF Ψ. Тоді:
Φ, Γ |=* Δ ⇔ Ψ, Γ |=* Δ та Γ |=* Δ, Φ ⇔ Γ |=* Δ, Ψ
Замість ~TF тут можна брати ~Cl чи ~Cm .
Тоді |=* буде відповідно лише відношенням |=Cl чи |=Cm .
Отримуємо ще дві різновидності теореми заміни еквівалентних
– для логіки часткових однозначних предикатів(із |=Cl );
– для логіки тотальних неоднозначних предикатів (із |=Cm ).

Основні властивості відношення |=
C) Якщо Γ∩Δ ≠ ∅, то Γ |= Δ.
U) Нехай Γ ⊆ Λ та Δ ⊆ Σ, тоді Γ |= Δ ⇒ Λ |= Σ.
¬¬ ) ¬¬Φ, Γ |= Δ ⇔ Φ, Γ |= Δ;
Γ |= Δ, ¬¬Φ ⇔ Γ |= Δ, Φ.
∨) Φ∨Ψ, Γ |= Δ ⇔ Φ, Γ |= Δ та Ψ, Γ |= Δ;
Γ |= Δ, Φ∨Ψ ⇔ Γ |= Δ, Φ, Ψ.
¬∨ ) ¬(Φ∨Ψ), Γ |= Δ ⇔ ¬Φ, ¬Ψ, Γ |= Δ;
Γ |= Δ, ¬(Φ∨Ψ) ⇔ Γ |= Δ, ¬Φ та Γ |= Δ, ¬Ψ.
Для |=Cl (неокласична семантика) та |=Cm (пересичена семантика):
¬) ¬Φ, Γ |= Δ ⇔ Γ |= Δ, Φ;
Γ |= Δ, ¬Φ ⇔ Φ, Γ |= Δ.
RT)
ΦU)

RR)
R¬)
R∨)
R∃R)
Зокрема,
R∃)
R∃∃)

На відміну від |=Cl та |=Cm, для |=T , |=F та |=TF не можна знімати заперечення, переносячи формулу з лівої частини у праву і навпаки, тому наведені властивості реномінації формулюємо і для зовнішнього заперечення:
¬RT)
¬ΦU)
¬RR)
¬R¬)
¬R∨)

¬R∃R)
Зокрема,
¬R∃)
¬R∃∃)

Розширення мови індикаторами наявності значення для змінних
Предикати εz – індикатори наявності в даному d∈VA значення для предметного імені z∈V – визначаємо так:
Теорема. Справджуються наступні співвідношення:
Як окремі випадки отримуємо:
Водночас невірними є такі співвідношення:

Властивості, пов'язані з елімінацією кванторів (використовують εx):
∃Rε|– )
∃ε |– )
за умови z∈VT та z∉nm(Γ, Δ, ∃хΦ).
∃Rv–| )
∃v–| )
Допоміжні властивості ε-розподілу:
εd) Γ |= Δ ⇔ εy, Γ |= Δ та Γ |= Δ, εy.
εv) Γ |= Δ ⇔ Γ |= Δ, εz за умови z∈VT та z∉nm(Σ).