ПЕРШОПОРЯДКОВІ ЧИСЛЕННЯ ГІЛЬБЕРТІВСЬКОГО ТИПУ НКЛ ПОВНОТОТАЛЬНИХ ЕКВІТОННИХ

ЧНКЧ – це трійка T = (L, Ax, P), де L – мова логіки із заданою множиною формул Fr, Ax ⊆ Fr – множина аксіом, P –правил виведення.
Ax розбита на множини Aлог логічних аксіом і Aвл власних аксіом.
Множина Aлог задається такими схемами аксіом:
АхПР) ¬Φ∨Φ
Ах∃∃) ∃x∃yΦ→∃y∃xΦ
АхR∃x)
АхR¬)
АхR∨)
АхRR)
АхRТ)
АхN∃) ∃xΦ→∀x∃xΦ
АхR∃)
АхNR)

АхNР) p→∀x p
Записані для всіх р∈Ps, АхNР визначають множини μ(p).
Множина P складається з відомих пропозиційних правил розширення, скорочення, асоціативності, перетину та кванторних правил:
П5) Φ→Ψ, Ψ→∀xΨ |– ∃xΦ→Ψ
Теорема істинності (коректності). T |– Ф ⇒ T |= Ф.
Доводиться теорема повноти чистих неокласичних числень:
Теорема повноти. T |= Φ ⇒ T |– Φ.
Ідея доведення – моделювання виведення квазізамкненої нормальної Ψ в численні T шляхом побудови виведення аналогічної їй формули класичної логіки Ψ' у відповідній теорії першого порядку ТΦ та навпаки

CЕКВЕНЦІЙНІ ЧИСЛЕННЯ НКЛ 1-ГО ПОРЯДКУ
Секвенційні числення – це формально-аксіоматичні системи, які формалізують відношення |= логічного наслідку для множин формул
Використовуємо модифіковану форму запису секвенцій.
Секвенції трактуємо як множини специфікованих формул
Кожна формула специфікована (відмічена) символом |- чи -|.
|- Φ – T-формула; -| Φ – F-формула.
Секвенції позначаємо |-Γ-| Δ.
Секвенційне числення будується так:
секвенція |-Γ-| Δ вивідна (має виведення) ⇔ Γ |= Δ.
Секвенція |-Γ-| Δ замкнена, якщо Γ∩Δ ≠ ∅.
Замкнені секвенції грають роль аксіом:
якщо |-Γ-| Δ замкнена, то Γ |= Δ.
Справді, Γ∩Δ ≠∅ ⇒ Γ |= Δ.

Секвенційні форми – синтаксичні аналоги семантичних властивостей відношення |=
Вони є правилами виведення секвенційних числень
Мають вигляд
Виведення в секвенційних численнях – дерево, вершини якого секвенції.
Індуктивне визначення секвенційного дерева:
1) Секвенція Σ утворює тривіальне сек. дерево з єдиною вершиною Σ
2) Нехай α – сек. дерево з коренем Σ, β – сек. дерево з коренем Υ,
– секвенційні форми. Тоді –
секвенційні дерева з коренем Ω.
Секвенційне дерево замкнене: кожний його лист – замкнена секвенція.
Секвенція Σ вивідна: існує замкнене сек. дерево з коренем Σ.
Таке замкнене дерево – виведення секвенції Σ.

Базові секвенційні форми НКЛ кванторного рівня

|−ΦN при у∈μ(A) −|ΦN при у∈μ(A)
|−R∃ −|R∃
Для |−R∃ та −|R∃ умова:
−|R∃∃ −|R∃∃
Для |−R∃∃, −|R∃∃ умови: z тотально неістотне,

При умові використовуємо форми |−R∃ та −|R∃,
При умові використовуємо форми |−R∃∃ та −|R∃∃.
|−∃ при у тотально неістотному та у∉nт(Σ, А)
−|∃
При застосуванні форми −|∃ {z1,…, zт} – це множина усіх імен множини доступних формул секвенції −|∃xА, Σ.
Секвенційне числення з цими базовими формами – QZN-числення
Теорема. Нехай − базові секв. форми, тоді
1) якщо Λ |= Κ, то Γ |= Δ; якщо Λ |= Κ та Χ |= Ζ, то Γ |= Δ.
2) якщо Γ |≠ Δ, то Λ |≠ Κ; якщо Γ |≠ Δ, то Λ |≠ Κ або Χ |= Ζ.

Поетапна процедура побудови дерева для секвенції Σ аналогічна відповідній процедурі для числень класичних чистих логік. 1-го порядку.
На початку побудови дерева зафіксуємо деякий нескінченний список TN тотально неістотних "нових" імен, які не зустрічаються в формулах секвенції Σ.
Кожне застосування секвенційної форми проводиться до скінченної множини доступних формул.
На початку кожного етапу виконується крок доступу: до списку доступних формул додається по одній зі списків |--формул та -|-формул.
На початку побудови дерева доступна лише пара перших формул списків.
Нехай виконано k етапів процедури. На етапі k+1 перевіряємо, чи буде кожен лист дерева замкненою секвенцією.
Якщо всі листи дерева замкнені, то процедура завершена позитивно, ми отримали замкнене секвенційне дерево.

Нехай існують незамкнені листи дерева.
Для кожного такого листа ξ робимо наступний крок доступу, після чого добудовуємо скінченне піддерево з вершиною ξ:
(1) Активізуємо всі доступні непримітивні формули ξ.
(2) По черзі до кожної активної формули застосовуємо відповідну секвенційну форму.
Форми |−RT, −|RТ, |−FN, −|FN допоміжні: перед застосуванням однієї з форм |−RR, −|RR, |−R¬, −|R¬, |−R∨, −|R∨, |−R∃, −|R∃, |−R∃∃, −|R∃∃ виконуємо за можливості спрощення, застосовуючи належну кількість раз ці форми |−RT, −|RТ, |−FN, −|FN.
Після застосування основної форми формула дезактивується.
Спочатку виконуємо всі |−∃-форми. При застосуванні |−∃ беремо у як перше незадіяне ім'я списку TN.

Після |−∃ виконуємо R∃∃-форми, при цьому беремо із задіяних імен списку TN, якщо це можливо, інакше z – перше незадіяне ім'я списку TN.
Потім до кожної з решти активних формул застосовуємо відповідну секвенційну форму |−¬, −|¬ , |−∨, −|∨, |−RR, −|RR, |−R¬, −|R¬, |−R∨, −|R∨, |−R∃, -|R∃, −|∃.
При застосуванні −|∃ множина {z1,…, zт} складається з усіх імен доступних формул листа та його наступників.
Всі повтори формул в секвенції усуваємо.
При побудові секвенційного дерева можливі такі випадки:
1) процедура завершена позитивно, маємо скінченне замкнене дерево;
2) процедура завершена негативно або не завершується, тоді маємо незамкнене скінченне або нескінченне дерево. У цьому випадку в дереві існує хоча б один незамкнений шлях ℘, його вершини – незамкнені секвенції, бо при появі замкненої до неї незастосовна жодна секвенційна форма, і процес побудови для цього шляху обривається. Кожна із формул секвенції Σ зустрінеться на шляху ℘ і стане доступною.

Теорема коректності. Нехай секвенція |−Γ−| Δ вивідна. Тоді Γ |= Δ.
Для доведення повноти QZN-числень – метод модельних множин.
Множина Н специфікованих формул із W = nm(Н) модельна, якщо:
HC)Для кожної примітивної Φ лишe одна з |−Φ чи −|Φ може належати Н
НN) Якщо ∈Н та у∈μ(Φ), то ∈Н ;
якщо ∈Н та у∈μ(Φ), то ∈Н .
Н¬) Якщо |−¬Φ∈Н, то −|Φ∈Н; якщо −|¬Φ∈Н, то |−Φ∈Н.
Н∨) Якщо |−Φ∨Ψ∈Н, то |−Φ∈Н або |−Ψ∈Н;
якщо −|Φ∨Ψ∈Н, то −|Φ∈Н та −|Ψ∈Н.
НT) Якщо ∈Н, то ∈Н;
якщо ∈Н, то ∈Н

HRR) Якщо ∈Н, то ∈Н;
якщо ∈Н, то ∈Н.
HR¬) Якщо ∈Н, то ∈Н;
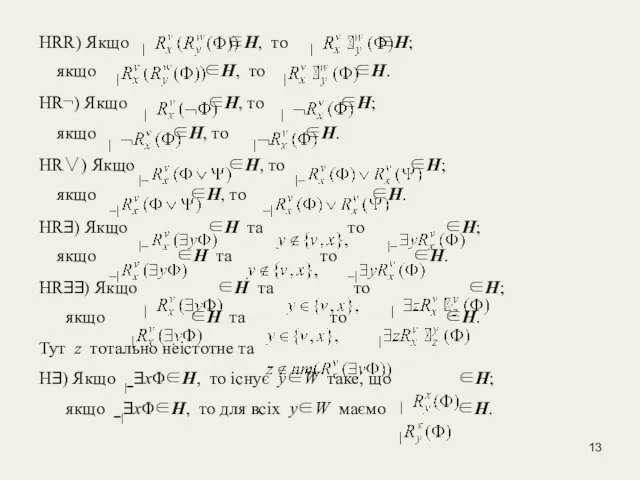
якщо ∈Н, то ∈Н.
HR∨) Якщо ∈Н, то ∈Н;
якщо ∈Н, то ∈Н.
HR∃) Якщо ∈Н та то ∈Н;
якщо ∈Н та то ∈Н.
HR∃∃) Якщо ∈Н та то ∈Н;
якщо ∈Н та то ∈Н.
Тут z тотально неістотне та
H∃) Якщо |−∃хΦ∈Н, то існує у∈W таке, що ∈Н;
якщо −|∃хΦ∈Н, то для всіх у∈W маємо ∈Н.

Теорема. Нехай ℘ – незамкнений шлях в секвенційному дереві, Н – множина всіх відмічених формул секвенцій цього шляху. Тоді Н – модельна множина.
Для переходу від нижчої вершини шляху до вищої використовується одна з базових секвенційних форм. Переходи згідно таких форм точно відповідають визначенню модельної множини. Кожна непримітивна формула шляху ℘ рано чи пізно буде розкладена чи спрощена згідно відповідної секвенційної форми. Всі секвенції шляху ℘ незамкнені.
Отже, Н − модельна множина
Теорема (про контрмодель). Нехай Н – модельна множина, нехай W=nт(Н).
Тоді існують АС А=(А, І) з |А|=|W| та ін'єктивна δ∈VA з im(δ)=W такі:
1) з умови |−Φ∈Н випливає ΦА(δ)=Т ;
2) з умови −|Φ∈Н випливає ΦА(δ)=F.
Візьмемо деяку А таку, що |А|=|W|, та ін'єктивну δ∈VA з im(δ)=W.
Доведення – індукцією за складністю формули згідно визначення модельної множини.

Спочатку задамо значення базових предикатів на δ та на ІМ вигляду
Якщо |-р∈Н, то рА(δ)=Т ; якщо -| р∈Н, то рА(δ)=F.
Якщо то візьмемо
Якщо то візьмемо
Так задані значення базових предикатів продовжимо, враховуючи умови неістотності імен, за еквітонністю на відповідні h∈VA.
Для всіх інших d∈VA значення рА(d) задаємо довільним чином, враховуючи еквітонність та обмеження стосовно неістотності:
∀ d, h∈VA таких, що d||-μ(p) = h||-μ(p), необхідно рА(d)=рА(h).
Для атомарних та формул вигляду твердження теореми випливають з визначення значень базових предикатів.

Доведемо крок індукції.
Нехай |-¬Φ∈Н. За визначенням Н маємо -|Φ∈Н. За припущенням індукції ΦА(δ)=F, звідки (¬Φ)А(δ)=Т.
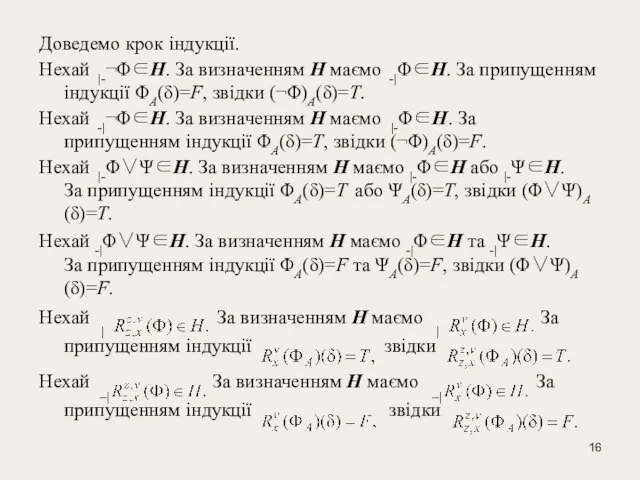
Нехай -|¬Φ∈Н. За визначенням Н маємо |-Φ∈Н. За припущенням індукції ΦА(δ)=Т, звідки (¬Φ)А(δ)=F.
Нехай |-Φ∨Ψ∈Н. За визначенням Н маємо |-Φ∈Н або |-Ψ∈Н. За припущенням індукції ΦА(δ)=Т або ΨА(δ)=Т, звідки (Φ∨Ψ)А(δ)=Т.
Нехай -|Φ∨Ψ∈Н. За визначенням Н маємо -|Φ∈Н та -|Ψ∈Н. За припущенням індукції ΦА(δ)=F та ΨА(δ)=F, звідки (Φ∨Ψ)А(δ)=F.
Нехай За визначенням Н маємо За припущенням індукції звідки
Нехай За визначенням Н маємо За припущенням індукції звідки

Нехай |−∃хΦ∈Н. За визначенням Н існує у∈W:
За припущенням індукції звідси
ΦA(δ∇хδ(у))=Т. Але δ(у)↓ згідно δ∈WА та у∈W, тому для а=δ(у) маємо ΦA(δ∇ха)=Т, звідки (∃хΦ)A(δ)=Т.
Нехай −|∃хΦ∈Н. За визначенням Н ∀у∈W. За припущенням індукції ∀у∈W. Звідси ΦA(δ∇хδ(у))=F ∀ у∈W. Згідно δ∈WА маємо δ(у)↓ ∀у∈W. Але δ – бієкція W→А, кожне b∈А має вигляд b=δ(у) для деякого у∈W. Отже, ΦA(δ∇хb)=F ∀ b∈А, звідки (∃хΦ)A(δ)=F.
Теорема повноти. Нехай Γ |= Δ. Тоді секвенція |−Γ−| Δ вивідна.
Прип. супротивне: Γ |= Δ та |−Γ−| Δ невивідна. Тоді секв. дерево δ для |− Γ−| Δ незамкнене ⇒ в δ існує незамкнений шлях ℘.
Нехай Н − множина всіх відмічених формул шляху ℘. Така Н − модельна множина. Звідси існують АС А=(А, І) та δ∈VA такі:
|−Φ∈Н ⇒ ΦА(δ)=Т та −|Φ∈Н ⇒ ΦА(δ)=F. Згідно з |−Γ−| Δ ⊆Н тоді Φ∈Γ ⇒ ΦА(δ)=Т та Φ∈Δ ⇒ ΦА(δ)=F. Це суперечить Γ |= Δ

Теорема компактності.
Cуперечливість та несуперечливість множин формул
Теорема 1 (ПК_1). Нехай Γ |= Δ. Тоді існують скінченні Γ0 ⊆Γ та Δ0 ⊆Δ такі, що Γ0 |= Δ0 .
Γ |= Δ ⇒ Σ = |−Γ−|Δ вивідна ⇒ Σ має скінченне замкнене секв.дерево δ, але в кожній вершині δ доступні скінченна к-ть формул секвенції.
Нехай ндΣ − множина всіх формул Σ, недоступних у вершинах δ. При побудові δ використовуються лише формули скінченної Σ0 = Σ\ндΣ. Відкинемо з кожної вершини δ всі формули ндΣ ⇒ дістанемо дерево δ0 з коренем Σ0 = |−Γ0 −|Δ0 , всі вершини якого − скінченні секвенції. Отже, Σ0 = |−Γ0 −|Δ0 вивідна ⇒ Γ0 |= Δ0
Γ синтаксично несуперечлива, якщо ∀ Φ |−Γ−|(Φ&¬Φ) невивідна.
Γ семантично несуперечлива (сумісна), якщо існують A=(А, I) та d∈VA такі: ΦА(d)=T ∀ Φ∈Γ.
Модель сумісності для Γ – АС A=(A, I) така: ∃ d∈VA: ΦА(d)=T ∀Φ∈Γ.
Γ семантично несуперечлива ⇔ Γ має модель сумісності.
Γ семантично несуперечлива ⇔ ∀ Φ маємо Γ |≠Φ&¬Φ

Теорема 2 (про існування моделі). Нехай Γ синтакс. несуперечлива. Тоді Γ має зліченну або скінченну модель сумісності.
Γ синт. несуперечлива ⇒ ∀ Φ секвенція Σ = |−Γ−|(Φ&¬Φ) невивідна ⇒ секв. дерево для |−Γ−|(Φ&¬Φ) незамкнене ⇒ в ньому існує незамкнений шлях ℘. Нехай Н − множина всіх формул секвенцій цього шляху ⇒ Н − модельна ⇒ існують АС А=(А, І) із скінченною або зліченною А та δ∈VA такі: |−Ψ∈Н ⇒ ΨА(δ)=Т та −|Ψ∈Н ⇒ ΨА(δ)=F. В силу Σ⊆Н це вірно і для формул з Σ = |−Γ−|(Φ&¬Φ) ⇒ ΨА(δ)=Т ∀ Ψ∈Γ ⇒ А=(А, І) − модель сумісності для Γ
Наслідок. Γ синтаксично несуп. ⇒ Γ семантично несуп.
Теорема 3. Γ семантично несуп. ⇒ Γ синтаксично несуп.
Прип. супротивне: Γ семант. несуп. та Γ синт. суп. ⇒ Γ |≠Ψ&¬Ψ ∀ Ψ та |− Γ−|(Φ&¬Φ) вивідна для деякої Φ ⇒ Γ |=Φ&¬Φ − суперечність
Наслідок 1. Γ синтаксично несуп. ⇔ Γ семантично несуп.
Надалі можна просто говорити про несуперечливість мн-ни формул Γ, не конкретизуючи, семантичну чи синтаксичну несуперечливість.
Наслідок 2. Γ синтаксично несуп. ⇔ Γ має модель сумісності.

Теорема 4 (аналог теореми Левенгейма Сколема↓). Γ має модель сумісності ⇒ Γ має зліченну або скінченну модель сумісності.
Γ має модель сумісності ⇒ Γ семан. несуп. ⇒ Γ синт. несуп. За теоремою 2 Γ має зліченну або скінченну модель сумісності
Теорема (ПК_2). Кожна скінченна Γ0 ⊆ Γ несуп. ⇒ Γ несуп.
Супротивне: кожна скінченна Γ0 ⊆ Γ несуп. та Γ суп. Тоді ∀ Φ |−Γ−|(Φ&¬Φ) вивідна ⇒ вона має скінченне замкнене секв. дерево δ. В кожній вершині дерева доступні тільки скінченна кількість формул секвенції, тому при побудові δ використані формули деякої скінченної Γ1 ⊆ Γ. Дістаємо дерево δ1 з коренем |−Γ1 −|(Φ&¬Φ), всі вершини якого − скінченні секвенції ⇒ |−Γ1 −|(Φ&¬Φ) вивідна ⇒ скінченна Γ1 ⊆ Γ суперечлива – отримали суперечність
Теорема (ПК_3). Кожна скінченна Γ0 ⊆ Γ має модель сумісності ⇒ Γ має модель сумісності.
Кожна скінченна Γ0 ⊆ Γ має модель сумісності ⇒ кожна така Γ0 несуп. За ПК_2 Γ несуперечлива ⇒ Γ має модель сумісності

Теорема (про взаємну суперечливість). Нехай Γ1 і Γ2 несуп. та Γ1∪Γ2 суп. Тоді існують скінченні Γ01 ⊆Γ1 та Γ02 ⊆Γ2 такі, що Γ01∪Γ02 суперечлива.
Γ1∪Γ2 суп. ⇒ існує скінченна суп. Γ0 ⊆ Γ1∪Γ2 (кожна скінченна Γ0 ⊆Γ1∪Γ2 несуп. ⇒ Γ1∪Γ2 несуп.). В силу несуп. Γ1 і Γ2 неможливо Γ0 ⊆Γ1 і Γ0 ⊆Γ2 . Отже, Γ0=Γ01∪Γ02 для деяких скінченних непорожніх Γ01 ⊆Γ1 та Γ02 ⊆Γ2
Теорема (про взаємну несуперечливість). Нехай Γ1 і Γ2 несуп. та для довільних Γ01 ⊆Γ1 і Γ02 ⊆Γ2 Γ01∪Γ02 несуп. Тоді Γ1∪Γ2 несуперечлива.
Супротивне: Γ1∪Γ2 суп. Тоді існує скінченна суперечлива Γ0 ⊆ Γ1∪Γ2 . Така Γ0 має вигляд Γ01∪Γ02 для деяких скінченних Γ01 ⊆Γ1 та Γ02 ⊆Γ2

Інтерполяційна теорема
Це олин із найважливіших результатів математичної логіки
Інтерполяційна теорема. Нехай секвенція –|Ψ→Ξ має виведення. Тоді існує Φ сигнатури σ(Φ)⊆σ(Ψ)∩σ(Ξ) така: –|Ψ→Φ та –|Φ→Ξ мають виведення.
Таку Φ називають інтерполяційною формулою, або інтерполянтом.
При σ(Ψ)∩σ(Ξ) = ∅ твердження теореми може бути невірним:
Нехай Ψ та Ξ – це ¬p∨p та ¬q∨q, де p, q∈Ps. Тоді інтерполянтом Φ буде всюди істинна формула, але при умові σ(Φ)⊆σ(Ψ)∩σ(Ξ) = ∅ такої Φ не існує, бо її просто немає з чого будувати.
Доводиться загальніше твердження (індукцією за довжиною виведення):
Теорема. Нехай Σ = Σ1, Σ2 має виведення δ ⇒ існує формула Φ сигнатури σ(Φ)⊆σ(Σ1)∩σ(Σ2) така, що за δ можна збудувати виведення δ1 для –|Φ, Σ1 та виведення δ2 для |–Φ, Σ2 .
Виведемо звідси інтерполяційну теорему
–|Ψ→Ξ має виведення ⇒ |–Ψ, –|Ξ має виведення. Візьмемо як Σ1 і Σ2 секвенції |–Ψ і –|Ξ. За теоремою існує Φ сигнатури σ(Φ)⊆σ(Ψ)∩σ(Ξ): –|Φ, |–Ψ та |–Φ, –|Ξ мають виведення. Звідси –|Ψ→Φ та –|Φ→Ξ мають виведення

Теореми про визначність
Розглянемо співвідношення між двома різними уточненнями визначення одного поняття в термінах інших понять.
Одне уточнення – семантичне, або неявне. Його суть: поняття (ПС) q неявно визначається через поняття p1,…, pn в теорії (множині формул) Γ, якщо для кожних моделей істинності Γ, узгоджених у тому розумінні, що в них p1,…, pn інтерпретуються однаково, маємо однакові інтерпретації для q.
Друге – синтаксичне, або явне. Його суть: поняття q явно визначається в Γ через p1,…, pn, якщо таке визначення є логічним наслідком Γ.
Для класичної логіки еквівалентність явного та неявного визначення одного поняття в термінах інших – це теорема Бета про визначність.
Нехай π⊆Ps – деяка множина предикатних символів мови.
Модель істинності для Γ – це A=(A, I) така: ∀d∈VA ∀Φ∈Γ ΦА(d) ≅ T.
Для логік ПЕП кожна модель істинності є моделлю сумісності. Для логік ЕП це невірно: розгл. АС, де кожний ПС інтерпретується як усюди невизначений предикат
Моделі істинності A=(M, IA) та В=(M, IВ) мн-ни формул Γ π-тотожні, якщо ∀ p∈π маємо pA ≅ pВ .