Содержание
- 2. Katedra kybernetiky a umelej inteligencie FEI, TU v Košiciach /8 Osnova prednášky Spracovanie neurčitých znalostí Neurčitosť
- 3. Katedra kybernetiky a umelej inteligencie FEI, TU v Košiciach /8 1. Spracovanie neurčitých znalostí Iba malá
- 4. Katedra kybernetiky a umelej inteligencie FEI, TU v Košiciach /8 2. Neurčitosť v BZ a v
- 5. Katedra kybernetiky a umelej inteligencie FEI, TU v Košiciach /8 3. Delenie neurčitosti Neurčitosť znalostí má
- 6. Katedra kybernetiky a umelej inteligencie FEI, TU v Košiciach /8 4. Reprezentácia neurčitosti SYMBOLICKÁ Reprezentácia slovným
- 7. Katedra kybernetiky a umelej inteligencie FEI, TU v Košiciach /8 5. Modely práce s neurčitosťou Model
- 9. Скачать презентацию
Слайд 2Katedra kybernetiky a umelej inteligencie FEI, TU v Košiciach
/8
Osnova prednášky
Spracovanie neurčitých znalostí
Neurčitosť
Katedra kybernetiky a umelej inteligencie FEI, TU v Košiciach
/8
Osnova prednášky
Spracovanie neurčitých znalostí
Neurčitosť

Delenie neurčitosti
Reprezentácia neurčitosti
Modely práce s neurčitosťou
Všeobecný extenzionálny model
Слайд 3Katedra kybernetiky a umelej inteligencie FEI, TU v Košiciach
/8
1. Spracovanie neurčitých znalostí
Katedra kybernetiky a umelej inteligencie FEI, TU v Košiciach
/8
1. Spracovanie neurčitých znalostí

ALGORITMUS. Jednoznačný výpočtový postup vedúci k optimálnemu riešeniu. Vyznačuje sa hromadnosťou, konečnosťou a resultatívnosťou..
HEURISTIKA. Je neformálny úsudkový postup, osvedčený v dostatočnom počte prípadov (nedokázateľný ale použiteľný). Nezaručuje hromadnosť ani optimál. riešenia.
Znalosti o neurčitosti (4. typ znalostí): sú panoramatické, lebo sa týkajú tak predmetných, konkrétnych znalostí ako aj metaznalostí. Vyjadrujú mieru istoty experta vo výsledok.
Слайд 4Katedra kybernetiky a umelej inteligencie FEI, TU v Košiciach
/8
2. Neurčitosť v BZ
Katedra kybernetiky a umelej inteligencie FEI, TU v Košiciach
/8
2. Neurčitosť v BZ

NEURČITOSŤ v BZ. Dôležitá súčasť ES založenom na vedomostiach experta (jeho skúsenosti, domienky, mentálne modely, nie celkom exaktné znalosti, nie rigorózne tvrdenia, osvedčené postupy).
NEURČITOSŤ v BD. Neisté odpovede používateľa, subjektívnosť úsudku používateľa, odhady nedostupných informácií (vysoké náklady), nepresné, zašumené dáta.
Pomocou inferencie sa neurčitosť šíri po inferenčnej sieti.
Слайд 5Katedra kybernetiky a umelej inteligencie FEI, TU v Košiciach
/8
3. Delenie neurčitosti
Neurčitosť
Katedra kybernetiky a umelej inteligencie FEI, TU v Košiciach
/8
3. Delenie neurčitosti
Neurčitosť

NEKOMPLETNOSŤ spočíva vo fragmentálnosti ľudských poznatkov (človek: predpoklady o svete, všeobecné pravidlá). Znalosti sú podmienečne platné, revidovateľné. Kvantifikátory: väčšinou, veľmi, všeobecne, typicky.
VÁGNOSŤ – znalosti sú zdieľané pomocou slov s nejednoznačným významom: vysoký, starý. Pridaním kvatifikátorov narastá: veľmi starý, obvykle vysoký.
NEURČITOSŤ odráža subjektívny charakter ľudských znalostí (heuristiky, odhady, skúseností, neznalosť súvislostí, povrchnosť, predpojatosť, sebadôvera).
Delenie: možnosť externá subjektívna
plausibilnosť interná objektívna
Слайд 6Katedra kybernetiky a umelej inteligencie FEI, TU v Košiciach
/8
4. Reprezentácia neurčitosti
SYMBOLICKÁ
Reprezentácia slovným
Katedra kybernetiky a umelej inteligencie FEI, TU v Košiciach
/8
4. Reprezentácia neurčitosti
SYMBOLICKÁ
Reprezentácia slovným

NUMERICKÁ
Reprezentácia numerickou hodnotou. Nepoznáme pôvod neurčitosti, ale dokážeme odvodiť neurčitosť novej znalosti.
Numerická reprezentácia podľa počtu hodnôt:
Jedno-hodnotová
Viac-hodnotová: dôvera a nedôvera sa vyjadrujú zvlášť a sú si doplnkom navzájom (konfidenčný interval, činiteľ istoty).
Numerická reprezentácia podľa absolútnosti vyjadrenia:
Absolútna: p=0.8=80%, <0,1>, <-1,1>
Relatívna: zmena neurčitosti záveru v prípade splnenia jeho predpokladu (šanca, činiteľ istoty, miera postač. a nezbyt.)
Слайд 7Katedra kybernetiky a umelej inteligencie FEI, TU v Košiciach
/8
5. Modely práce s
Katedra kybernetiky a umelej inteligencie FEI, TU v Košiciach
/8
5. Modely práce s

Model práce s neurčitosťou predstavuje pravidlá, podľa ktorých sa neurčitosť šíri cez inferenčnú sieť. Modely delíme na:
INTENZIONÁLNE: Riešia problém globálne. Uvažujú o všetkých závislostiach medzi znalosťami. Vo všeobecnosti nie je možná žiadna kombinačná funkcia (obtiažna modifikovateľnosť, dlhé odvádzanie, teoretická správnosť).
EXTENZIONÁLNE: Sú založené na princípe lokálnosti (extenzionality). Predpokladajú existenciu kombinačných funkcií (rýchlosť, jednoduchosť, modifikovateľnosť, implementovateľnosť, nezabezpečujú teoretickú správnosť).
Princíp extenzionality: pravdivostná hodnota výroku je určená pravdivostnými hodnotami jeho zložiek a nezávisí od platnosti výrokov, ktoré nie sú jeho súčasťou.
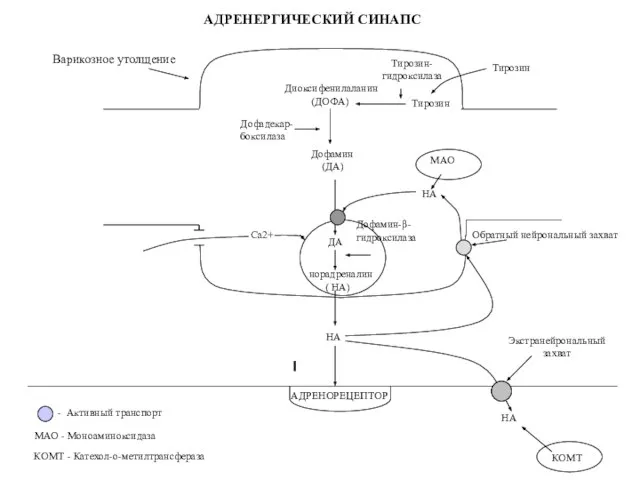 Адреномиметики
Адреномиметики Sport in Canada
Sport in Canada АО Вюрт Северо-Запад, Санкт-Петербург. Боулинг–турнир. Месяц новых клиентов
АО Вюрт Северо-Запад, Санкт-Петербург. Боулинг–турнир. Месяц новых клиентов Презентация на тему Русский герой сказок: Иван-дурак
Презентация на тему Русский герой сказок: Иван-дурак  Путешествие на водопад Атыш
Путешествие на водопад Атыш Помада Creamy Glam
Помада Creamy Glam Презентация по английскому Королевская семья Великобритании
Презентация по английскому Королевская семья Великобритании tema-gribi-rodnaya-tropinka_ru
tema-gribi-rodnaya-tropinka_ru Работа социального педагога с детьми имеющих отклоняющее поведение.
Работа социального педагога с детьми имеющих отклоняющее поведение. Комплекс упражнений утренней гимнастики
Комплекс упражнений утренней гимнастики Службы для электронного общения
Службы для электронного общения Характер и темперамент
Характер и темперамент Обществознание
Обществознание Материально-техническая база одно из условий эффективной реализации профильного обучения.
Материально-техническая база одно из условий эффективной реализации профильного обучения. Способ тепловой обработки сыпучих материалов и устройства для его осуществления
Способ тепловой обработки сыпучих материалов и устройства для его осуществления Архитектура Санкт-Петербурга
Архитектура Санкт-Петербурга project
project Greenway. Жизнь без химии с заботой о семье и природе
Greenway. Жизнь без химии с заботой о семье и природе Адрес: Тверская область, г. Нелидово Ул. Шахтерская 16
Адрес: Тверская область, г. Нелидово Ул. Шахтерская 16 Сказочные птицы
Сказочные птицы Леонардо Да Винчи
Леонардо Да Винчи Как преодолеть стресс перед экзаменом
Как преодолеть стресс перед экзаменом Признаки нарушения адаптации в почерке
Признаки нарушения адаптации в почерке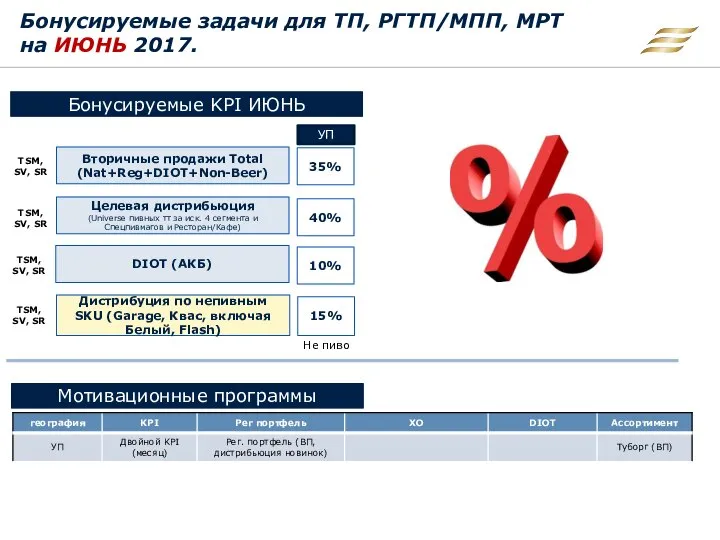 Бонусируемые задачи для ТП, РГТП/МПП, МРТ на июнь 2017
Бонусируемые задачи для ТП, РГТП/МПП, МРТ на июнь 2017 Доходы предприятия и финансовые результаты его деятельности
Доходы предприятия и финансовые результаты его деятельности Алтайский государственный университет
Алтайский государственный университет Методика оформление. Пушкинская карта
Методика оформление. Пушкинская карта Презентация на тему Социальная информатика
Презентация на тему Социальная информатика