Нормализация отношений

Аномалии модификации данных
При неправильно спроектированной схеме реляционной БД могут возникнуть аномалии выполнения операций модификации данных.
Рассмотрим эти аномалии на примере следующего отношения:
ПОСТАВКИ (Номер поставки, Название товара, Цена товара, Количество, Дата поставки, Название поставщика, Адрес поставщика)
Различают аномалии обновления, удаления и добавления.
Аномалия обновления может возникнуть в том случае, когда информация дублируется. Другие аномалии возникают тогда, когда две и более сущности объединены в одно отношение.
Например:
Аномалия обновления: изменился адрес поставщика. Если от него было несколько поставок, то придется менять несколько записей.
Аномалия удаления: при удалении в архив записей обо всех поставках определённого поставщика все данные об этом поставщике (название, адрес) будут утеряны.
Аномалия добавления: нельзя добавить сведения о поставщике, пока от него нет ни одной поставки.
Для решения проблемы аномалии модификации данных при проектировании РБД проводится нормализация отношений.

Нормализация схемы отношения
Нормализация схемы отношения выполняется путём декомпозиции схемы.
Декомпозицией схемы отношения R называется замена её совокупностью схем отношений Аi таких, что
и не требуется, чтобы отношения Аi были непересекающимися. Декомпозиция отношения не должна приводить к потере зависимостей между атрибутами сущностей. Для декомпозиции должна существовать операция реляционной алгебры, применение которой позволит восстановить исходное отношение.
Покажем нормализацию на примере отношения КНИГИ :
Id – идентификатор (первичный ключ),
Code – шифр рубрики (по ББК – библиотечно-библиографической классификации),
Theme – название рубрики (по ББК),
Title – название книги,
Author – автор(ы),
Editor – редактор(ы),
Type – тип издания (учебник, учебное пособие, сборник и.т.п.),
Year – год издания,
Pg – количество страниц.

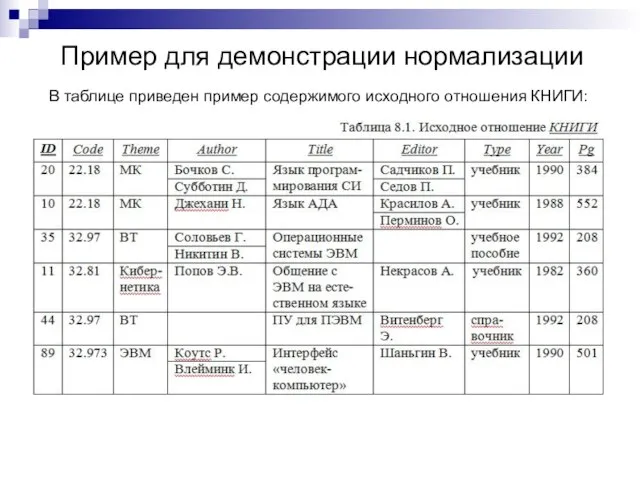
Пример для демонстрации нормализации
В таблице приведен пример содержимого исходного отношения КНИГИ:

Первая нормальная форма
Введём понятие простого и сложного атрибута:
Простой атрибут – это атрибут, значения которого атомарны (т.е. неделимы).
Сложный атрибут может иметь значение, представляющее собой конкатенацию нескольких значений одного или разных доменов. Аналогом сложного атрибута может быть агрегат или повторяющийся агрегат данных.
Первая нормальная форма (1НФ).
Отношение приведено к 1НФ, если все его атрибуты простые.

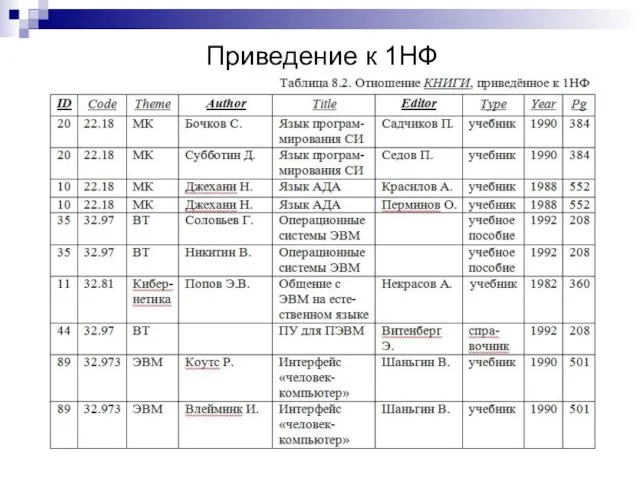
Приведение к 1НФ

Вторая нормальная форма
Введём понятие функциональной зависимости. Пусть X и Y – атрибуты (группы атрибутов) некоторого отношения. Говорят, что Y функционально зависит от X, если в любой момент времени каждому значению X=х соответствует единственное значение Y=y (X→Y). (При этом любому значению Y=y может соответствовать несколько значений Х=(х1, х2,…)).
Атрибут X в функциональной зависимости X→Y называется детерминантом отношения.
Неключевой атрибут функционально полно зависит от составного ключа, если он функционально зависит от ключа, но не находится в функциональной зависимости ни от какой части составного ключа.
Вторая нормальная форма (2НФ).
Отношение находится во 2НФ, если оно приведено к 1НФ и каждый неключевой атрибут функционально полно зависит от составного ключа.
Для того чтобы привести отношение ко 2НФ, нужно:
построить его проекцию, исключив атрибуты, которые не находятся в функционально полной зависимости от составного ключа;
построить дополнительные проекции на часть составного ключа и атрибуты, функционально зависящие от этой части ключа.

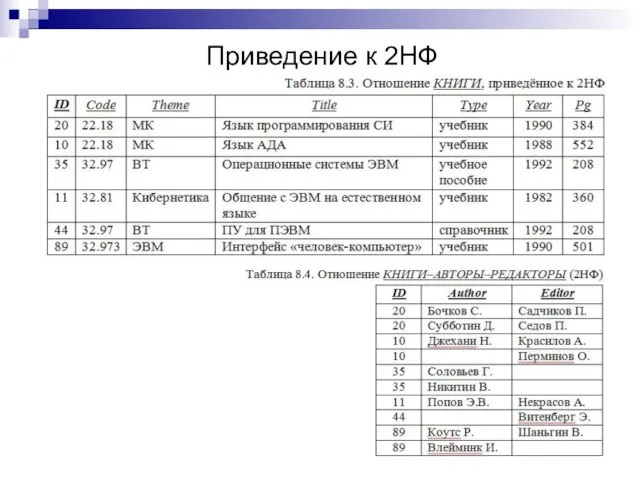
Приведение к 2НФ

Третья нормальная форма
Рассмотрим понятие транзитивной зависимости.
Пусть X, Y, Z – атрибуты некоторого отношения. При этом X→Y и Y→Z, но обратное соответствие отсутствует, т.е. Z не зависит от Y или Y не зависит от X. Тогда говорят, что Z транзитивно зависит от X (X→→Z).
Третья нормальная форма (3НФ).
Отношение находится в 3НФ, если оно находится во 2НФ и в нем отсутствуют транзитивные зависимости.
Исключение:
если для атрибутов X,Y,Z есть транзитивная зависимость X →→ Z, и при этом Y → X или Z → Y, то такая зависимость не требует декомпозиции отношения.
Например, для отношения АВТОМОБИЛИ с первичным ключом Государственный номерной знак и полями № кузова и № двигателя очевидно, что номера кузова и двигателя зависят как друг от друга, так и от первичного ключа. Но эта зависимость взаимно однозначная, поэтому декомпозиция отношения не нужна.

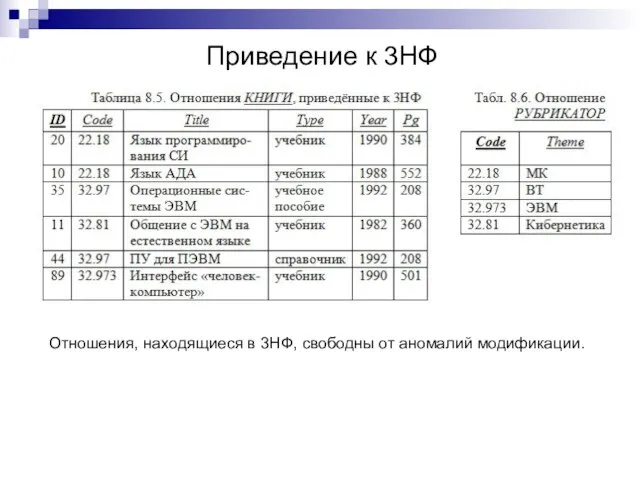
Приведение к 3НФ
Отношения, находящиеся в 3НФ, свободны от аномалий модификации.

Четвертая нормальная форма
Введём понятие многозначной зависимости.
Многозначная зависимость существует, если заданным значениям атрибута X соответствует множество, состоящее из нуля (или более) значений атрибута Y. Если в отношении есть многозначные зависимости, то схема отношения должна находиться в 4НФ.
Различают тривиальные и нетривиальные многозначные зависимости. Тривиальной называется многозначная зависимость X–»Y, для которой Y ⊂ X или X U Y = R, где R – рассматриваемое отношение.
Тривиальная многозначная зависимость не нарушает 4НФ. Если хотя бы одно из двух этих условий не выполняется (т.е. Y не является подмножеством X или X U Y состоит не из всех атрибутов R), то такая многозначная зависимость называется нетривиальной.
Четвертая нормальная форма (4НФ).
Отношение находится в 4НФ, если оно находится в 3НФ и в нем отсутствуют нетривиальные многозначные зависимости.

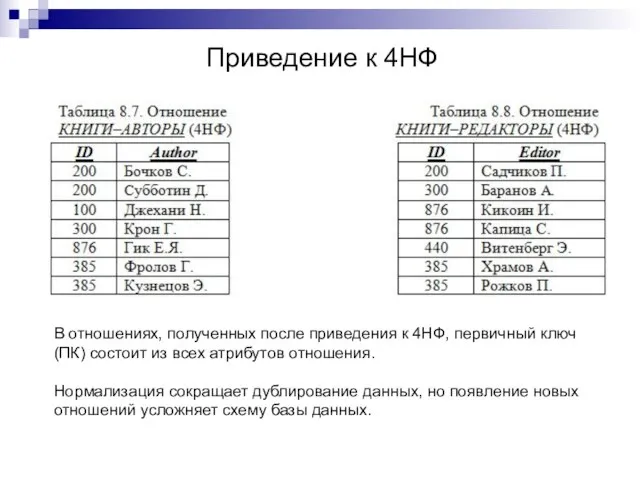
Приведение к 4НФ
В отношениях, полученных после приведения к 4НФ, первичный ключ (ПК) состоит из всех атрибутов отношения.
Нормализация сокращает дублирование данных, но появление новых отношений усложняет схему базы данных.

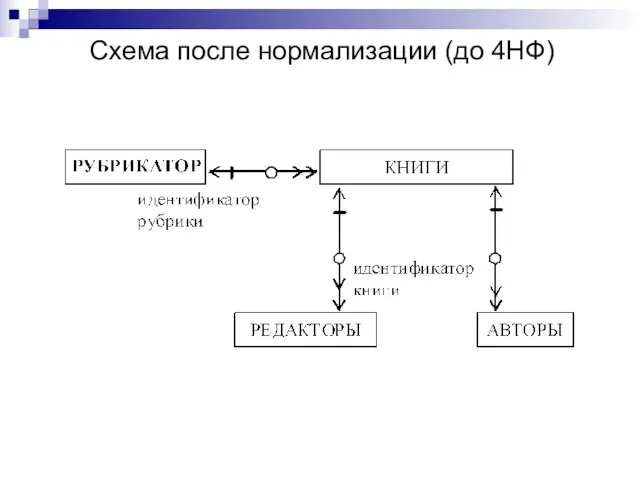
Схема после нормализации (до 4НФ)

Усиленная 3НФ
Нормальная форма Бойса-Кодда (НФБК):
Все детерминанты отношения должны быть его
потенциальными ключами.
Покажем нарушение НФБК на примере отношения "Переговоры" (Interview):
IdClient – номер клиента,
IdStaff – номер сотрудника,
Room – номер комнаты для переговоров,
Vdate – дата встречи,
Vtime – время встречи.

Анализ на соответствие НФБК
Данные в этой таблице должны удовлетворять следующим правилам:
С каждым клиентом в день происходит не более одной встречи.
В каждый момент времени в одной комнате происходит только одна встреча.
Каждый сотрудник встречается с клиентом один на один.
На один день сотруднику выделяется одна комната для переговоров.
В соответствие с правилами в отношении "Работа с клиентами" (Interview) есть 4 детерминанта:
fd1: IdClient, Vdate –> IdStaff, Room, Vtime.
fd2: Room, Vdate, Vtime –> IdStaff, IdClient.
fd3: IdStaff, Vdate, Vtime –> IdClient, Room.
fd4: IdStaff, Vdate –> Room.
Вопрос: все ли детерминанты являются потенциальными ключами?
Первые три являются потенциальными ключами, а fd4 – нет. Это может привести к аномалии обновления данных при смене номера комнаты.

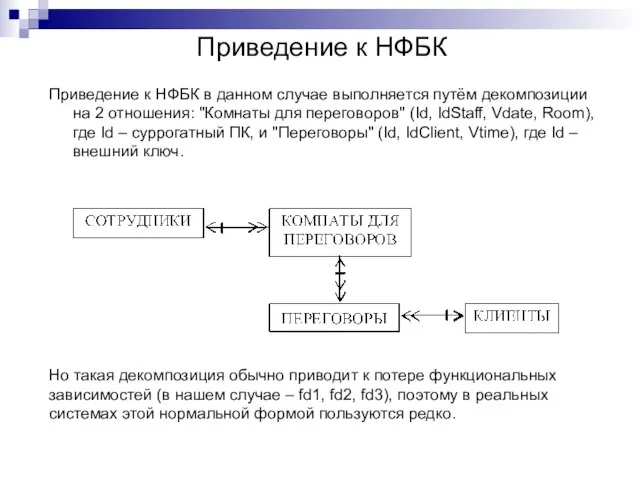
Приведение к НФБК
Приведение к НФБК в данном случае выполняется путём декомпозиции на 2 отношения: "Комнаты для переговоров" (Id, IdStaff, Vdate, Room), где Id – суррогатный ПК, и "Переговоры" (Id, IdClient, Vtime), где Id – внешний ключ.
Но такая декомпозиция обычно приводит к потере функциональных зависимостей (в нашем случае – fd1, fd2, fd3), поэтому в реальных системах этой нормальной формой пользуются редко.

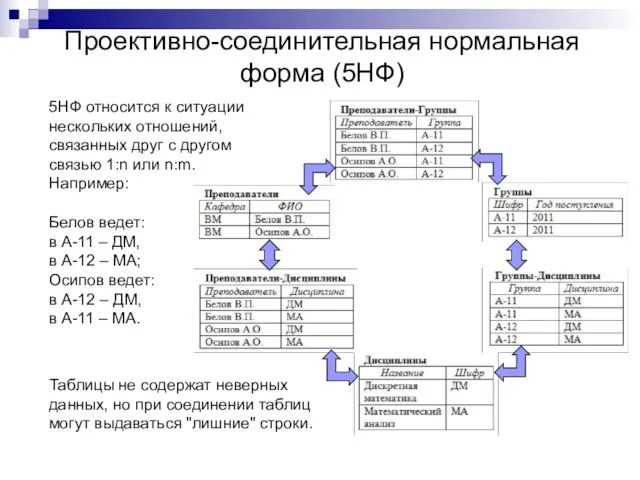
Проективно-соединительная нормальная форма (5НФ)
5НФ относится к ситуации нескольких отношений, связанных друг с другом связью 1:n или n:m.
Например:
Таблицы не содержат неверных данных, но при соединении таблиц могут выдаваться "лишние" строки.
Белов ведет: в А-11 – ДМ,
в А-12 – МА; Осипов ведет: в А-12 – ДМ, в А-11 – МА.

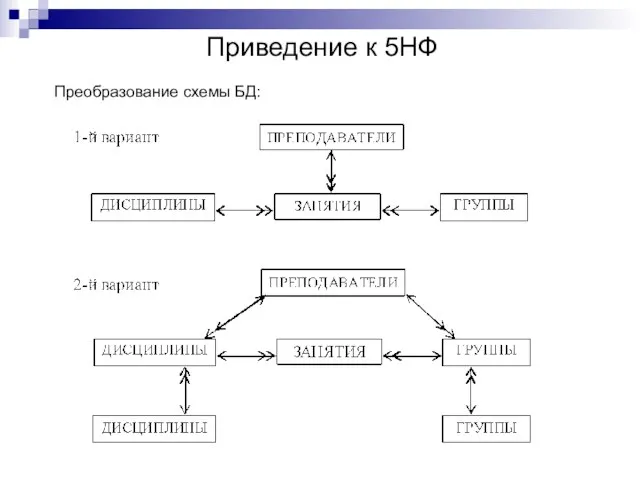
Приведение к 5НФ
Преобразование схемы БД: