О новых способах увеличения информационной емкости волоконно-оптических линий связи

Передача данных по одному волоконному световоду на различных частотах
Дальнейшее увеличение информационной ёмкости (BL, где В – пропускная способность линии,L – дальность передачи) возможно на основе объединения технологий:
Информационная ёмкость
б) Спектральное уплотнение:
а)Дисперсионное управление:
- период
- средняя дисперсия
Пропускная способность:
- скорость передачи в одном канале
- число каналов
Каналы (№): 1 2 3 4 5 6 7 8

Две основные задачи:
Изучение фундаментальных свойств оптических импульсов (дисперсионно - управляемых солитонов) в системах с периодически меняющимися коэффициентами дисперсии и нелинейности.
Оптимизация конкретных конфигураций волоконно-оптический линий связи с целью увеличения информационной ёмкости.

Математическая модель: A
Обобщенное нелинейное уравнение Шредингера (ОНУШ):
Дисперсионный параметр:
- эффективный коэффициент нелинейности.
Основная математическая модель для описания эволюции оптических импульсов в волоконных световодах:
- медленная комплексная огибающая электромагнитного поля

Математическая модель: A
И формально решение выглядит так:
- оператор линейной части,
- нелинейный оператор, тогда
Численный алгоритм реализации ОНУШ :
Метод Фурье расщепления по физическим процессам

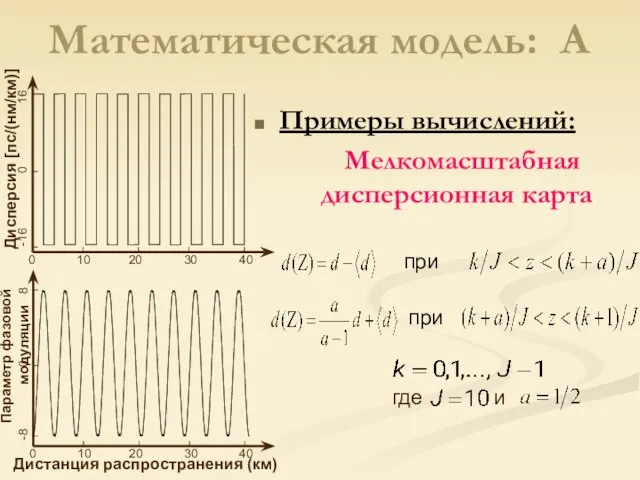
Математическая модель: A
Примеры вычислений:
Мелкомасштабная дисперсионная карта
где и
при
Дистанция распространения (км)
Параметр фазовой
0 10 20 30 40
при
модуляции

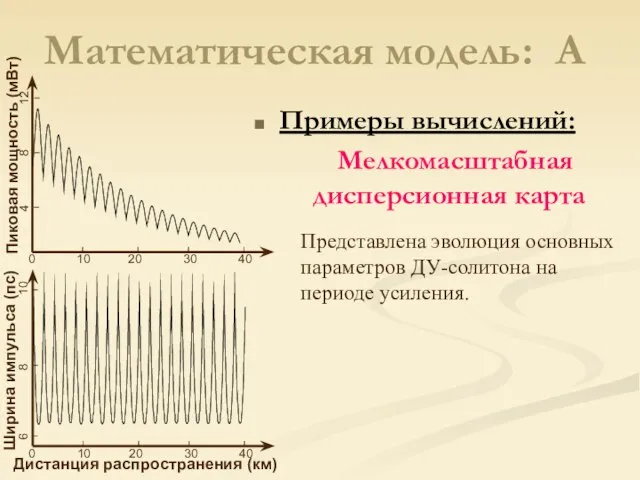
Математическая модель: A
Примеры вычислений:
Мелкомасштабная дисперсионная карта
Представлена эволюция основных параметров ДУ-солитона на периоде усиления.

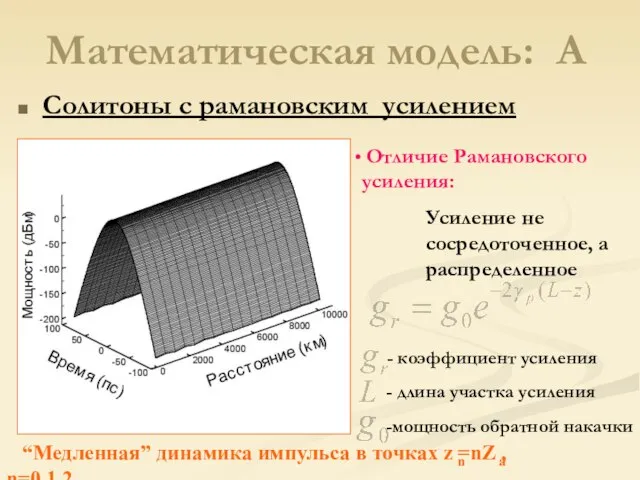
Математическая модель: A
Солитоны с рамановским усилением
Отличие Рамановского усиления:
Усиление не сосредоточенное, а распределенное
“Медленная” динамика импульса в точках z =nZ , n=0,1,2…
- длина участка усиления
мощность обратной накачки
n
a
- коэффициент усиления

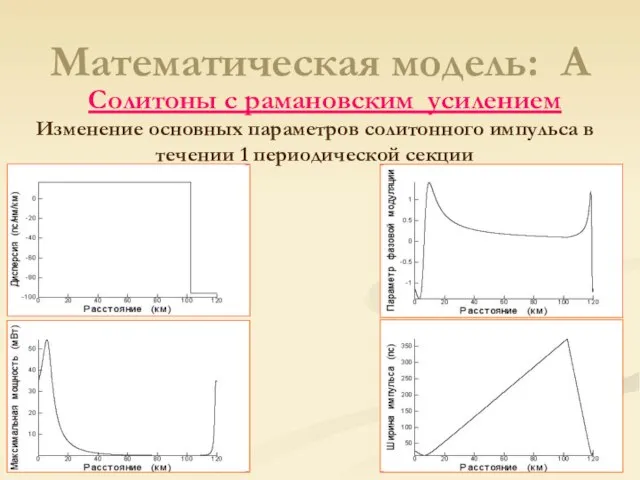
Солитоны с рамановским усилением
Математическая модель: A
Изменение основных параметров солитонного импульса в течении 1 периодической секции

Математическая модель: Б
Усредненное (path-averaged) уравнение спектральной области
, где
и
В предположении, что , где дисперсионная длина, нелинейная длина, имеет место
- усредненная комплексная огибающая в спектральной области
-ядро интегрального оператора, определяющее тип ВОЛС

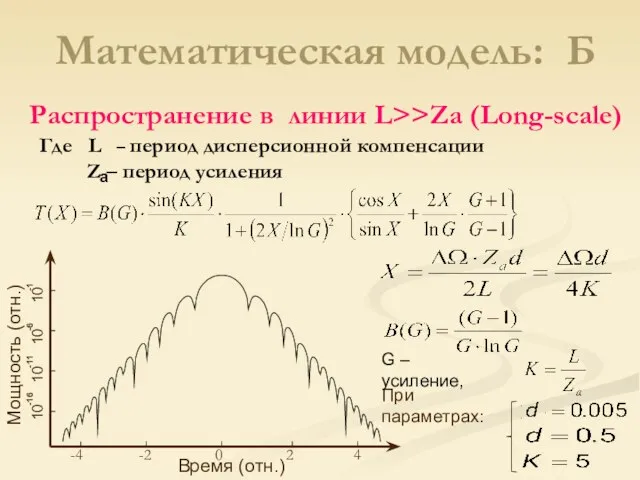
Математическая модель: Б
Распространение в линии L>>Za (Long-scale)
При параметрах:
-4 -2 0 2 4
Время (отн.)
Мощность (отн.)
G – усиление,
Где L – период дисперсионной компенсации
Z – период усиления
a

Математическая модель: Б
Распространение в линии L<
Где
При параметрах

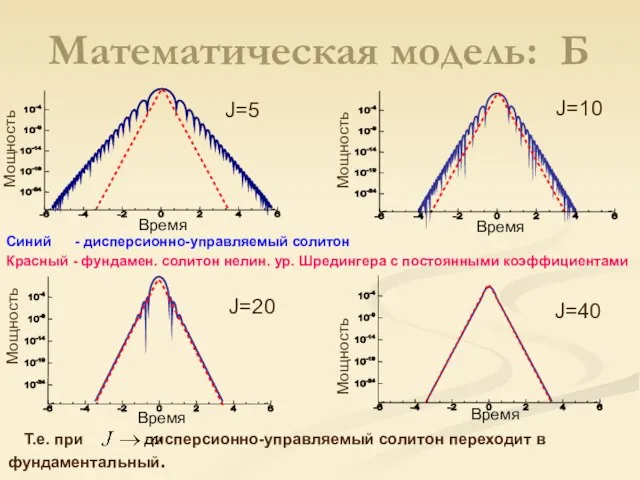
Время
J=5
Мощность
J=10
Время
Мощность
Синий - дисперсионно-управляемый солитон
Красный - фундамен. солитон нелин. ур. Шредингера с постоянными коэффициентами
Математическая модель: Б
Время
Мощность
J=20
J=40
Мощность
Время
Т.е. при дисперсионно-управляемый солитон переходит в фундаментальный.

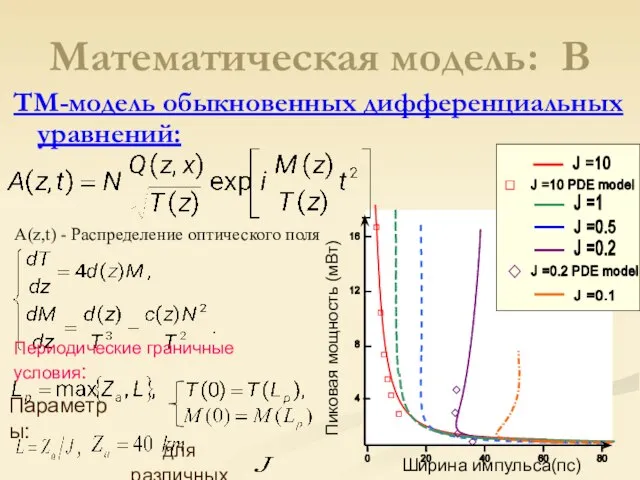
Математическая модель: В
TM-модель обыкновенных дифференциальных уравнений:
Периодические граничные условия:
Параметры:
для различных
Ширина импульса(пс)
Пиковая мощность (мВт)
A(z,t) - Распределение оптического поля

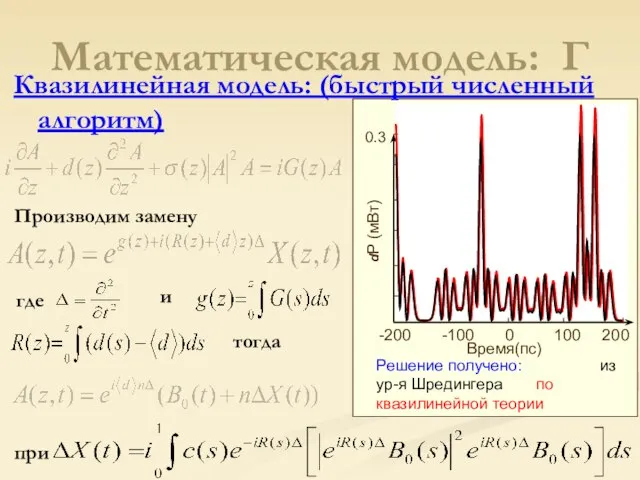
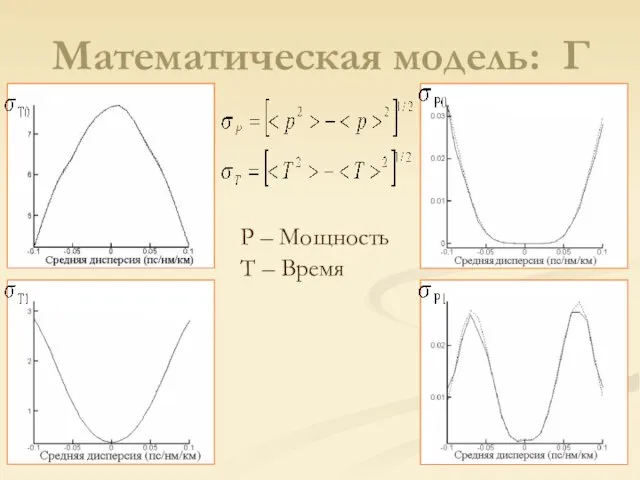
Математическая модель: Г
Квазилинейная модель: (быстрый численный алгоритм)
Производим замену
где
тогда
при
и

P – Мощность
T – Время
Математическая модель: Г

Проблемы оптимизации
Главная задача – увеличение битовой скорости и дистанции распространения
Критерием качества для цифровых приемников является частота появления ошибочных битов (BER).
Современный стандарт:
1 ошибочный бит на приемнике на 10 переданных битов
В предположении гауссовой статистики, где
мат. ожидание 0 и 1;
соответствующая дисперсия (средне-квадратичные отклонения)
9

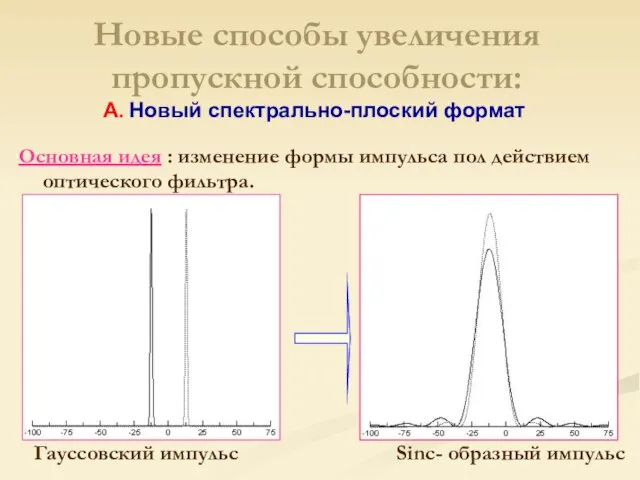
Новые способы увеличения пропускной способности:
Основная идея : изменение формы импульса пол действием оптического фильтра.
Гауссовский импульс
Sinc- образный импульс
А. Новый спектрально-плоский формат

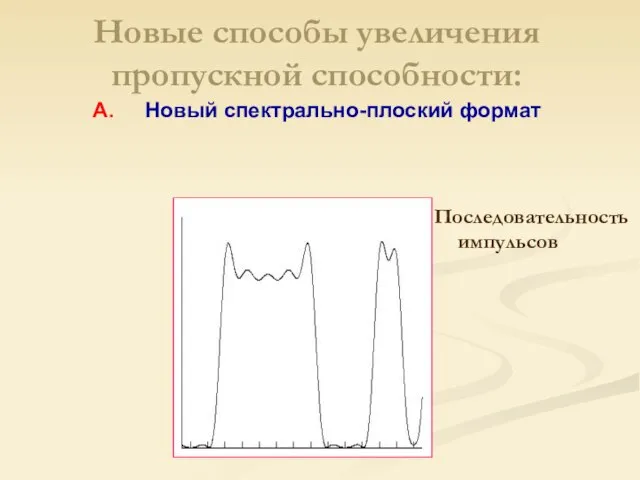
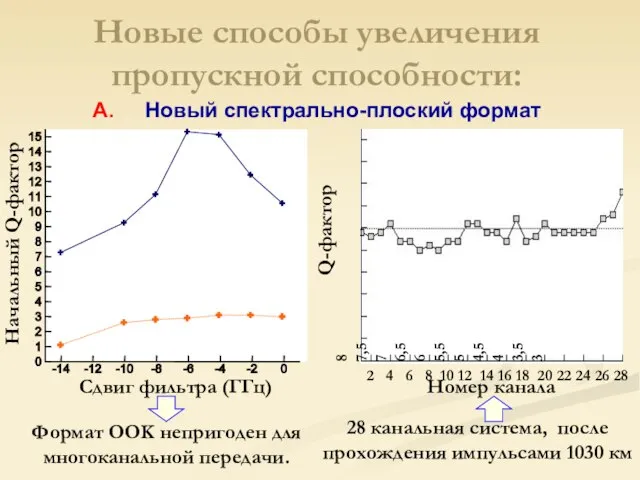
Последовательность импульсов
Новые способы увеличения пропускной способности:
А. Новый спектрально-плоский формат

Формат OOK непригоден для многоканальной передачи.
28 канальная система, после прохождения импульсами 1030 км
Сдвиг фильтра (ГГц)
Начальный Q-фактор
Новые способы увеличения пропускной способности:
А. Новый спектрально-плоский формат
Номер канала
2 4 6 8 10 12 14 16 18 20 22 24 26 28
Q-фактор
8
7,5
7
6,5
6
5,5
5
4,5
4
3,5
3

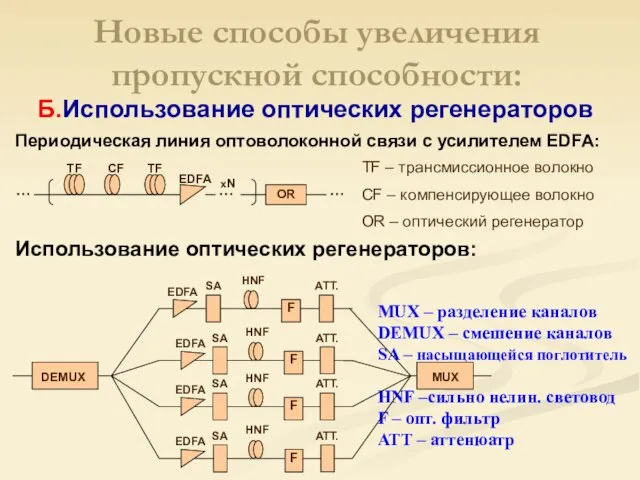
MUX – разделение каналов
DEMUX – смешение каналов
SA – насыщающейся поглотитель
HNF –сильно нелин. световод
F – опт. фильтр
ATT – аттенюатр
Периодическая линия оптоволоконной связи с усилителем EDFA:
Использование оптических регенераторов:
TF – трансмиссионное волокно
CF – компенсирующее волокно
OR – оптический регенератор
Б. Использование оптических регенераторов
Новые способы увеличения пропускной способности:

Мощность импульса на выходе: (Т – передаточная функция)
Входной сигнал запускается в оптический регенератор:
- усиливается усилителем EDFA
- насыщается в поглотителе
Функция потерь
в насыщающемся поглотителе:
Где
- распределение мощности сигнала
- постоянные потери
- пороговая мощность насыщения
- время спада импульса
Б. Использование оптических регенераторов
Новые способы увеличения пропускной способности:

Оптимизации симметричной линий связи TL(20км)+RTL(20км)+TL(20км)+EDFA Изолинии пройденного расстояния в плоскостях параметров:
В аналогичной системе без регенераторов – дистанции менее 2000км
Б. Использование оптических регенераторов
Новые способы увеличения пропускной способности:

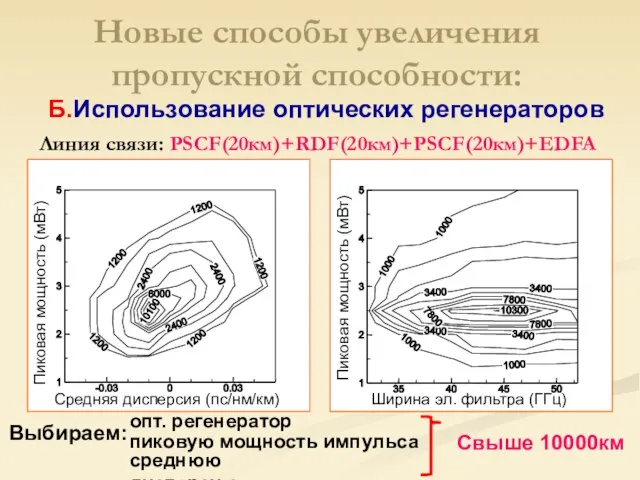
Линия связи: PSCF(20км)+RDF(20км)+PSCF(20км)+EDFA
Выбираем:
опт. регенератор
пиковую мощность импульса
среднюю дисперсию
Свыше 10000км
Б. Использование оптических регенераторов
Новые способы увеличения пропускной способности:

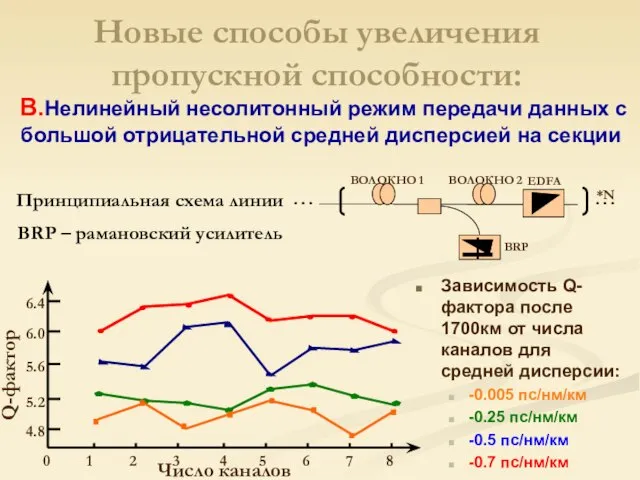
Зависимость Q-фактора после 1700км от числа каналов для средней дисперсии:
-0.005 пс/нм/км
-0.25 пс/нм/км
-0.5 пс/нм/км
-0.7 пс/нм/км
В.Нелинейный несолитонный режим передачи данных с большой отрицательной средней дисперсией на секции
Новые способы увеличения пропускной способности:
Принципиальная схема линии
BRP – рамановский усилитель

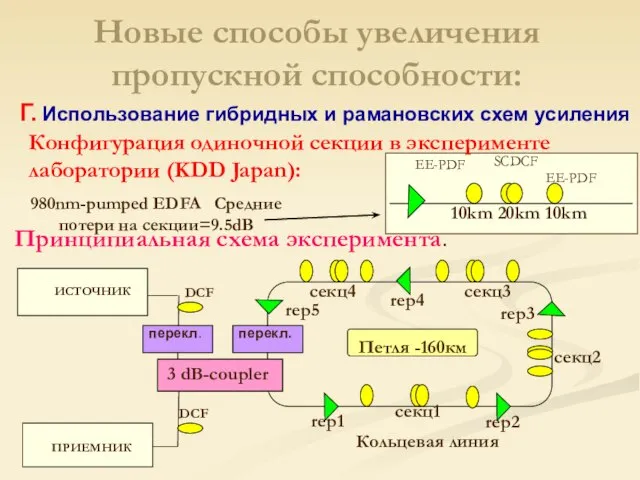
Конфигурация одиночной секции в эксперименте лаборатории (KDD Japan):
EE-PDF
EE-PDF
SCDCF
10km 20km 10km
980nm-pumped EDFA Средние потери на секции=9.5dB
Г. Использование гибридных и рамановских схем усиления
Новые способы увеличения пропускной способности:
ПРИЕМНИК
ИСТОЧНИК
3 dB-coupler
Кольцевая линия
перекл.
DCF
rep1
rep2
rep3
rep4
rep5
секц1
секц2
секц4
секц3
Петля -160км
перекл.
DCF
Принципиальная схема эксперимента.

Число каналов
0 1 2 3 4 5 6 7 8
16
14
12
10
Q (dB)
2
Численное моделирование
Сравнение численных экспериментов и результатов моделирования (Система многоканальной передачи)
Экспериментальные данные
Новые способы увеличения пропускной способности:
Г. Использование гибридных и рамановских схем усиления

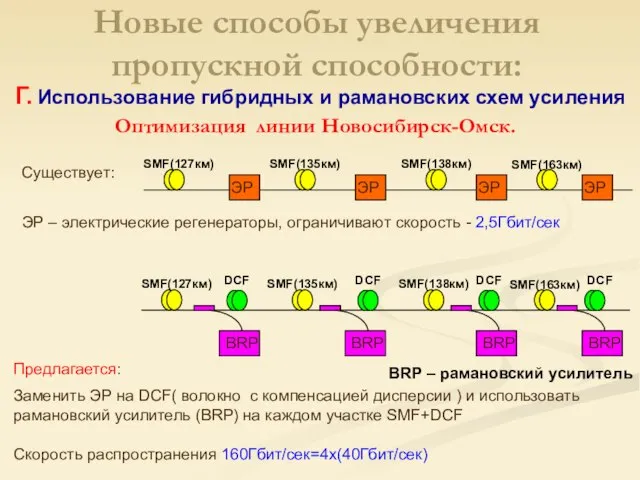
Оптимизация линии Новосибирск-Омск.
Предлагается:
Заменить ЭР на DCF( волокно с компенсацией дисперсии ) и использовать рамановский усилитель (BRP) на каждом участке SMF+DCF
Новые способы увеличения пропускной способности:
Г. Использование гибридных и рамановских схем усиления
Существует:
ЭР – электрические регенераторы, ограничивают скорость - 2,5Гбит/сек
Скорость распространения 160Гбит/сек=4х(40Гбит/сек)
SMF(127км)
SMF(135км)
SMF(138км)
SMF(163км)
DCF
DCF
DCF
DCF
BRP – рамановский усилитель

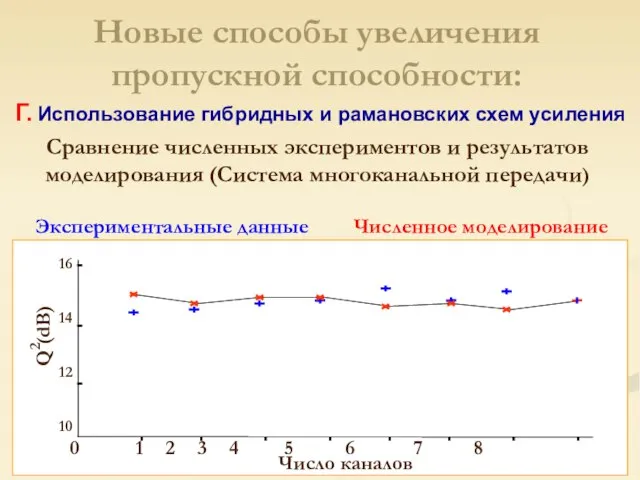
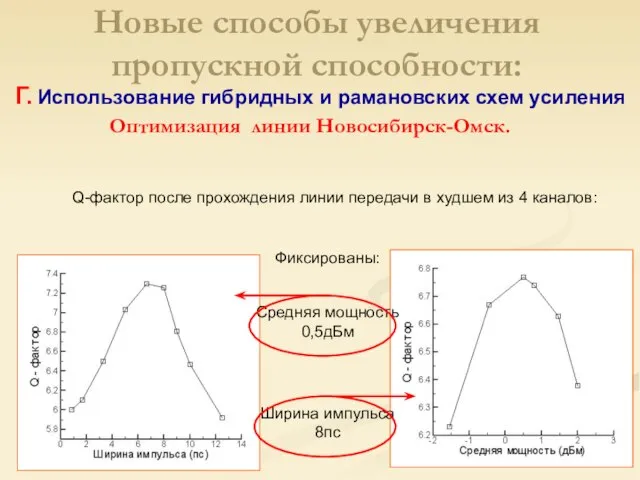
Оптимизация линии Новосибирск-Омск.
Новые способы увеличения пропускной способности:
Г. Использование гибридных и рамановских схем усиления
Q-фактор после прохождения линии передачи в худшем из 4 каналов:
Фиксированы:
Средняя мощность 0,5дБм
Ширина импульса 8пс