Обобщающий урок

План урока
Презентация учащихся (домашнее задание)
Устная работа
Составь задачу
Самостоятельная работа

Вы хотите:
Начать презентацию снова;
Закончить работу.

Заключение
На этом наш урок закончен
Спасибо за работу

1. Вспомните определение сферы, шара.

2. Сколько плоскостей можно провести через 2 точки поверхности сферы?
через 3 точки?

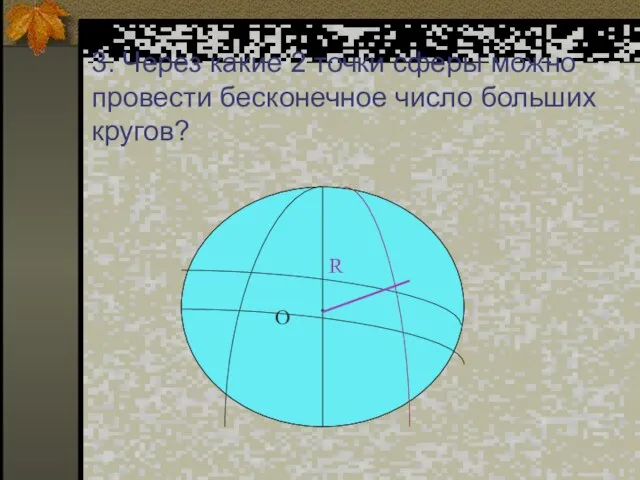
3. Через какие 2 точки сферы можно провести бесконечное число больших кругов?

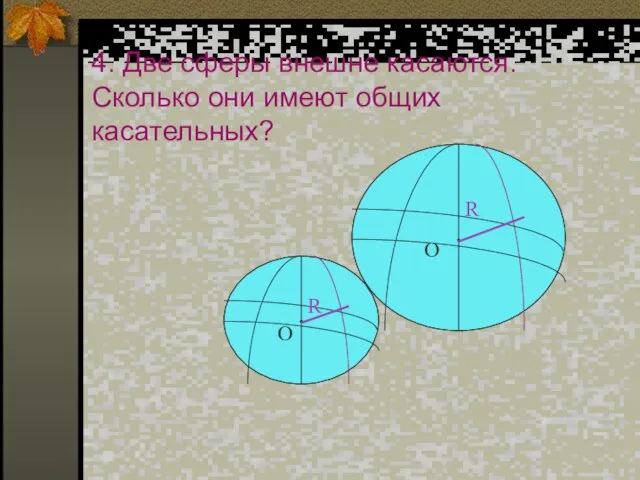
4. Две сферы внешне касаются. Сколько они имеют общих касательных?

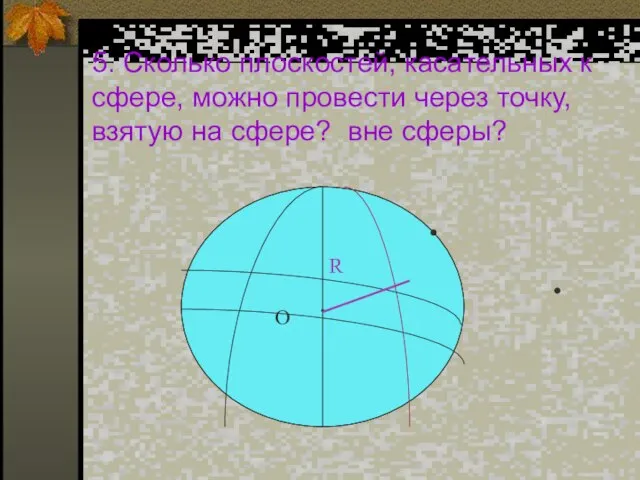
5. Сколько плоскостей, касательных к сфере, можно провести через точку, взятую на сфере? вне сферы?

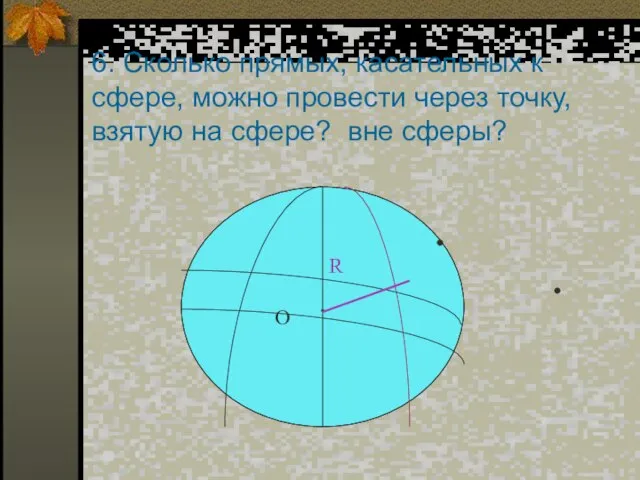
6. Сколько прямых, касательных к сфере, можно провести через точку, взятую на сфере? вне сферы?

7. Вращением какой геометрической фигуры можно получить сферу, шар?

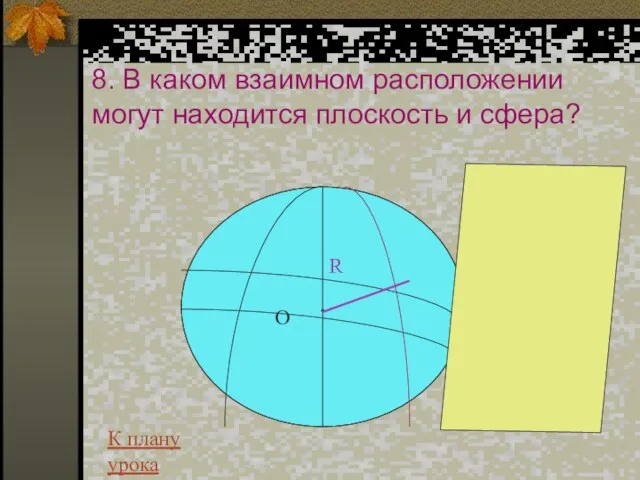
8. В каком взаимном расположении могут находится плоскость и сфера?
К плану урока

К плану урока

Составьте всевозможные задачи по данному чертежу.
Дано:
Сфера R= 5 см
т.О(-4; 6; 2)
Секущая плоскость на расстоянии d = 3 см от центра.
1. Уравнение сферы.
Найти:
2.Радиус и площадь круга, получен-ного в сечении.
3. Площадь сферы.
Решение:
(х+4)2+(у-6)2+ +(z-2)2=25
r = 4 см
Sсеч = 16π см2
Sсф = 4π 52= =100π см2
К плану урока

К плану урока

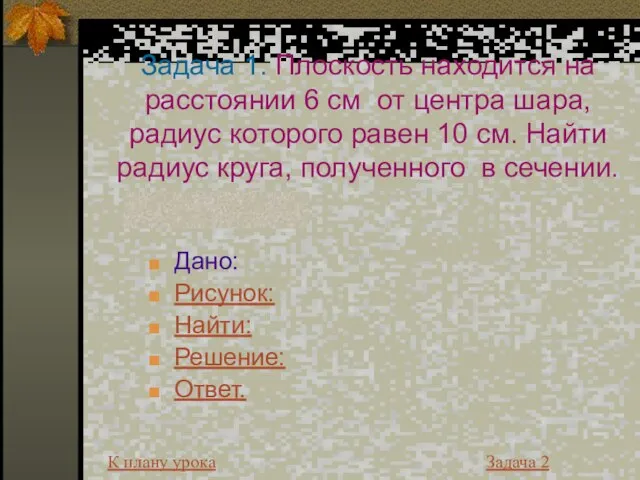
Задача 1. Плоскость находится на расстоянии 6 см от центра шара, радиус которого равен 10 см. Найти радиус круга, полученного в сечении.
Дано:
Рисунок:
Найти:
Решение:
Ответ.
К плану урока
Задача 2
Помочь?

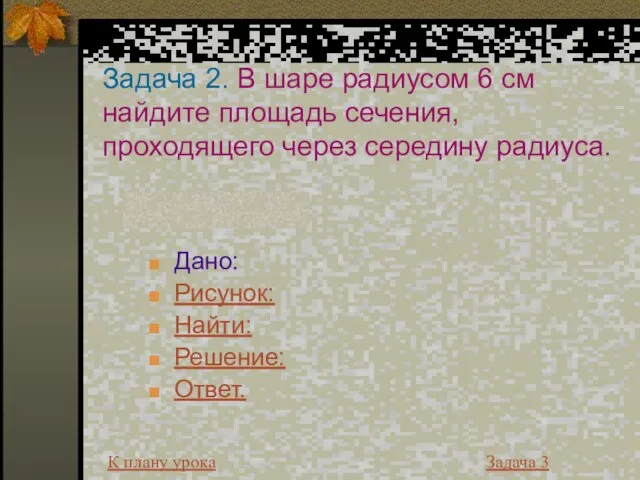
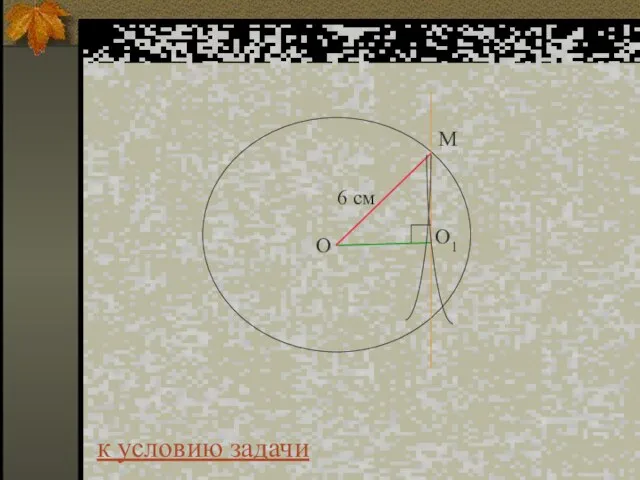
Задача 2. В шаре радиусом 6 см найдите площадь сечения, проходящего через середину радиуса.
Дано:
Рисунок:
Найти:
Решение:
Ответ.
К плану урока
Задача 3
Помочь?

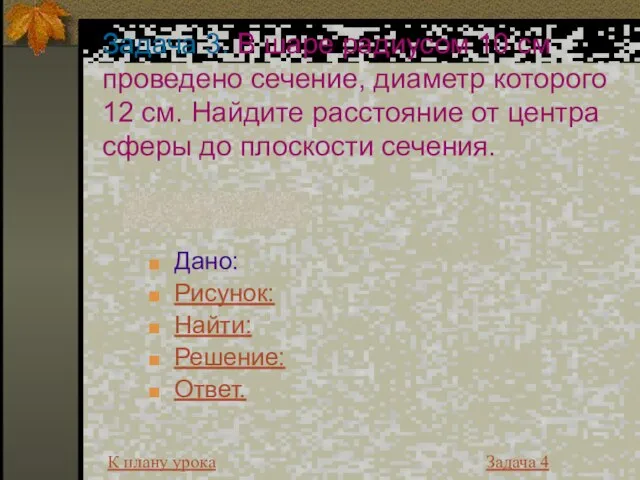
Задача 3. В шаре радиусом 10 см проведено сечение, диаметр которого 12 см. Найдите расстояние от центра сферы до плоскости сечения.
Дано:
Рисунок:
Найти:
Решение:
Ответ.
К плану урока
Задача 4
Помочь?

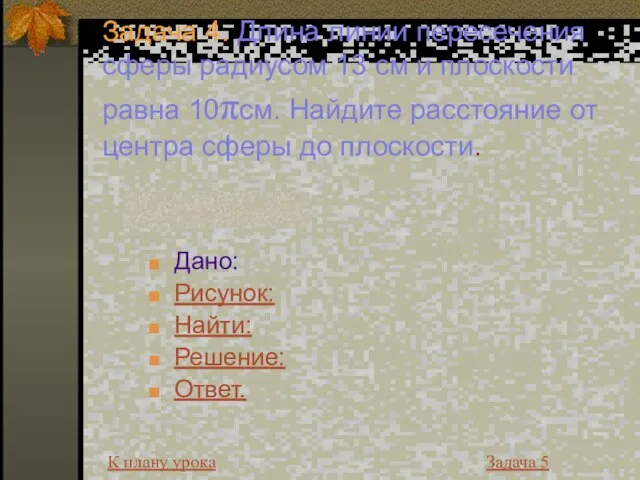
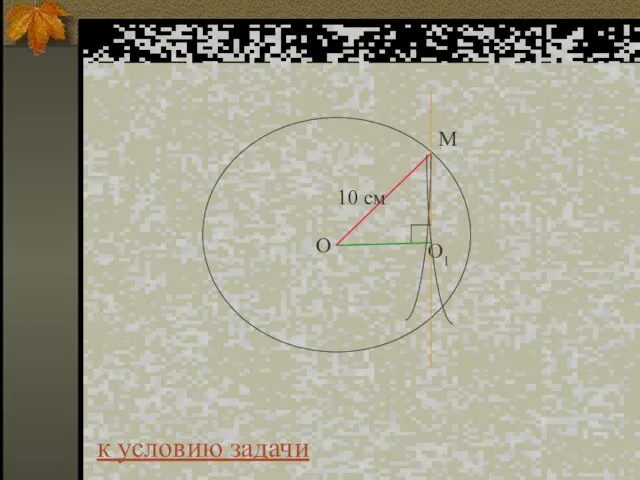
Задача 4. Длина линии пересечения сферы радиусом 13 см и плоскости равна 10πсм. Найдите расстояние от центра сферы до плоскости.
Дано:
Рисунок:
Найти:
Решение:
Ответ.
К плану урока
Задача 5
Помочь?

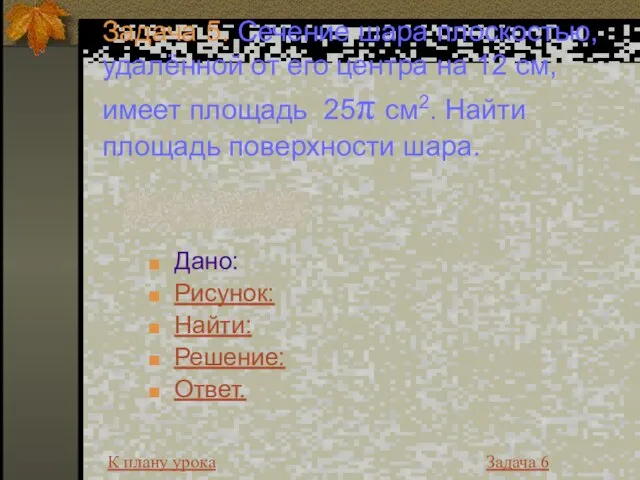
Задача 5. Сечение шара плоскостью, удалённой от его центра на 12 см, имеет площадь 25π см2. Найти площадь поверхности шара.
Дано:
Рисунок:
Найти:
Решение:
Ответ.
К плану урока
Задача 6
Помочь?

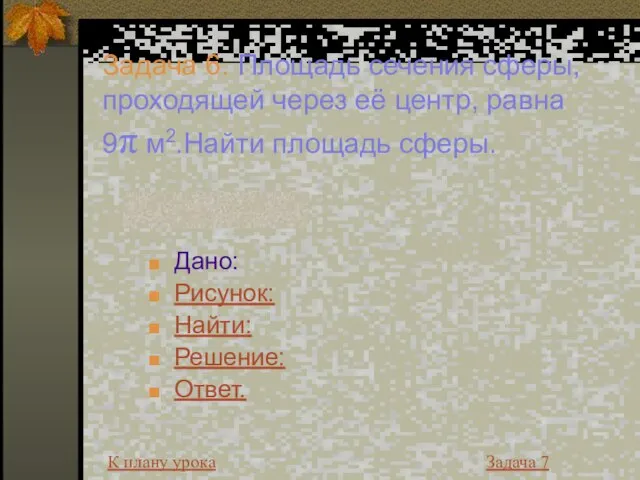
Задача 6. Площадь сечения сферы, проходящей через её центр, равна 9π м2.Найти площадь сферы.
Дано:
Рисунок:
Найти:
Решение:
Ответ.
К плану урока
Задача 7
Помочь?

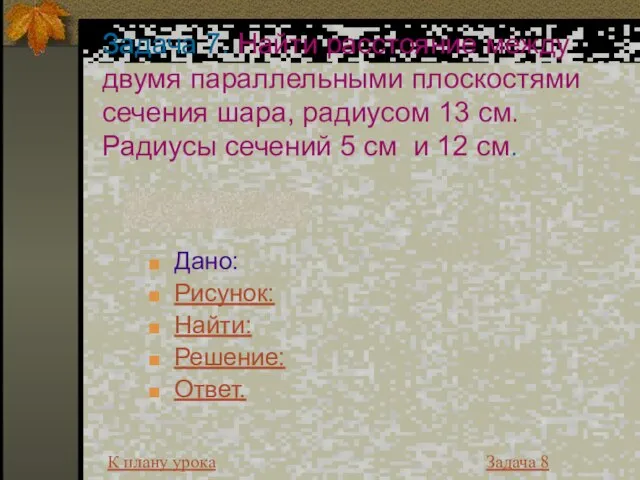
Задача 7. Найти расстояние между двумя параллельными плоскостями сечения шара, радиусом 13 см. Радиусы сечений 5 см и 12 см.
Дано:
Рисунок:
Найти:
Решение:
Ответ.
К плану урока
Задача 8
Помочь?

Задача 8. Вершины прямоугольного треугольника АВС лежат на шаровой поверхности, радиус которой 13 см. Найти расстояние от центра шара до плоскости АВС, если АВ = 6 см, ВС = 8 см, угол В = 900.
Дано:
Рисунок:
Найти:
Решение:
Ответ.
К плану урока
Задача 9
Помочь?

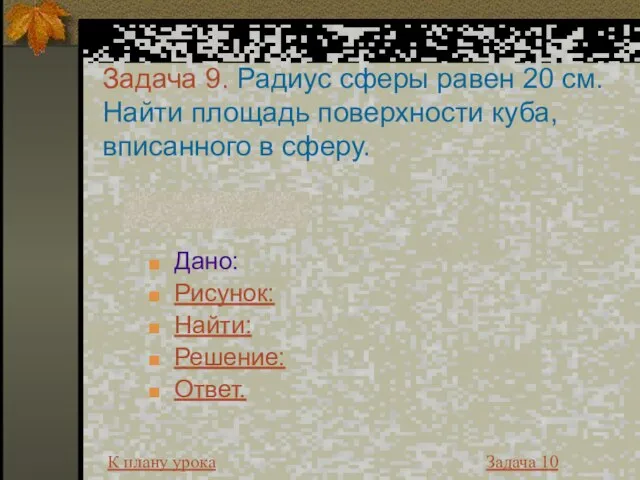
Задача 9. Радиус сферы равен 20 см. Найти площадь поверхности куба, вписанного в сферу.
Дано:
Рисунок:
Найти:
Решение:
Ответ.
К плану урока
Задача 10
Помочь?

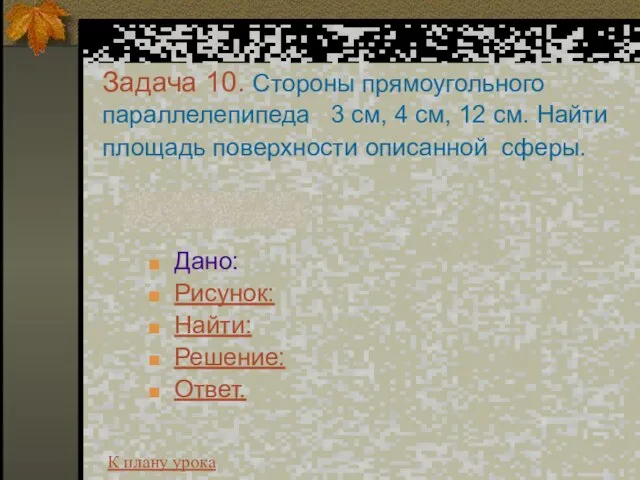
Задача 10. Стороны прямоугольного параллелепипеда 3 см, 4 см, 12 см. Найти площадь поверхности описанной сферы.
Дано:
Рисунок:
Найти:
Решение:
Ответ.
К плану урока
Помочь?

К плану урока

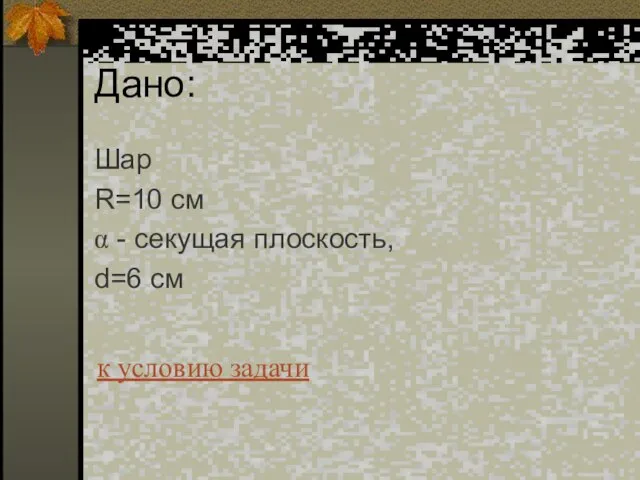
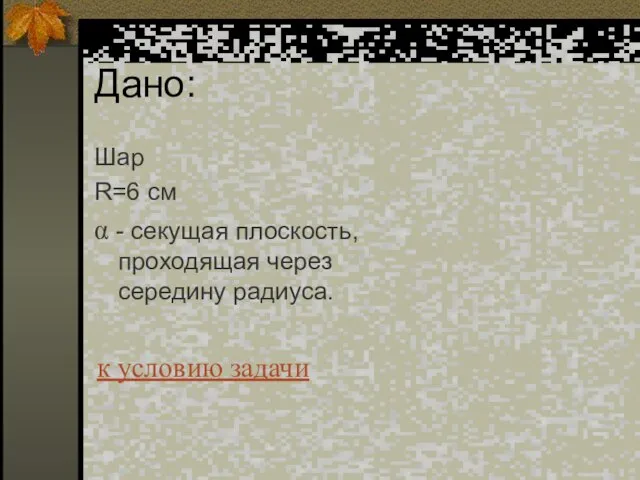
Дано:
Шар
R=10 см
α - секущая плоскость,
d=6 cм
к условию задачи

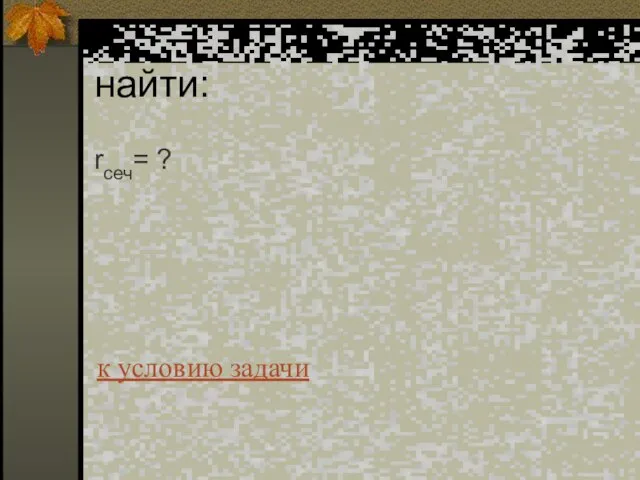
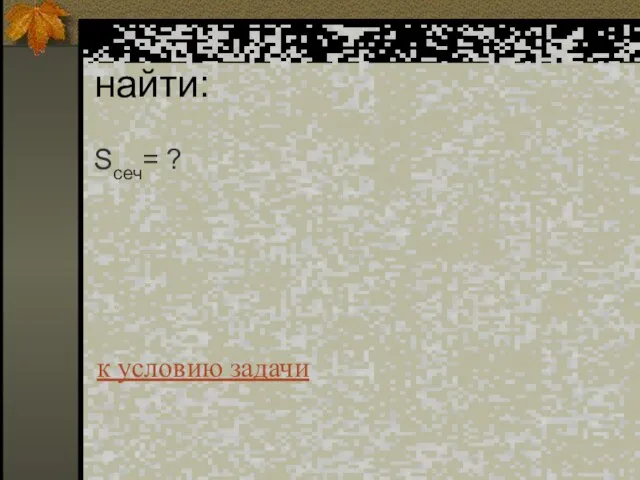
найти:
rсеч= ?
к условию задачи

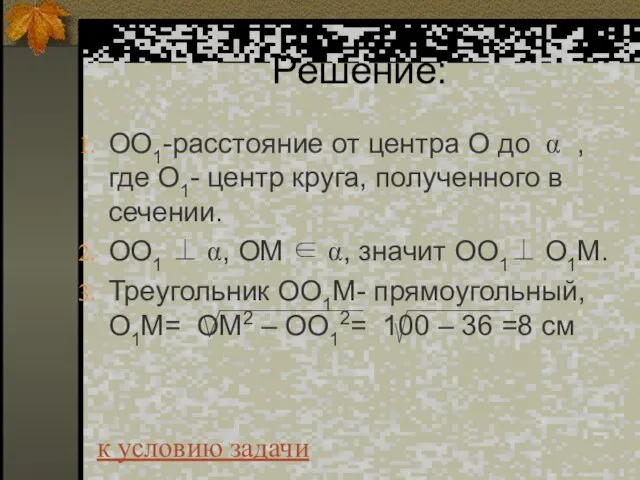
Решение:
ОО1-расстояние от центра О до α , где О1- центр круга, полученного в сечении.
ОО1 ⊥ α, ОМ ∈ α, значит ОО1⊥ О1М.
Треугольник ОО1М- прямоугольный, О1М= ОМ2 – ОО12= 100 – 36 =8 см
к условию задачи

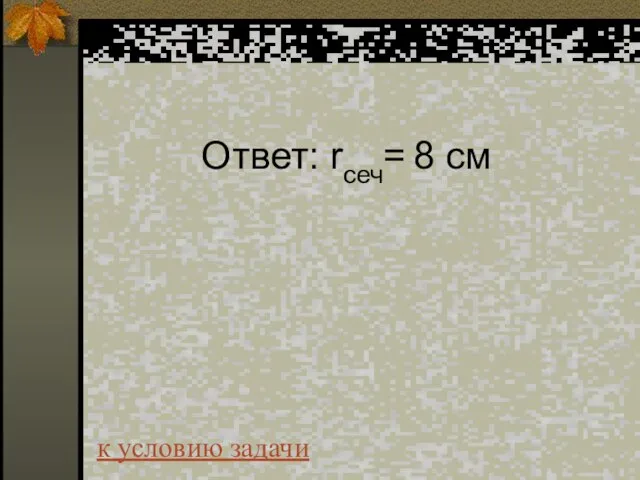
Ответ: rсеч= 8 см
к условию задачи

к условию задачи
М
О1
О
10 см
6 см

Дано:
Шар
R=6 см
α - секущая плоскость, проходящая через середину радиуса.
к условию задачи

найти:
Sсеч= ?
к условию задачи

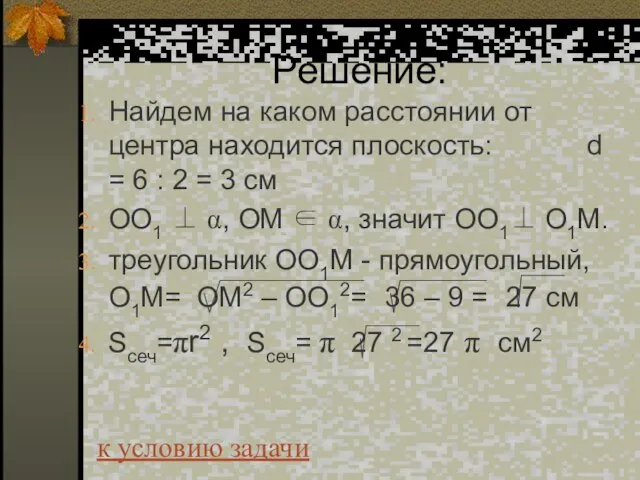
Решение:
Найдем на каком расстоянии от центра находится плоскость: d = 6 : 2 = 3 см
ОО1 ⊥ α, ОМ ∈ α, значит ОО1⊥ О1М.
треугольник ОО1М - прямоугольный, О1М= ОМ2 – ОО12= 36 – 9 = 27 см
Sсеч=πr2 , Sсеч= π 27 2 =27 π см2
к условию задачи

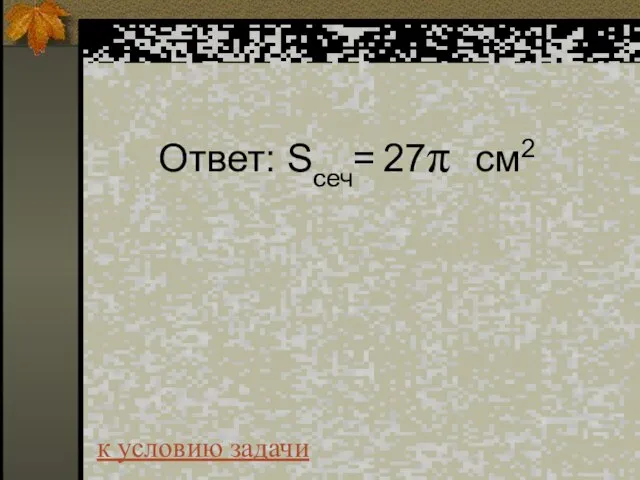
Ответ: Sсеч= 27π см2
к условию задачи

к условию задачи
М
О1
О
6 см

Дано:
Шар
R=10 см
α - секущая плоскость,
диаметр сечения = 12 см.
к условию задачи

найти:
d - расстояние от точки О до α.
к условию задачи

Решение:
т.к. диаметр круга в сечении равен 12 см, то радиус круга равен 6 см.
ОО1 ⊥ α, ОМ ∈ α, значит ОО1⊥ О1М.
треугольник ОО1М - прямоугольный, d= ОМ2 – МО12
d= 100 - 36 =8 см
к условию задачи

Ответ: d = 8 см.
к условию задачи

к условию задачи
М
О1
О
10 см

Дано:
Сфера,
R=13 см
α – секущая плоскость,
Длина линии пересечения сферы и α =10π см.
к условию задачи

найти:
d - расстояние от точки О до α.
к условию задачи

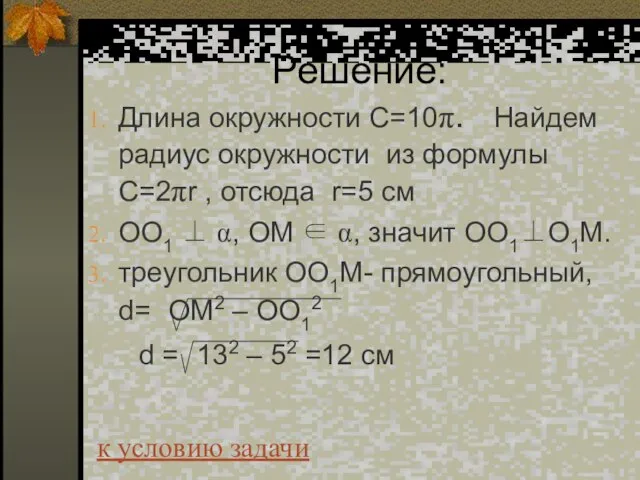
Решение:
Длина окружности С=10π. Найдем радиус окружности из формулы C=2πr , отсюда r=5 см
ОО1 ⊥ α, ОМ ∈ α, значит ОО1⊥О1М.
треугольник ОО1М- прямоугольный, d= ОМ2 – ОО12
d = 132 – 52 =12 см
к условию задачи

Ответ:d = 12 см.
к условию задачи

к условию задачи
М
О1
О
13 см

Дано:
Шар,
α - секущая плоскость, проходящая на расстоянии d=12 см от центра О.
Sсеч =25π см2
к условию задачи

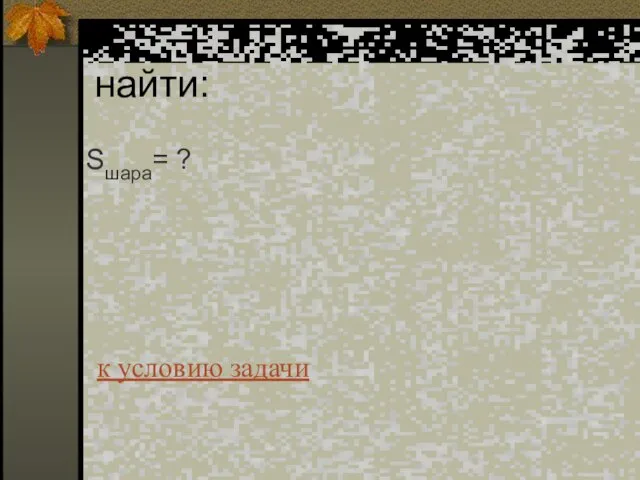
найти:
Sшара= ?
к условию задачи

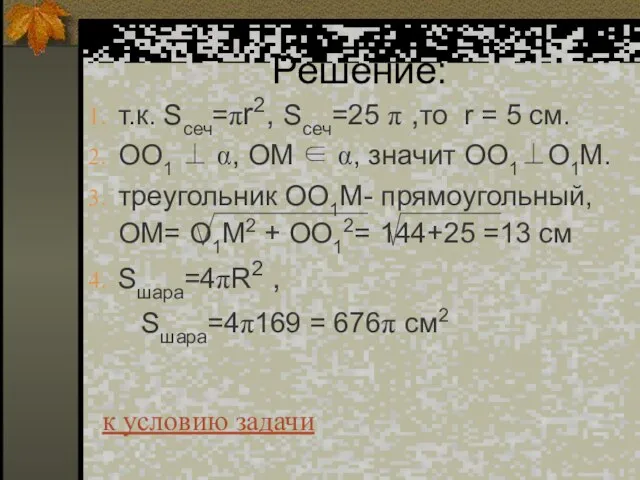
Решение:
т.к. Sсеч=πr2, Sсеч=25 π ,то r = 5 cм.
ОО1 ⊥ α, ОМ ∈ α, значит ОО1⊥О1М.
треугольник ОО1М- прямоугольный, ОМ= О1М2 + ОО12= 144+25 =13 см
Sшара=4πR2 ,
Sшара=4π169 = 676π см2
к условию задачи

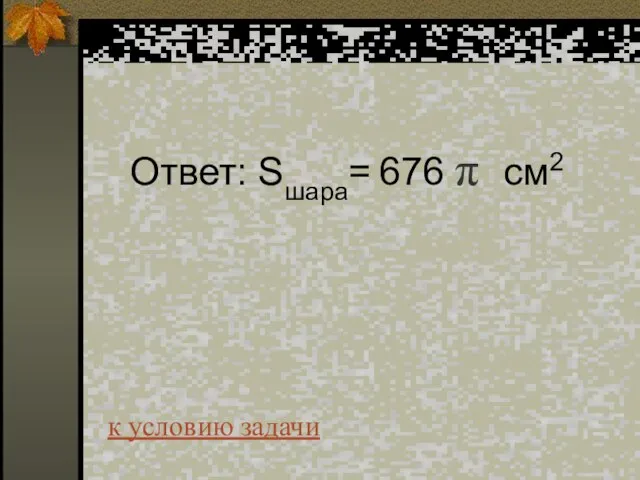
Ответ: Sшара= 676 π см2
к условию задачи

М
О1
О
R
к условию задачи
12 см

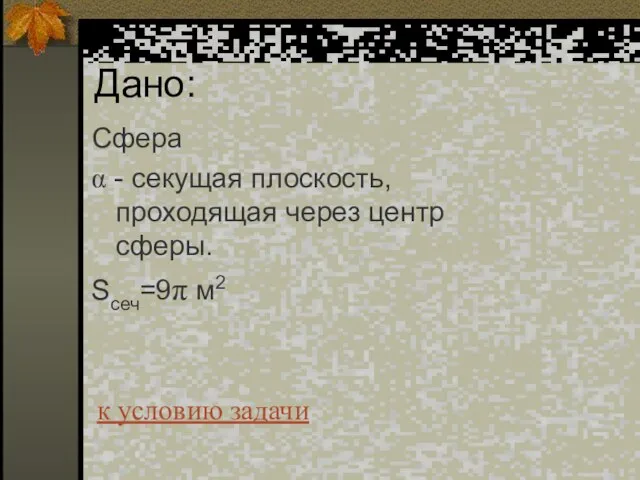
Дано:
Сфера
α - секущая плоскость, проходящая через центр сферы.
Sсеч=9π м2
к условию задачи

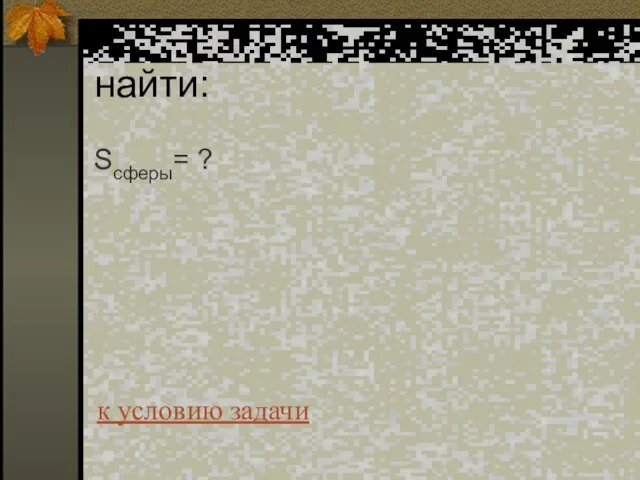
найти:
Sсферы= ?
к условию задачи

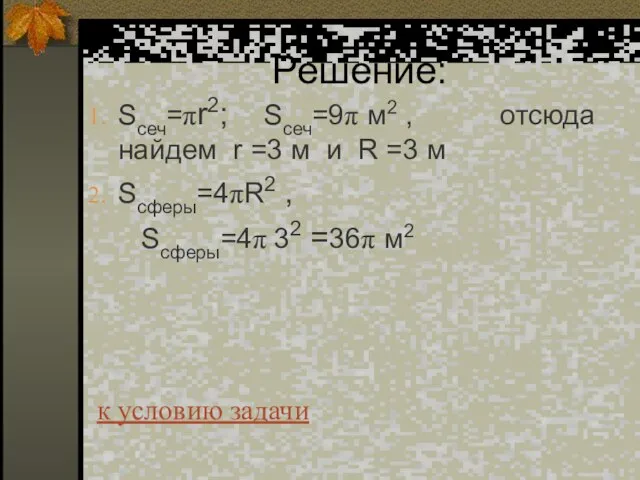
Решение:
Sсеч=πr2; Sсеч=9π м2 , отсюда найдем r =3 м и R =3 м
Sсферы=4πR2 ,
Sсферы=4π 32 =36π м2
к условию задачи

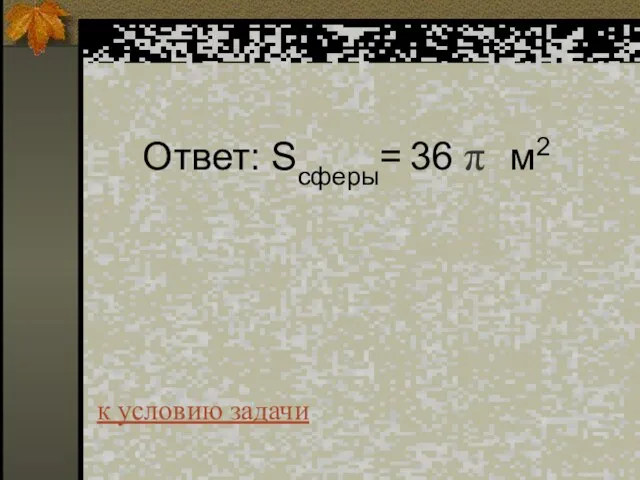
Ответ: Sсферы= 36 π м2
к условию задачи

О
к условию задачи
R r

Дано:
Шар
R=13 см
Две параллельные секущие плоскости, радиусами
5 см и 12 см.
к условию задачи

найти:
Расстояние между этими плоскостями.
к условию задачи

Решение:
Возможны 2 случая: 1) α1 и α2 расположены по разные стороны от центра; 2) α1 и α2 расположены по одну сторону от центра.
Рассмотрим треугольник ОО1А1 - прямоугольный, ОО1= 132 – 122 =5 см из треугольника ОО2А2 найдем ОО2= 132 – 52 =12 см
Для 1 случая: расстояние между плоскостями равно (12 + 5) см = 17 см
Для 2 случая: расстояние между плоскостями равно (12 - 5) см = 7 см
к условию задачи

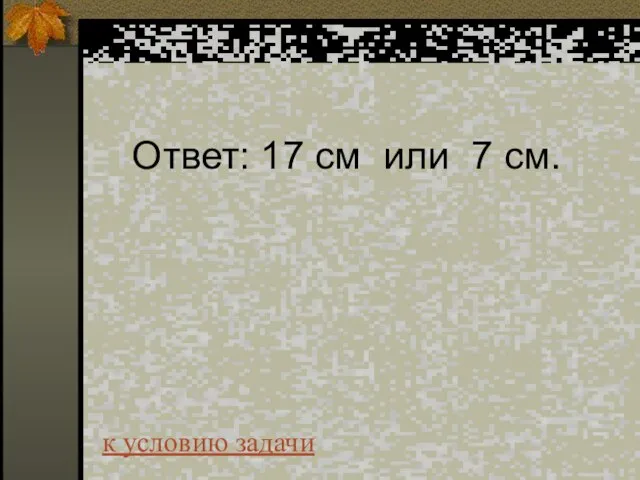
Ответ: 17 см или 7 см.
к условию задачи

О2
О
13 см
к условию задачи
О1
А2
А1
d2
d1

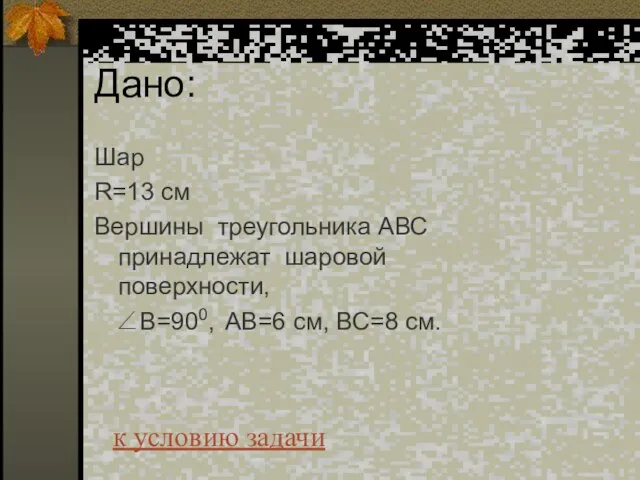
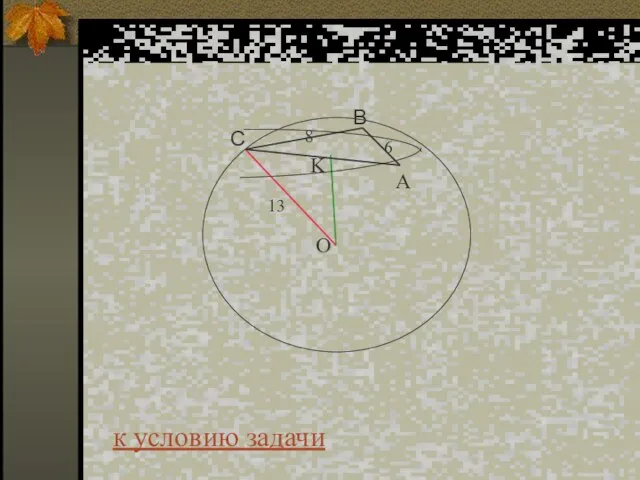
Дано:
Шар
R=13 см
Вершины треугольника АВС принадлежат шаровой поверхности,
∠B=900, AB=6 см, ВС=8 см.
к условию задачи

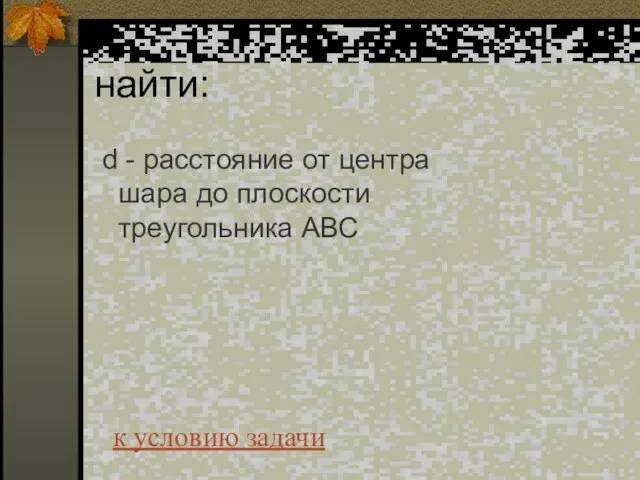
найти:
d - расстояние от центра шара до плоскости треугольника АВС
к условию задачи

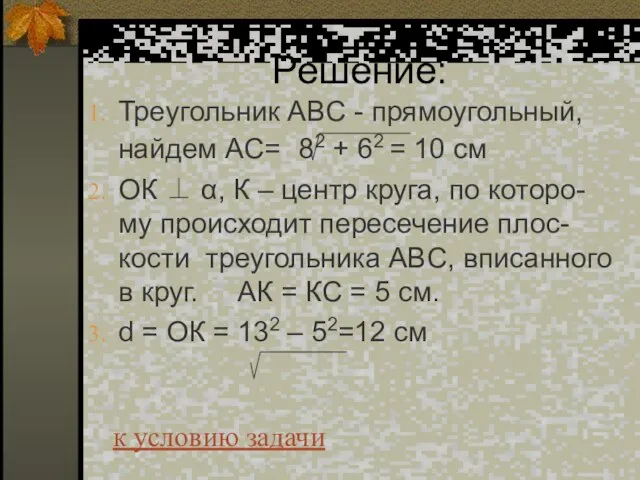
Решение:
Треугольник АBC - прямоугольный, найдем АС= 82 + 62 = 10 см
ОК ⊥ α, К – центр круга, по которо-му происходит пересечение плос-кости треугольника АBC, вписанного в круг. АК = КС = 5 см.
d = ОК = 132 – 52=12 см
к условию задачи

Ответ: d = 12 см.
к условию задачи

A
О
K
к условию задачи
C
B
13
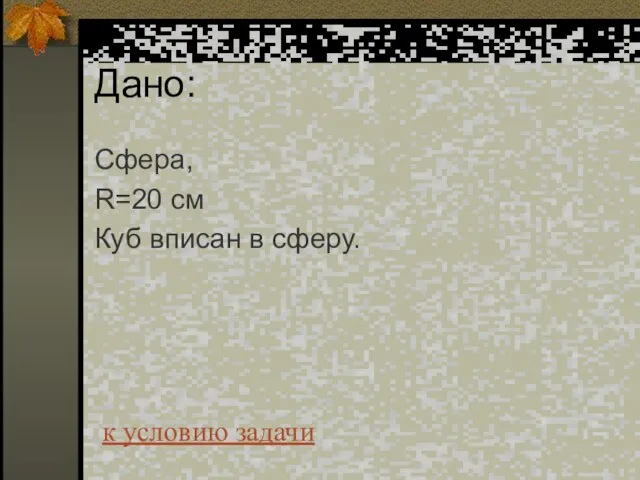
6
8

Дано:
Сфера,
R=20 см
Куб вписан в сферу.
к условию задачи

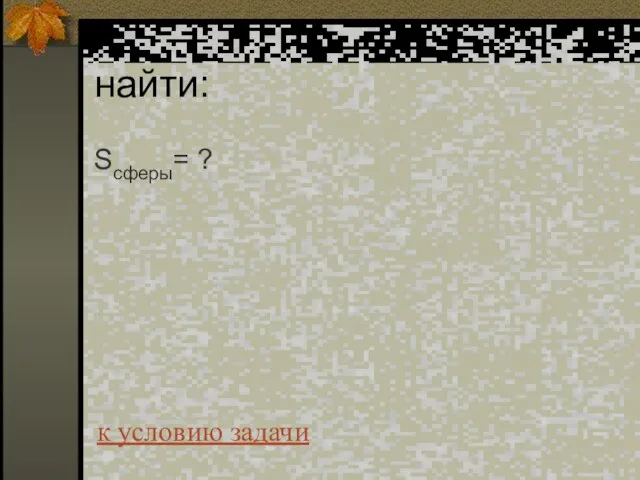
найти:
Sповерхности куба= ?
к условию задачи

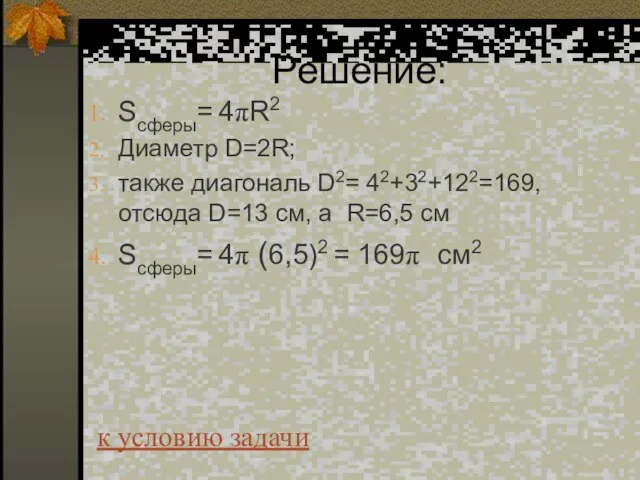
Решение:
Sпов куба= 6a2
т.к. D – диаметр шара; то D=2R; D=40 см.
с другой стороны D - диагональ вписанного куба, следовательно D2=a2+a2+a2=3а2, отсюда а2=D2:3, следовательно Sпов куба= 6(D2:3) = 2D2; Sпов куба= 3200 см2
к условию задачи

Ответ: Sпов. куба= 3200 см2
к условию задачи

к условию задачи
а
D

Дано:
сфера описана около прямоугольного параллелепипеда с измерениями:
а = 3 см в = 4 см
с = 12 см.
к условию задачи

найти:
Sсферы= ?
к условию задачи

Решение:
Sсферы= 4πR2
Диаметр D=2R;
также диагональ D2= 42+32+122=169, отсюда D=13 см, а R=6,5 см
Sсферы= 4π (6,5)2 = 169π см2
к условию задачи

Ответ: Sсферы= 169π см2
к условию задачи

к условию задачи
12
D
4
3