Содержание
- 2. Линию следует рассматривать как множество последовательных положений точки, перемещающейся в пространстве
- 3. Прямая
- 4. Прямая линия получается при прямолинейном движении точки без изменения направления движения
- 5. Совокупность элементов, задающих прямую в пространстве, называется определителем прямой
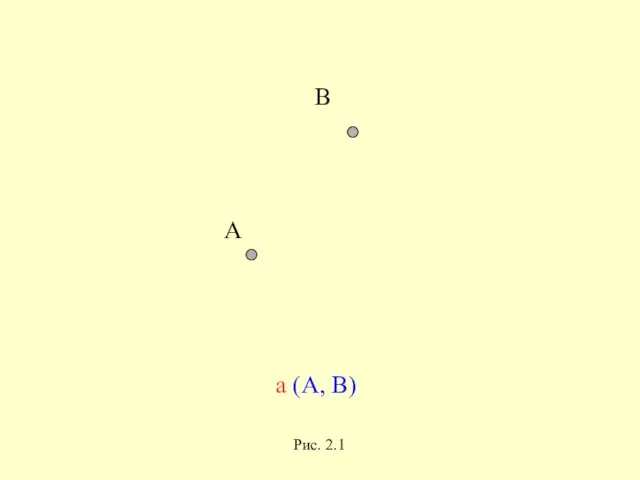
- 6. А В а (А, В) Рис. 2.1
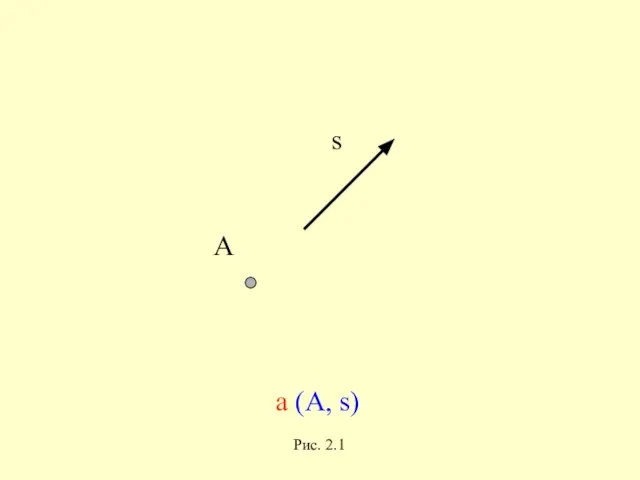
- 7. А s а (А, s) Рис. 2.1
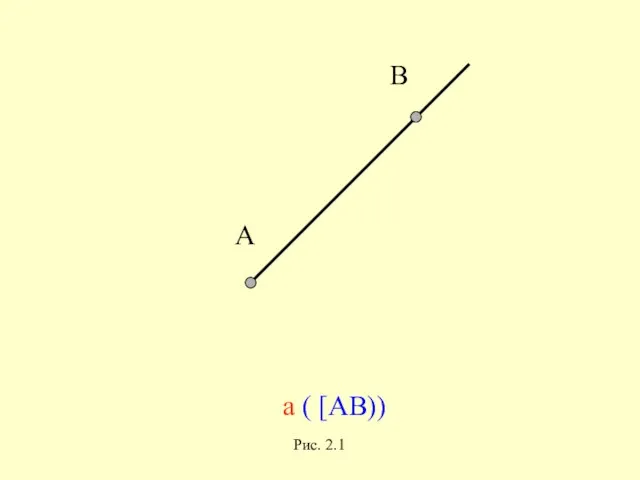
- 8. А В а ( [АВ] ) Рис. 2.1
- 9. А В а ( [АВ)) Рис. 2.1
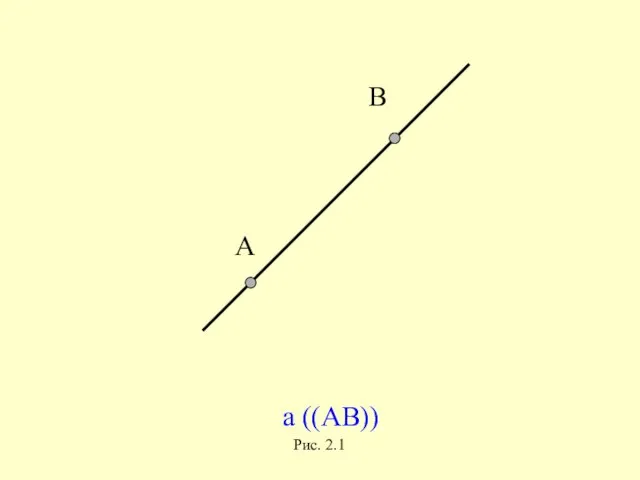
- 10. А В а ((АВ)) Рис. 2.1
- 11. Основные свойства прямоугольного проецирования: Точка проецируется в точку, прямая – в прямую, плоская фигура – в
- 12. Отсюда следует – для определения проекций прямой достаточно знать проекции двух не тождественных точек, принадлежащих прямой
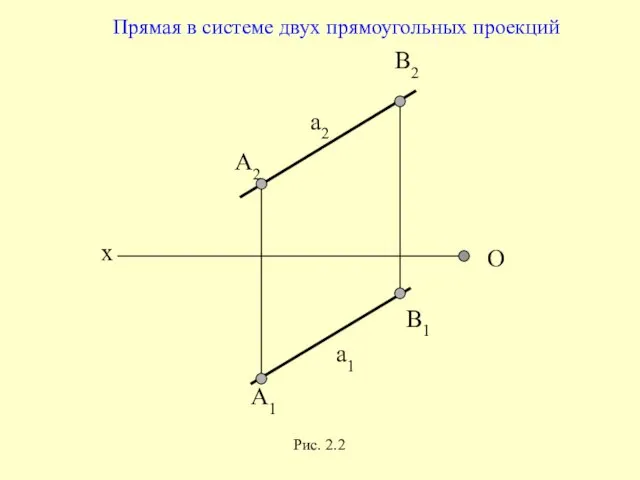
- 13. х О А2 В2 а2 А1 В1 а1 Прямая в системе двух прямоугольных проекций Рис. 2.2
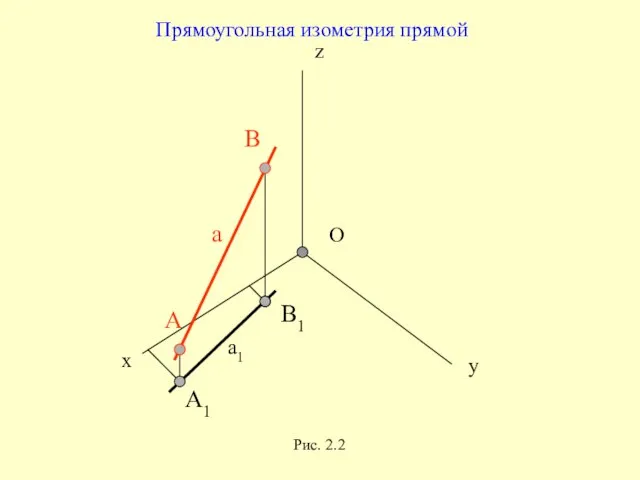
- 14. z x y O А1 В1 В А а а1 Прямоугольная изометрия прямой Рис. 2.2
- 15. Положение прямой относительно плоскостей проекций
- 16. Прямая общего положения – прямая, не перпендикулярная ни одной из плоскостей проекций
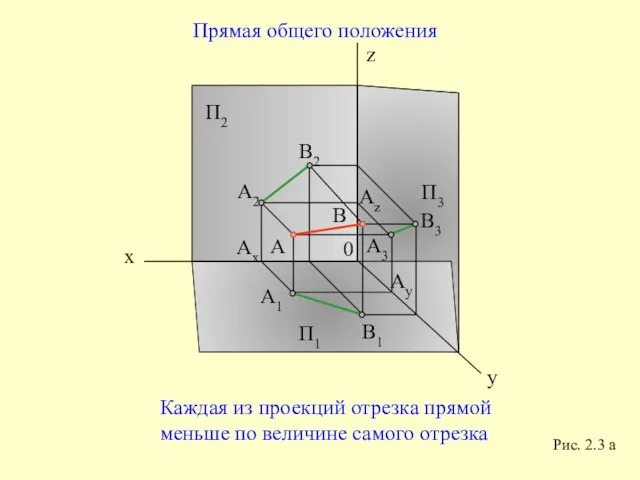
- 17. x z y П1 П2 П3 0 Прямая общего положения Каждая из проекций отрезка прямой меньше
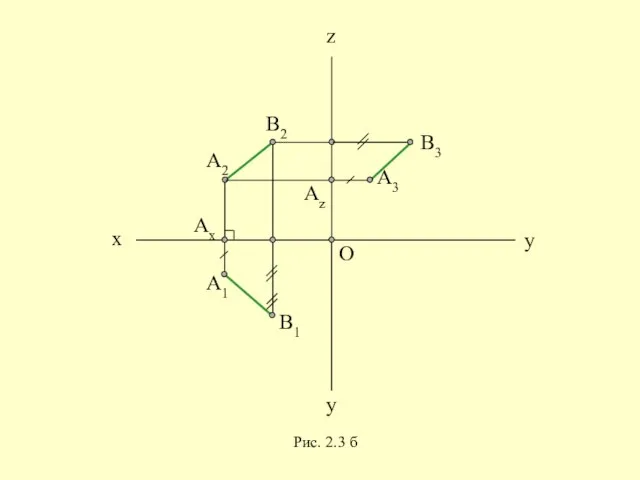
- 18. Рис. 2.3 б О х у z у
- 19. Прямая уровня - прямая, параллельная одной плоскости проекций
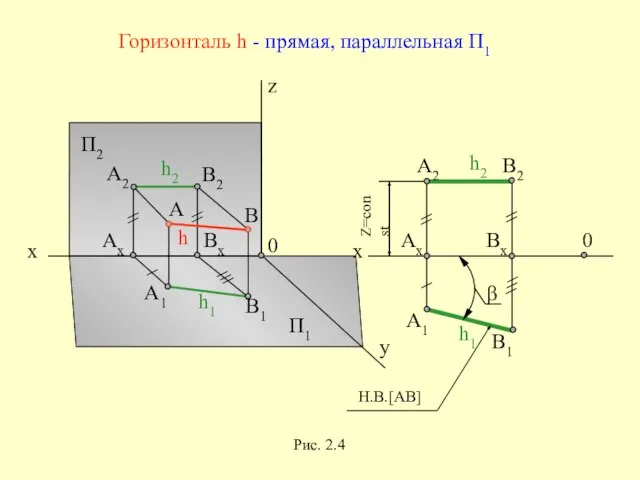
- 20. x z y П2 П1 x 0 0 Горизонталь h - прямая, параллельная П1 Рис. 2.4
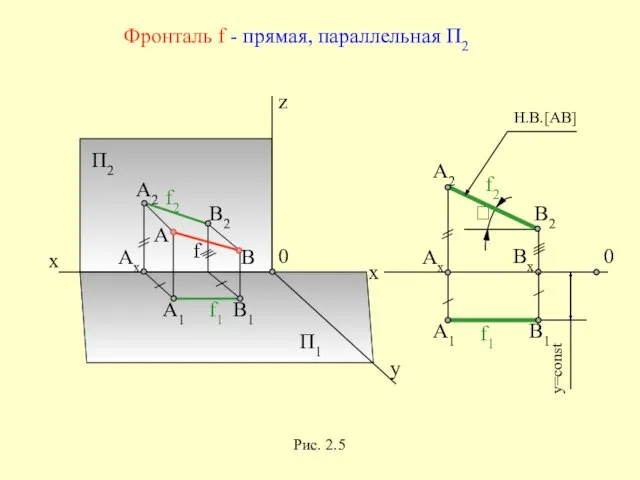
- 21. x z y П2 П1 0 x 0 Фронталь f - прямая, параллельная П2 Рис. 2.5
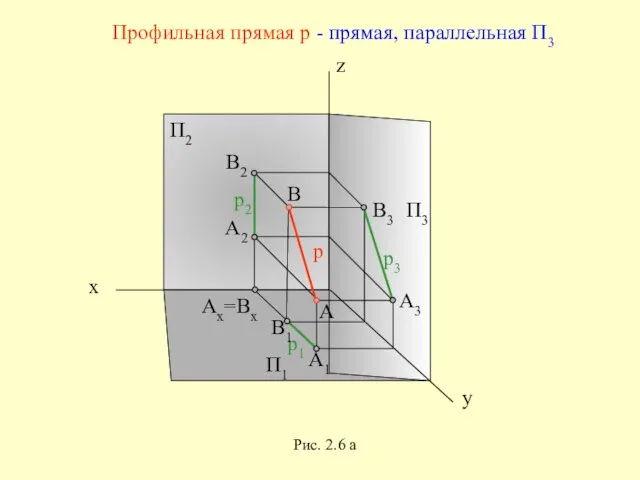
- 22. x z y П1 П2 П3 Профильная прямая р - прямая, параллельная П3 Рис. 2.6 а
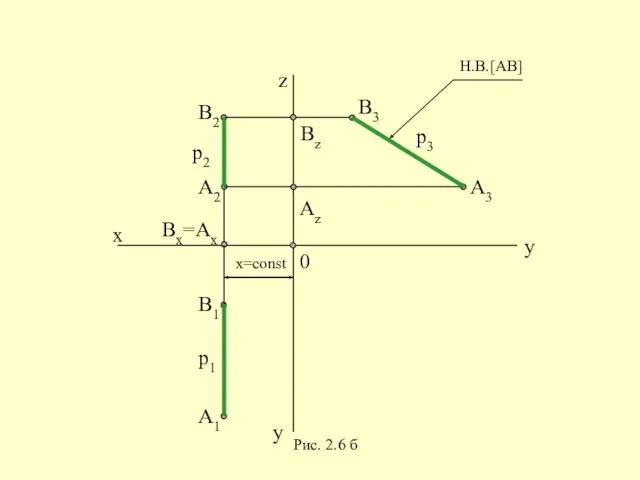
- 23. x y z y 0 Рис. 2.6 б
- 24. Вывод: Если отрезок лежит на прямой уровня (прямой, параллельной одной плоскости проекций), то он проецируется на
- 25. Проецирующие прямые - прямые, перпендикулярные одной из плоскостей проекций
- 26. x z y П2 П1 x 0 0 Горизонтально-проецирующая прямая - прямая, перпендикулярная П1 а1 -
- 27. x z y П2 П1 x 0 0 = a2 a1 Фронтально-проецирующая прямая - прямая, перпендикулярная
- 28. x П1 П2 П3 y z 0 Профильно-проецирующая прямая - прямая, перпендикулярная П3 Рис. 2.9 а
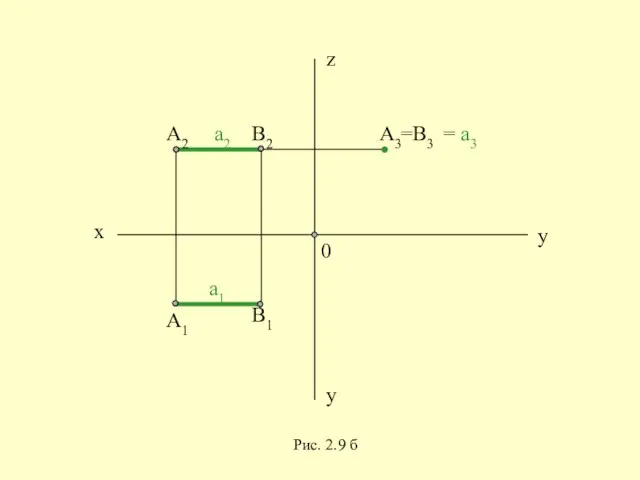
- 29. x y z y 0 =B3 Рис. 2.9 б
- 30. Вывод: Если прямая перпендикулярна какой-нибудь плоскости проекций, то на эту плоскость проекций она проецируется в точку
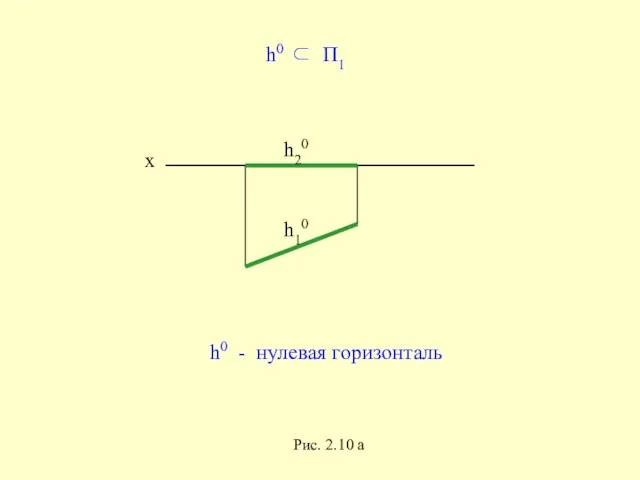
- 31. h20 h10 h0 ⊂ П1 x h0 - нулевая горизонталь Рис. 2.10 а
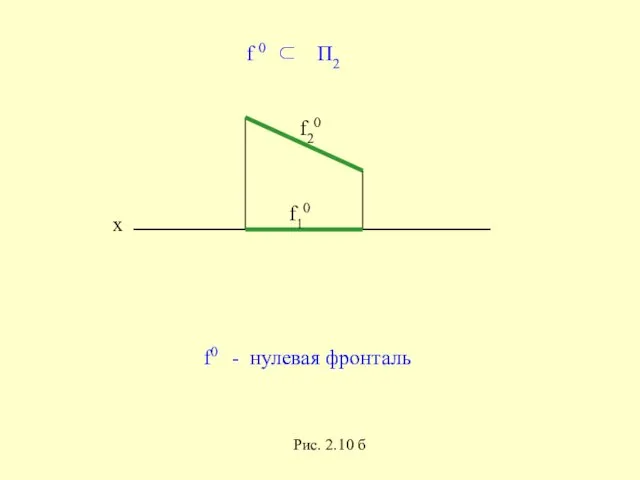
- 32. x f20 f10 f 0 ⊂ П2 f0 - нулевая фронталь Рис. 2.10 б
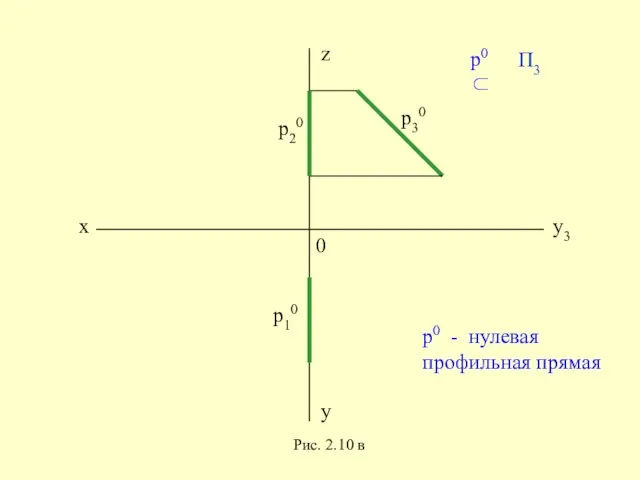
- 33. p30 p20 p10 0 x y z y3 p0 ⊂ р0 - нулевая профильная прямая Рис.
- 34. Точка на прямой
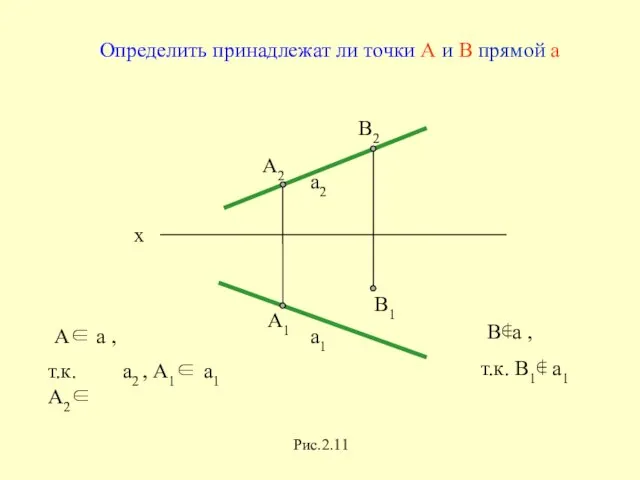
- 35. Точка принадлежит прямой, если проекция этой точки принадлежит проекции этой прямой
- 36. x a2 a1 A∈ a , В∉a , т.к. В1∉ a1 Рис.2.11 Определить принадлежат ли точки
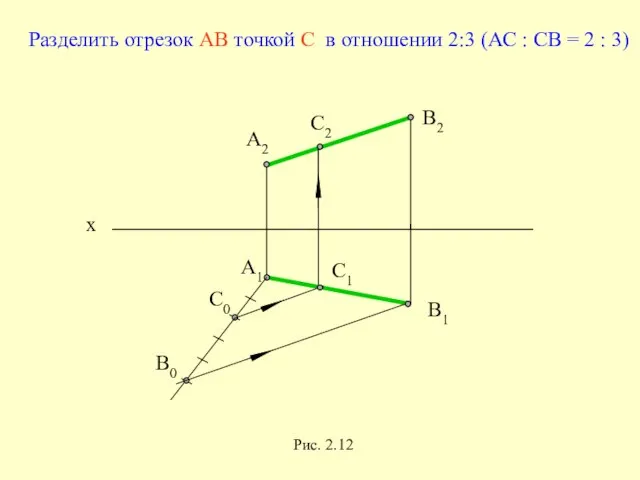
- 37. x A1 B1 A2 B2 Рис. 2.12 Разделить отрезок АВ точкой С в отношении 2:3 (АС
- 38. Следы прямой
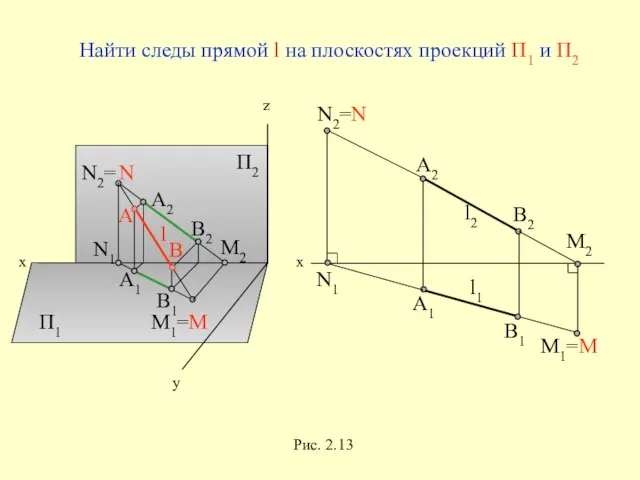
- 39. Точки пересечения прямой линии с координатными плоскостями проекций называются следами прямой
- 40. x z y П1 П2 М1= N2= A2 B2 A1 B1 х l2 l1 Рис. 2.13
- 41. x h2 h1 Рис. 2.14 Построение фронтального следа N горизонтали h
- 42. Взаимное положение прямых
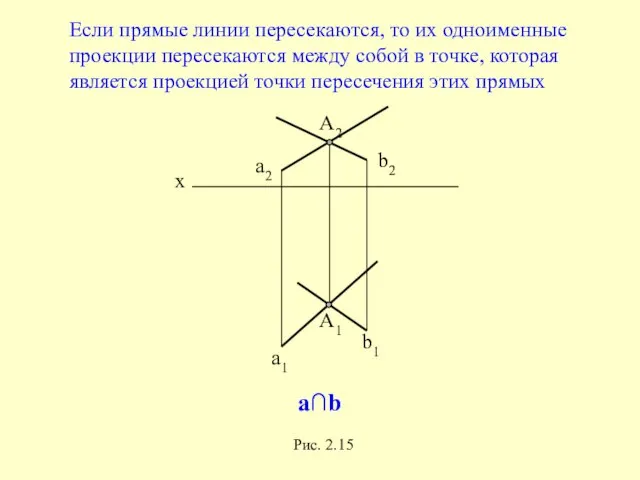
- 43. x a1 b1 b2 a2 Если прямые линии пересекаются, то их одноименные проекции пересекаются между собой
- 44. x a1 b1 b2 a2 Проекции параллельных прямых параллельны a || b Рис. 2.16
- 45. x a1 b1 b2 a2 a∸b Скрещивающиеся прямые Рис. 2.17
- 46. Плоские кривые
- 47. Кривые, все точки которых принадлежат одной плоскости, называют плоскими
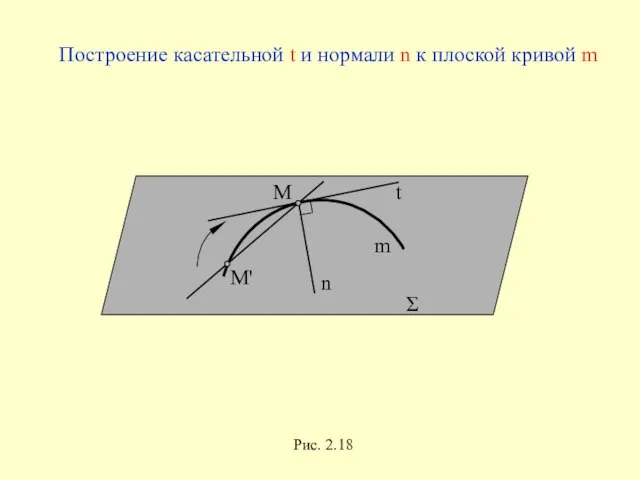
- 48. m Σ Рис. 2.18 Построение касательной t и нормали n к плоской кривой m
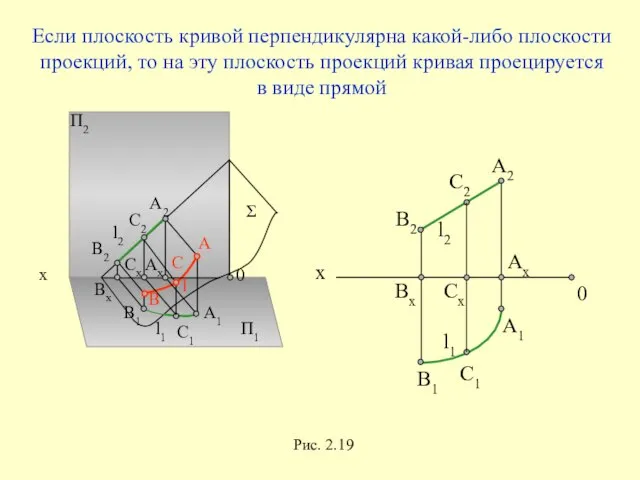
- 49. П2 П1 l2 l1 l x A2 B2 B1 А1 В Σ А 0 С2 С
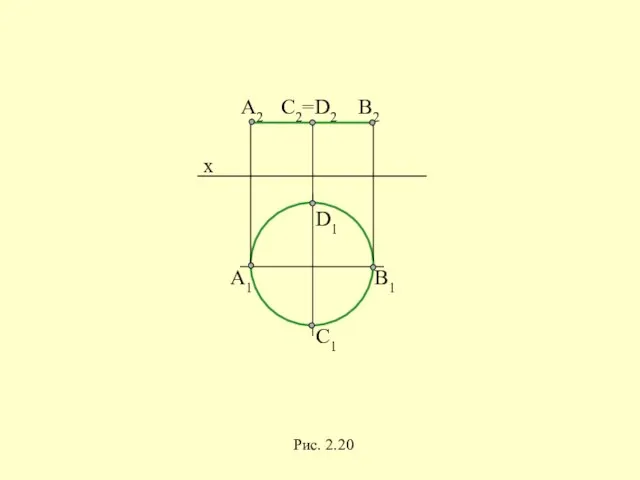
- 50. x D1 C1 A1 B1 A2 C2=D2 B2 Рис. 2.20
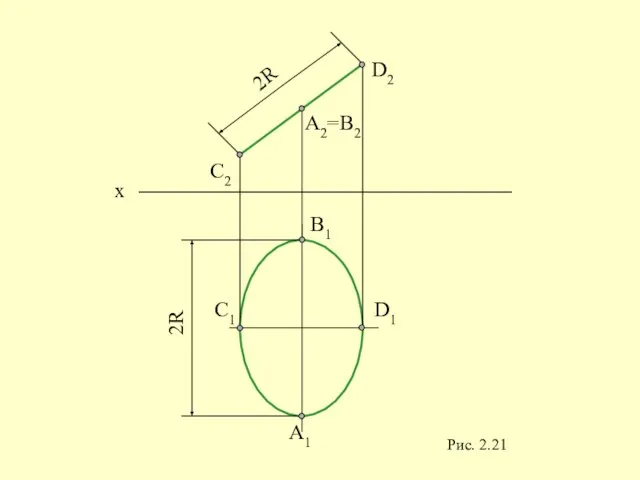
- 51. 2R 2R A1 C1 D1 B1 A2=B2 D2 C2 x Рис. 2.21
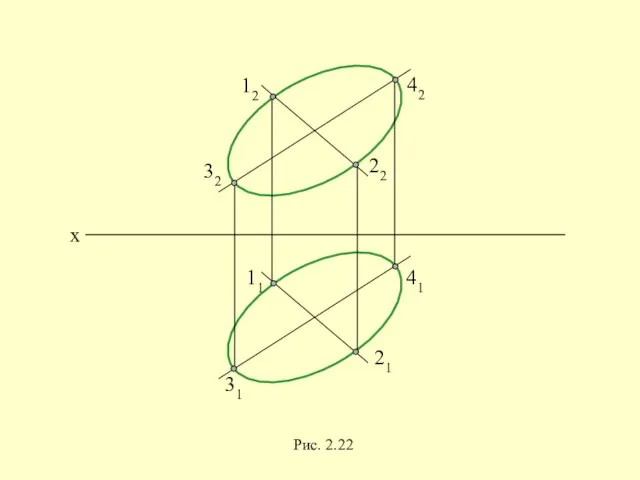
- 52. 11 21 31 41 12 22 32 42 x Рис. 2.22
- 53. Пространственные кривые
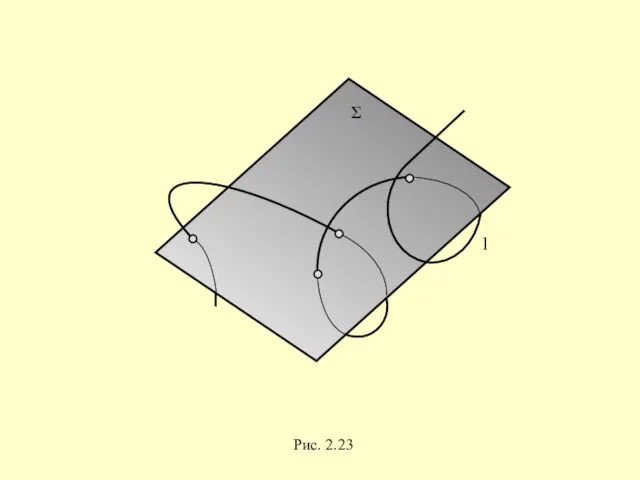
- 54. Кривые, все точки которых не принадлежат одной плоскости, называются пространственными
- 55. Σ l Рис. 2.23
- 57. Скачать презентацию




![А В а ( [АВ] ) Рис. 2.1](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/838779/slide-7.jpg)























 Компьютер и здоровье глаз
Компьютер и здоровье глаз Пейзаж.Времена года
Пейзаж.Времена года Организационное и информационное обеспечение фандрейзинга
Организационное и информационное обеспечение фандрейзинга Сложноподчиненное предложение. Повторение и обобщение изученного.
Сложноподчиненное предложение. Повторение и обобщение изученного. История радио и мобильной связи
История радио и мобильной связи А как ты знаешь физику?
А как ты знаешь физику? Презентация на тему Нефтяная промышленность
Презентация на тему Нефтяная промышленность  Изобразительное искусство барокко
Изобразительное искусство барокко Как начать бизнес в интернете?
Как начать бизнес в интернете? Sony Ericsson: Из VGA в HD
Sony Ericsson: Из VGA в HD Символика Краснодарского края
Символика Краснодарского края Для умных женщин Одна супружеская пара поехала в выходные на озеро порыбачить.
Для умных женщин Одна супружеская пара поехала в выходные на озеро порыбачить. Бюджет для граждан по Решению Совета депутатов МО Александровский район от 23.12.2020
Бюджет для граждан по Решению Совета депутатов МО Александровский район от 23.12.2020 Children's behavior and its influence on their future acts
Children's behavior and its influence on their future acts РАНХиГС_очно_27.09.2022_Акцнт, реф, защ, техн ОС
РАНХиГС_очно_27.09.2022_Акцнт, реф, защ, техн ОС Слова-паразиты, или экология речи
Слова-паразиты, или экология речи Иммунная система и канцерогенез
Иммунная система и канцерогенез  Подарки AI Journey. Предложения. Сберклауд
Подарки AI Journey. Предложения. Сберклауд Философские теории неврозов
Философские теории неврозов Реализация и изучение игры «Жизнь» в среде электронных таблиц (MS Ecxel)
Реализация и изучение игры «Жизнь» в среде электронных таблиц (MS Ecxel) Деструктивность учащегося и образовательной среды: точки соприкосновения
Деструктивность учащегося и образовательной среды: точки соприкосновения БАЛАНС-2W: ПОДГОТОВКА СПРАВКИ 2-НДФЛ
БАЛАНС-2W: ПОДГОТОВКА СПРАВКИ 2-НДФЛ Подготовка граждан к военной службе
Подготовка граждан к военной службе Ультразвуковые накладные расходомеры Flexim
Ультразвуковые накладные расходомеры Flexim Презентация для заказных проектов
Презентация для заказных проектов Поступление на государственную службу
Поступление на государственную службу Оценка достижений учащихся в разновозрастной группе
Оценка достижений учащихся в разновозрастной группе Grand Canyon National Park
Grand Canyon National Park