Объёмы тел

Если бы я родился музыкантом,
Я бы стремился перебороть шумы мира
С помощью стройных звуков.
Если бы я родился архитектором,
Я бы строил людям не квартиры, а домашние очаги.
Я одарил бы их светом, цветом и тишиной,
Но поскольку я поэт,
Я хотел бы так же четко и ясно
Говорить на языке слов,
Как математики говорят на языке чисел.

Объёмы тел

Объём — количественная характеристика пространства, занимаемого телом или веществом. Объём тела или вместимость сосуда определяется его формой и линейными размерами

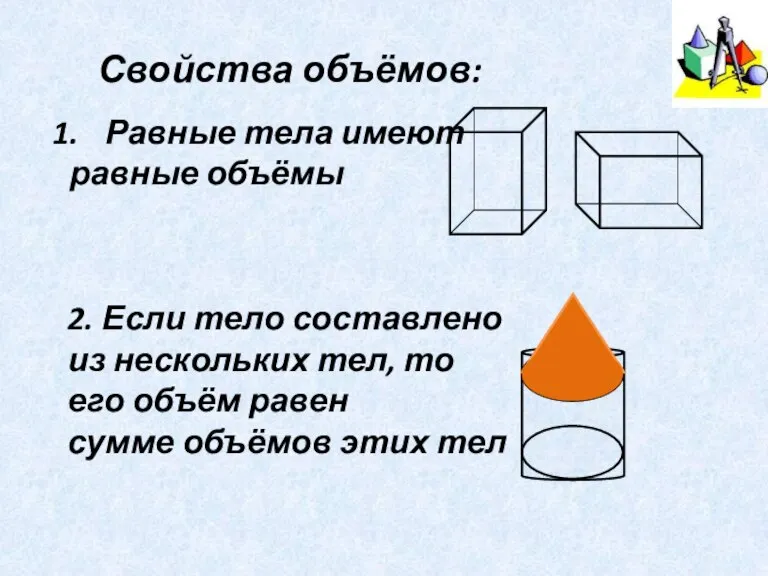
Свойства объёмов:
Равные тела имеют
равные объёмы

Симпсон Томас - английский математик. В 1743 вывел формулу приближённого интегрирования. В 1746 году Симпсон избран в члены Лондонского королевского общества, а ранее — в члены основанного в 1717 году в Лондоне Математического общества. Назначенный профессором в Вульвич, Симсон составил учебники по элементарной математике. В особых отделах геометрии рассматриваются задачи о наибольших и наименьших величинах, решаемые с помощью элементарной геометрии, правильные многогранники, измерение поверхностей, объёмы тел и, наконец, смешанные задачи.

Формула Симпсона
b, a – предельные значения высоты геометрического тела, среднее сечение – сечение тела плоскостью, параллельной основанию, и проходящей через середину высоты

Как найти объем у куба?
Есть у куба 3 стены,
В них по три величины.
Я возьму их, перемножу.
Ведь не так все это сложно.
С первой стенки взял длину,
Со второй взял ширину,
С третьей вышла высота.
Получилась красота!

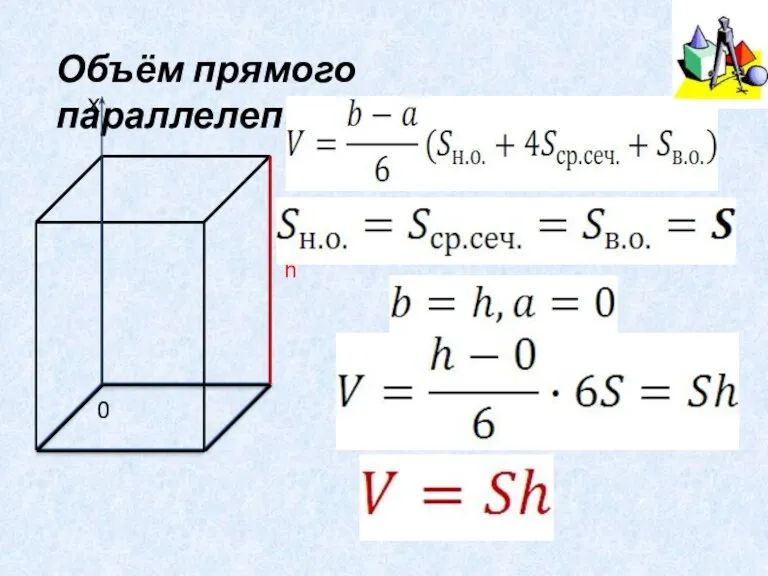
Объём прямого параллелепипеда.
h

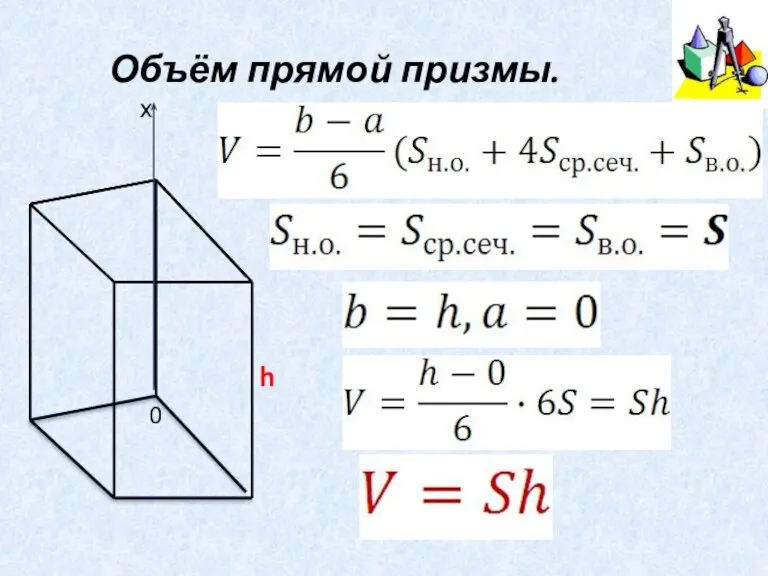
Объём прямой призмы.
h

-Цилиндр, что такое? - спросил я у папы.
Отец рассмеялся : - Цилиндр, это шляпа.
Чтобы иметь представление верное,
Цилиндр, скажем так, это банка консервная.
Труба парохода- цилиндр,
Труба на нашей крыше - тоже,
Все трубы на цилиндр похожи.
А я привёл пример такой -
Калейдоскоп любимый мой,
Глаз от него не оторвёшь,
И тоже на цилиндр похож.

Объём цилиндра.
h

Я видел картину. На этой картине
Стоит ПИРАМИДА в песчаной пустыне.
Всё в пирамиде необычайно,
Какая-то
есть в ней загадка и тайна.
А Спасская башня на площади Красной
И детям, и взрослым знакома прекрасно.
Посмотришь на башню, обычная с виду,
А что на вершине у ней? Пирамида!

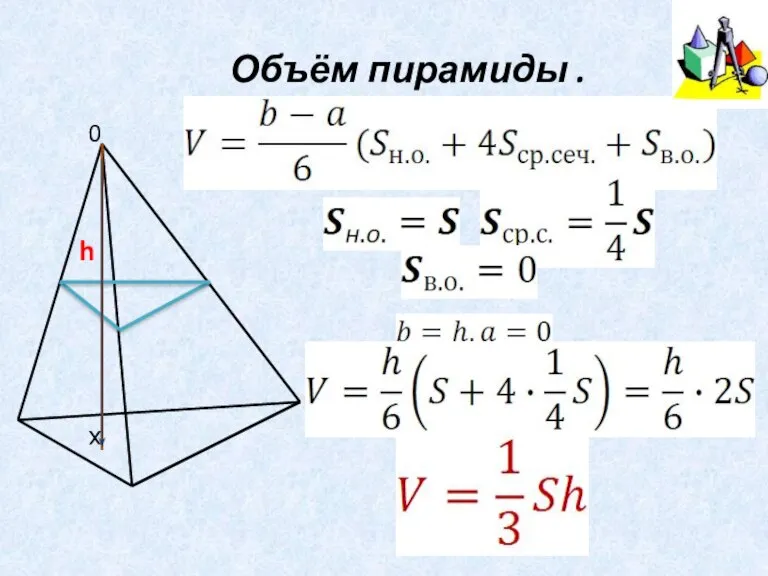
Объём пирамиды .

Сказала мама: - А сейчас
Про конус будет мой рассказ.
В высокой шапке звездочёт
Считает звёзды круглый год.
КОНУС- шляпа звездочёта.
Вот какой он. Понял? То-то.
Мама у стола стояла
В бутылки масло разливала.
- Где воронка? Нет воронки.
Поищи. Не стой в сторонке.
-Мама, с места я не тронусь ,
Расскажи ещё про конус.
-Воронка и есть в виде конуса лейка.
Ну-ка, найди мне её поскорей-ка.
Воронку я найти не смог,
Но мама сделала кулёк,
Картон вкруг пальца обкрутила
И ловко скрепкой закрепила.
Масло льётся, мама рада,
Конус вышел то, что надо.

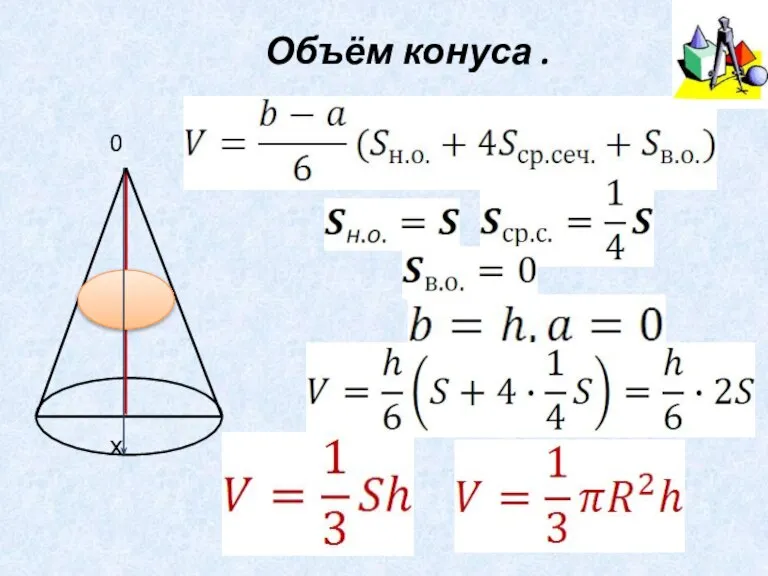
Объём конуса .

Удар! Удар! Ещё удар!
Летит в ворота мячик - ШАР!
А это- шар арбузный
Зелёный, круглый, вкусный.
Вглядитесь лучше - шар каков!
Он сделан из одних кругов.
Разрежьте на круги арбуз
И их попробуйте на вкус.

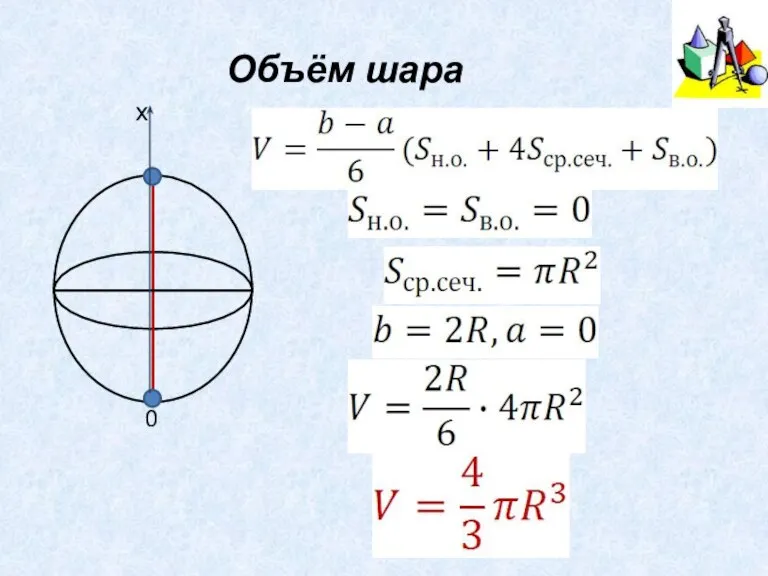
Объём шара

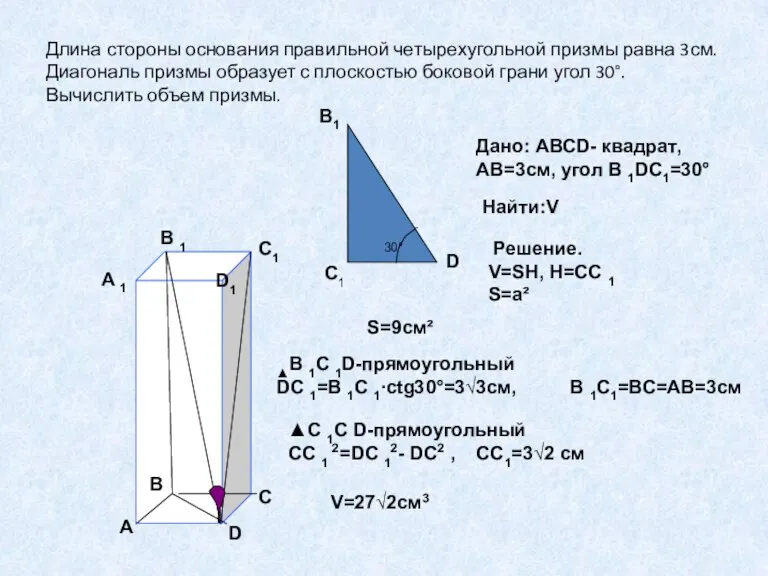
Длина стороны основания правильной четырехугольной призмы равна 3см. Диагональ призмы образует с плоскостью боковой грани угол 30°. Вычислить объем призмы.
А
В
С
D
A 1
B 1
C1
D1
C1
B1
D
30°
Дано: АВСD- квадрат, АВ=3см, угол В 1DC1=30°
Найти:V
Решение.
V=SH, H=СС 1
S=a²
S=9cм²
▲В 1С 1D-прямоугольный
DC 1=B 1C 1∙ctg30°=3√3см, В 1С1=ВС=АВ=3см
▲С 1С D-прямоугольный
СC 1 2=DC 12- DC2 , СС1=3√2 см
V=27√2см3

Практическая задача.
Надо найти объём воды проходящёй за день в водонапорной вышке такого типа:

Решение.
Во-первых это цилиндр. Объём цилиндра равен
Сложность тут может доставить нахождение радиуса, но только с практической точки зрения. R=L/2π, где L-длина окружности, которую можно измерить верёвочкой. Установив все данные, подставим в формулу объёма. Но это ещё не всё, теперь умножаем объём на количество полных закачек за день, и мы получим полный объём воды проходящей через водонапорную башню.

Задачник.
№1. Найдите объём правильной четырёхугольной пирамиды, если её диагональное сечение – равносторонний треугольник, площадь которого 12 √3
№2. В правильной четырёхугольной призме ABCDA’B’C’D’ высота в два раза длиннее стороны основания. Найдите объём призмы, если расстояние между серединами рёбер A’B’ и BC равно 3√2.
№3. Через две образующие конуса, угол между которыми равен 30° проведено сечение, имеющее площадь 25 дм². найти объём конуса, если радиус основания 6 дм.
№4. В конус вписан шар. Найти объём шара, если радиус основания конуса равен 3, а образующая равна 4.
№5. Через точку А, лежащую на окружности основания цилиндра, проведена прямая, пересекающая окружность второго основания в точке В. Радиус цилиндра равен 5, длина отрезка АВ равна 4√5, расстояние между осью цилиндра и прямой АВ равно 3. найти объём цилиндра.

Формулой Симпсона называется
интеграл от интерполяционного
многочлена второй степени на отрезке
где значения функции в соответствующих
точках (на концах отрезка и в его середине).
,
и
-
Получила название в честь британского математика Томаса Симпсона (1710—1761).