OE_02.1 (1)

Институт энергетики
и транспортных систем
Цель дисциплины – освоение методов анализа и расчета электрических и магнитных цепей, получение общего представления о теории электромагнитного поля.
Задача дисциплины – изучение магнитного поля и его проявлений в различных технических устройствах, усвоение современных методов анализа и расчета электрических цепей, электрических и магнитных полей, знание которых необходимо для успешной профессиональной деятельности.
Цели и задачи дисциплины «ОБЩАЯ ЭЛЕКТРОТЕХНИКА»

Институт энергетики
и транспортных систем
Курс лекций: ОБЩАЯ ЭЛЕКТРОТЕХНИКА
Сергей Юльевич Грачев
доц., к.т.н., кафедра «Электротехника и электроэнергетика», ИЭиТС

Институт энергетики
и транспортных систем
Структура курса
Однофазные электрические цепи
Трехфазные электрические цепи
Машины постоянного тока
Трансформаторы
Асинхронные двигатели
В результате изучения дисциплины студент должен:
знать: устройство, принцип действия, области применения основных электротехнических устройств и электроизмерительных приборов;
уметь: использовать инструкции, описания, технические паспорта о работе устройств и установок;
владеть: методикой расчета простейших электрических цепей.
Виды учебной работы: лекции и лабораторные работы
Изучение дисциплины заканчивается зачетом и экзаменом.

Институт энергетики
и транспортных систем
Комплексный метод расчета
Расчет токов и напряжений в цепях синусоидального тока с помощью методов, основанных на законах Кирхгофа, Ома, Фарадея, Джоуля—Ленца, значительно сложнее из-за необходимо­сти выполнения сложных действий с тригонометрическими фун­кциями. Трудности расчета облегчает применение комплексного метода, основанного на замене операций с синусоидальными функциями операциями с комплексными числами.

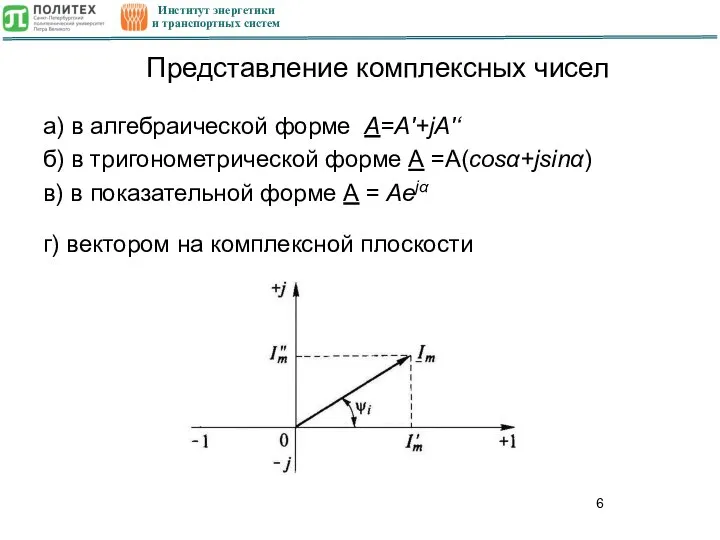
Институт энергетики
и транспортных систем
Представление комплексных чисел
а) в алгебраической форме A=A'+jA'‘
б) в тригонометрической форме A =A(cosα+jsinα)
в) в показательной форме A = Aejα
г) вектором на комплексной плоскости

Институт энергетики
и транспортных систем
Складывать и вычитать комплексные числа
А = А' + jA" и В = В' + jB
удобнее в алгебраической форме
А ± В = (А' + jA') ± (В' + jB') = (А' ± А') + j(B' ± В').
Умножать и делить комплексные числа легче в полярной фор­ме.
Если , а, то , .

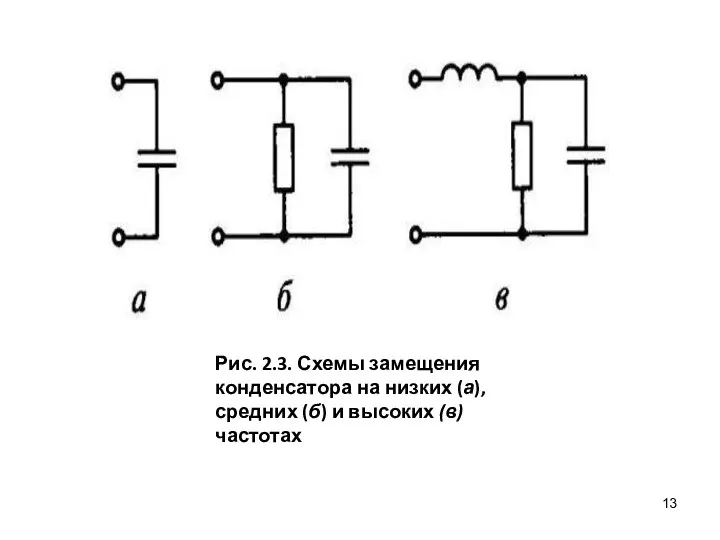
Идеальные элементы цепи переменного тока.
Схемы замещения реальных элементов
В реальных пассивных элементах электрической цепи (резисто­рах, конденсаторах и катушках индуктивности) при синусоидаль­ных токах происходят сложные процессы, связанные с накопле­нием и перераспределением электрической и магнитной энергии и преобразованием их в тепловую энергию. Поэтому их эквива­лентные схемы включают в себя идеальные резистивные, емкост­ные и индуктивные элементы.
Идеальный резистивный элемент — элемент схемы, в котором происходит необратимое преобразование электрической энергии в работу, теплоту или другой вид энергии. Идеальный резистив­ный элемент в цепи переменного тока изображается так же, как в цепи постоянного тока, — прямоугольником.

Институт энергетики
и транспортных систем
Реальные резистивные элементы — резисторы — изготовляют­ся из различных материалов и имеют разные конструкции. В зави­симости от конструкции создаются электрические и магнитные поля, в которых запасается энергия, т.е. резистор имеет дополни­тельно свойства индуктивного и емкостного элементов. На про­мышленной частоте эти составляющие малы, и ими можно пре­небречь, полагая резистор идеальным. На рис. 2.1 показаны схемы замещения резистора на различных частотах. Рабочим параметром реального резистора является сопротивление, а паразитными параметрами — емкость и индуктивность.

Институт энергетики
и транспортных систем
Идеальный индуктивный элемент --- элемент схемы, в котором запасается энергия магнитного поля. Идеальный индуктивный элемент в цепи переменного тока обозначается буквой L. Этой же буквой обозначается величина, численно равная отношению потокосцепления Ψ индуктивного элемента к току i и называемая индуктивностью L =Ψ/i.
1.1

Институт энергетики
и транспортных систем
1.1
Индуктивность является параметром идеального индуктивного элемента. Единицей индуктивности является генри (Гн). Отношение амплитуд или действующих значений напряжения и тока называется индуктивным сопротивлением и обозначается XL (XL=ULm/Im=UL/I).
При известных индуктивности L и угловой частоте ω индуктивное сопротивление XL =ωL. Величина BL, обратная XL, называется индуктивной проводимостью. Синусоидальный ток в индуктивном элементе отстает от напряжения на угол π/2 (или 90°). Если напряжение uL(t)=ULтsinωt, то ток i(t)=Imsin(ωt -- 90°). В комплексной форме ULm = jωLIm, или U = jωLI. Идеальный индуктивный элемент близок по свойствам к проволочной катушке, навитой из хорошо проводящей проволоки.
Рис. 2.2. Схемы замещения катушки индуктивности на низких (а), средних (б) и высоких (в) частотах

Институт энергетики
и транспортных систем
1.1
Понятия о токе, ЭДС и напряжении, предполагается, Вам известны из курса физики.
Синусоидальный ток в RL-цепи
Пусть в последовательно соединенных элементах R и L (рис. 4.9) ток изменяется по синусоидальному закону: I=Imsinωt.
Требуется найти напряжение u(t), т.е. его амплитуду Um и на­чальную фазу.
По второму закону Кирхгофа для рассматриваемой цепи и= uR+uL, где uR = Ri = =RImsinωt, uL=ωLIm sin(ωt +90°). С учетом этого получим u(t)=Uтsin(ωt+ φ) =RImsin(ωt + 90°).
Определить искомые амплитуду и начальную фазу напряжения можно с помощью векторной диаграммы.

Векторная диаграмма — это совокупность векторов, изобража­ющих на плоскости синусоидально изменяющиеся с одной и той же частотой величины. Каждый вектор вычерчивается на плоско­сти с учетом его начальной фазы, отсчитываемой от оси абсцисс.
Отложим из начала координат вектор тока (рис. 2.5, а). В том же направлении отложим вектор напряжения на резисторе, который совпадает по фазе с вектором тока. Из конца вектора напряжения на резисторе отложим вектор напряжения на катушке, который перпендикулярен вектору тока (т.е. составляет с вектором тока угол π/2), так как напряжение на катушке опережает протекаю­щий ток на угол π/2 (90°). Сумма этих векторов равна вектору напряжения, приложенному ко входу цепи.
Из треугольника напряжений , откуда искомая амплитуда напряжения

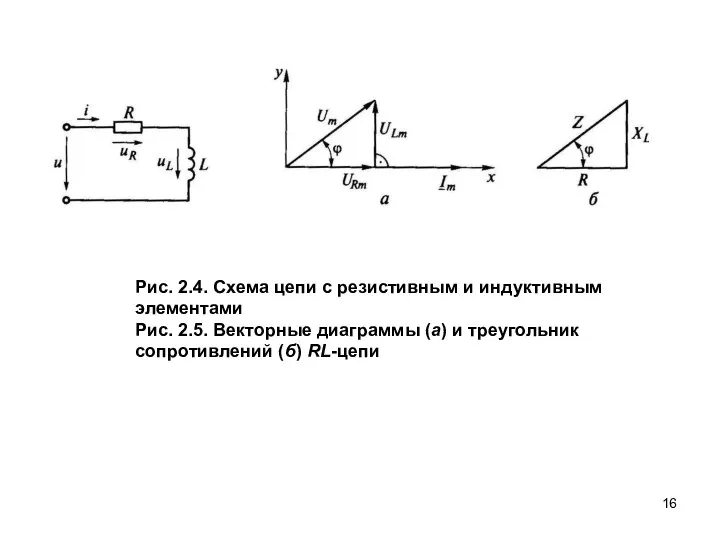
Рис. 2.4. Схема цепи с резистивным и индук­тивным элементами
Рис. 2.5. Векторные диаграммы (а) и тре­угольник сопротивлений (б) RL-цепи

Институт энергетики
и транспортных систем
1.1
Синусоидальный ток RС-цепи
Пусть к параллельно соединенным элементам R и С подклю­чен источник, питающий их напряжением u= Umsinωt (рис. 2.6). Требуется найти ток i(t), его амплитуду и сдвиг по фазе относи­тельно u(t).
По первому закону Кирхгофа i = iR+ iC,
где iR = IRmsinωt; iC =ICmsin(ωt + π/2), а IRm=Um/R= GUm; ICm = Um/XC=BC Um = ωCUm.
С учетом этого i(t)= GUmsinωt + ωCUmsin (ωt +π/2) = Imsin (ωt —φ).
Из треугольника токов (рис. 4.12, а) получим
откуда искомая амплитуда тока:
,
где Y— полная проводимость RC-цепи,
.

Рис. 2.6. Схема цепи с резистивным и емко­стным элементами
Рис. 2.7. Векторная диаграмма (а) и тре­угольник проводимостей (б) параллельной RC-цепи
Треугольнику токов соответствует треугольник проводимостей (рис. 2.7, б). Второй искомый параметр — сдвиг фаз — находим из простого тригонометрического соотношения для треугольника сопротивлений
.

Полное решение дифференциального уравнения состоит из двух частей: частного, когда u=0
Анализ процессов в цепи синусоидального тока при последовательном соединении элементов R, L, C
Пусть к последовательно соединенным элементам R, L и С приложено синусоидальное напряжение u= Umsinωt (рис. 2.8). Необходимо найти ток i(t), т.е. его амплитуду Im и сдвиг по фазе относительно напряжения u(t).
Для рассматриваемой цепи по второму закону Кирхгофа u=uR + uL + uC.
Из подразд. 4.4, 4.5 известно, что амплитуды напряжений на элементах связаны с током

Институт энергетики
и транспортных систем
И общего, описывающего установившийся процесс.
Запишем диффуравнение в комплексной форме:
(Ток в цепи существует во время переходного процесса, пока не израсходуются запас энергии)
1.1

Из полученных уравнений следует
Эти выражения представляют собой закон Ома в комплексной форме. Коэффициент Z в этих выражениях наз. комплексным сопротивлением
Из уравнения 2.5. следует

Институт энергетики
и транспортных систем
1.2
Как постоянный, так и синусоидальный токи исполь-зуются для совершения какой-либо работы, в процессе которой электроэнергия преобразуется в другие виды энергии (тепловую, механическую и т. д.). Для количественной оценки синусоидального тока (ЭДС и напряжения), который в течение времени непрерывно периодически изменяется, используют значение постоянного тока, эквивалентное значению синусоидального тока по совершаемой работе.

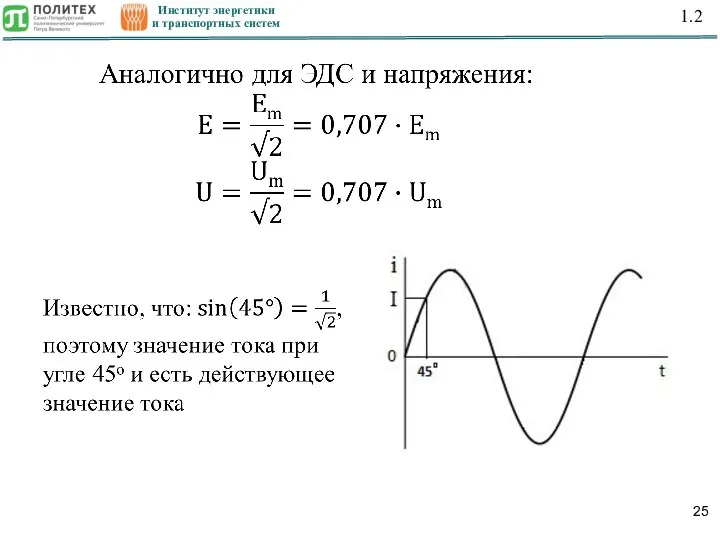
Институт энергетики
и транспортных систем
1.2
Действующее значение синусоидального тока

Институт энергетики
и транспортных систем
1.2

Институт энергетики
и транспортных систем
1.2
Под средним значением синусоидальной величины понимается ее среднеарифметическое значение. Но…
Среднее значение синусоидального тока
ЗАПОЛНИТЬ ДОМА!!!

Институт энергетики
и транспортных систем
1.2
Коэффициент характеризует «пиковость» кривой.
Чем больше Кф отличается от 1,
тем более «пиковый» характер носит кривая.
Коэффициент формы периодической кривой
Для периодической кривой, имеющей
прямоугольную форму: ?
Кф=1
I=Im=Iср
Домашнее задание: для какой
кривой Кф=1,21?

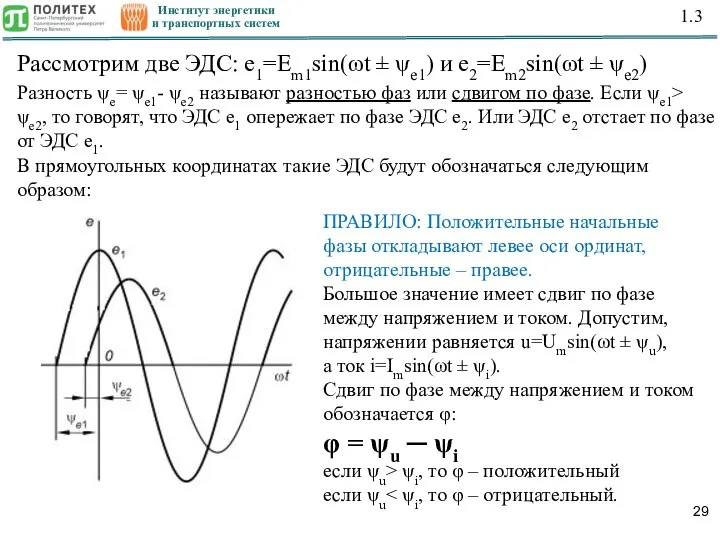
Институт энергетики
и транспортных систем
1.3
1.3. ИЗОБРАЖЕНИЕ СИНУСОИДАЛЬНЫХ ВЕЛИЧИН В ПРЯМОУГОЛЬНЫХ КООРДИНАТАХ
…совпадают по фазе (е1 и е2)
…находятся в противофазе (е1 и е3,
е2 и е3)
В общем случае синусоидальные величины могут не проходить через нулевые значения при t=0, тогда их записывают так:
i=Imsin(ωt ± ψi)
e=Emsin(ωt ± ψe)
u=Umsin(ωt ± ψu)
углы ψi, ψe, ψu – начальные фазы, т.е. фазы при t=0

Институт энергетики
и транспортных систем
1.3
Рассмотрим две ЭДС: e1=Em1sin(ωt ± ψe1) и e2=Em2sin(ωt ± ψe2)
Разность ψe= ψe1- ψe2 называют разностью фаз или сдвигом по фазе. Если ψe1> ψe2, то говорят, что ЭДС е1 опережает по фазе ЭДС е2. Или ЭДС е2 отстает по фазе от ЭДС е1.
ПРАВИЛО: Положительные начальные фазы откладывают левее оси ординат, отрицательные – правее.
Большое значение имеет сдвиг по фазе между напряжением и током. Допустим, напряжении равняется u=Umsin(ωt ± ψu),
а ток i=Imsin(ωt ± ψi).
Сдвиг по фазе между напряжением и током обозначается φ:
φ = ψu ─ ψi
если ψu> ψi, то φ – положительный
если ψu˂ ψi, то φ – отрицательный.
В прямоугольных координатах такие ЭДС будут обозначаться следующим образом:

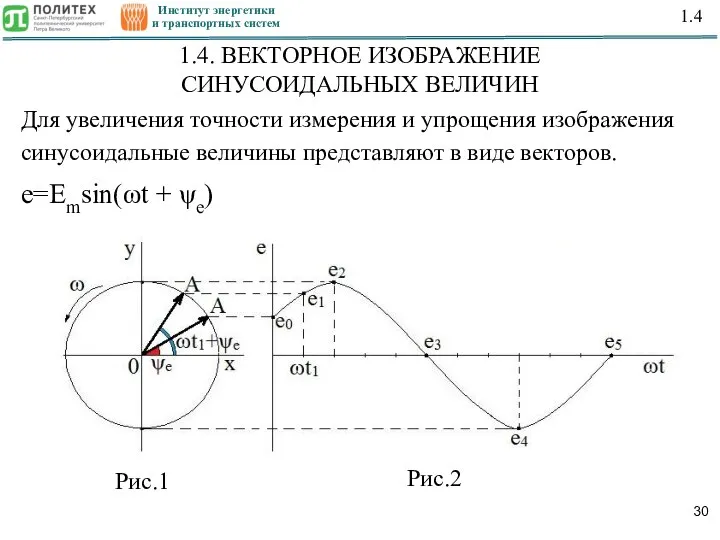
Институт энергетики
и транспортных систем
1.4
1.4. ВЕКТОРНОЕ ИЗОБРАЖЕНИЕ СИНУСОИДАЛЬНЫХ ВЕЛИЧИН
Для увеличения точности измерения и упрощения изображения синусоидальные величины представляют в виде векторов.
e=Emsin(ωt + ψe)
Рис.1
Рис.2

Институт энергетики
и транспортных систем
1.4
На рис.1 отложим вектор OA, длина которого равна
амплитуде ЭДС, под углом ψe (около 30°) к оси OX.
На рис.2 будем откладывать угол ωt по оси абсцисс,
а проекции вектора на ось OY – по оси ординат.
При t=0 проекция ОА на ось OY равна
OA∙sin( ψe) =Em∙sin(ψe)
где Em∙sin(ψe) есть мгновенное значение при t=0, т.е. e0.
Зададимся масштабом: 2 клетки (1 см) = 30°.
Будем вращать вектор OA с частотой ω в направлении против часовой стрелки. Пусть через время Δt вектор повернется на 30°.
Обозначим это время как t1.
При t1 проекция вектора OA на ось OY равна:
OA∙sin(ωt1 + ψe) = Em∙sin(ωt1 + ψe) = e1
где e1 – заданная ЭДС.

Институт энергетики
и транспортных систем
1.4
Повернем вектор OA ещё на 30° ─ проекция e2
ещё на 90° ─ проекция e3
ещё на 90° ─ проекция e4
ещё на 90° ─ проекция e5
e2 и e4 ─ когда вектор совпадает с осью OY,
проекция при этом равна длине вектора OA.
e3 и e5 ─ когда проекции вектора равны нулю.

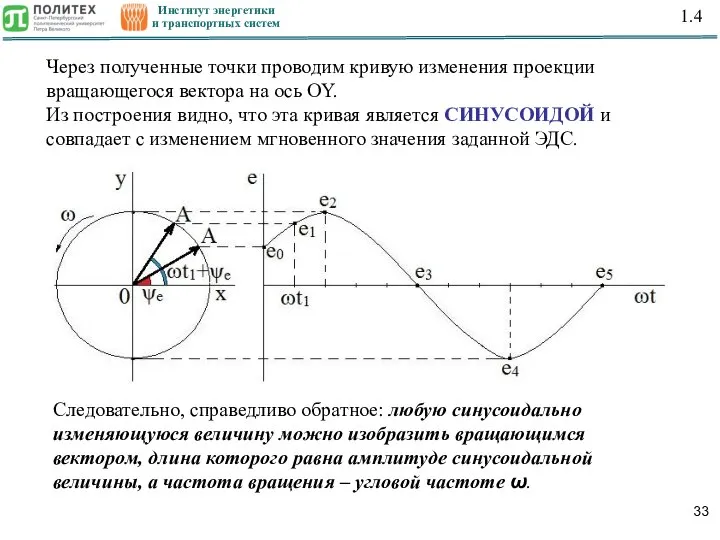
Институт энергетики
и транспортных систем
1.4
Через полученные точки проводим кривую изменения проекции вращающегося вектора на ось OY.
Из построения видно, что эта кривая является СИНУСОИДОЙ и совпадает с изменением мгновенного значения заданной ЭДС.
Следовательно, справедливо обратное: любую синусоидально изменяющуюся величину можно изобразить вращающимся вектором, длина которого равна амплитуде синусоидальной величины, а частота вращения – угловой частоте ω.

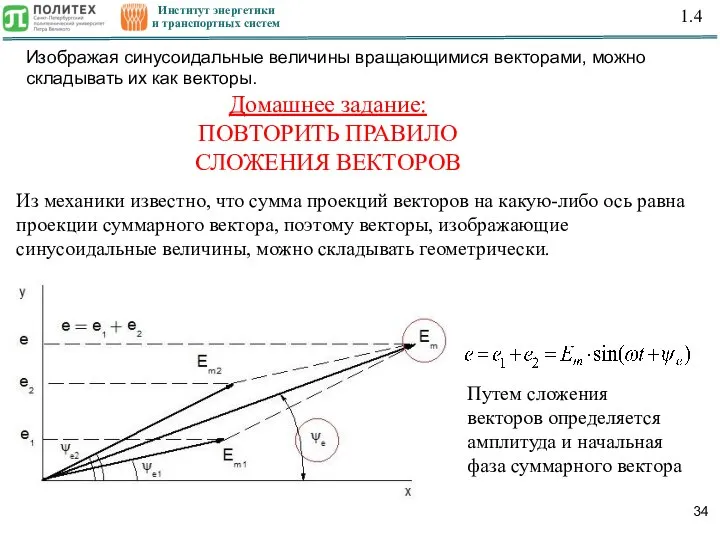
Институт энергетики
и транспортных систем
1.4
Изображая синусоидальные величины вращающимися векторами, можно складывать их как векторы.
Домашнее задание: ПОВТОРИТЬ ПРАВИЛО СЛОЖЕНИЯ ВЕКТОРОВ
Из механики известно, что сумма проекций векторов на какую-либо ось равна проекции суммарного вектора, поэтому векторы, изображающие синусоидальные величины, можно складывать геометрически.
Путем сложения векторов определяется амплитуда и начальная фаза суммарного вектора

Институт энергетики
и транспортных систем
1.4
ВАЖНО: Векторами можно изображать действующие значения синусоидальных величин, но вращать эти вектора нельзя, т.к. их проекции на ось OY ничего не изображают.
Векторная диаграмма
ПРАВИЛО: При построении векторной диаграммы один из векторов принимают за начальный и проводят его в любом удобном направлении (по горизонтали или вертикали). Остальные векторы ориентируют относительно начального.
ПРАВИЛО: Положительное вращение векторов принято против часовой стрелки, поэтому вектор I отстает от вектора U, угол между векторами ─ сдвиг фаз φ.
φ = ψu ─ ψi

Институт энергетики
и транспортных систем
1.1-1.4
Выводы:
Любую синусоидальную величину можно изобразить вектором.
На векторной диаграмме можно изобразить векторы только тех синусоидальных величин, которые изменяются с одинаковой частотой.
Синусоидальные величины изображаются векторами. Это временные векторы, а не пространственные.