Содержание
- 2. Введение определённого интеграла
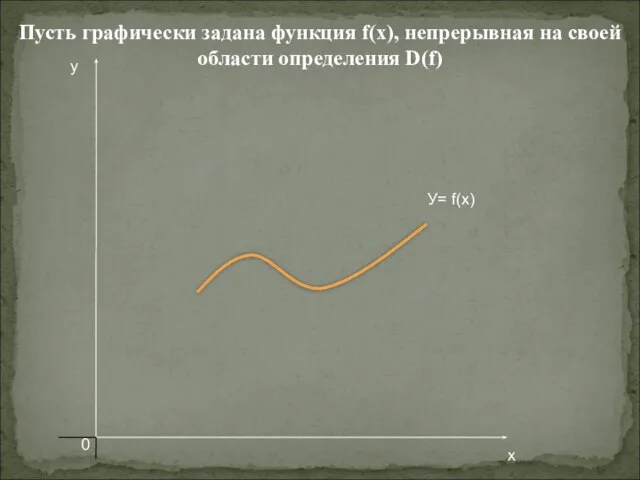
- 3. Пусть графически задана функция f(x), непрерывная на своей области определения D(f) y
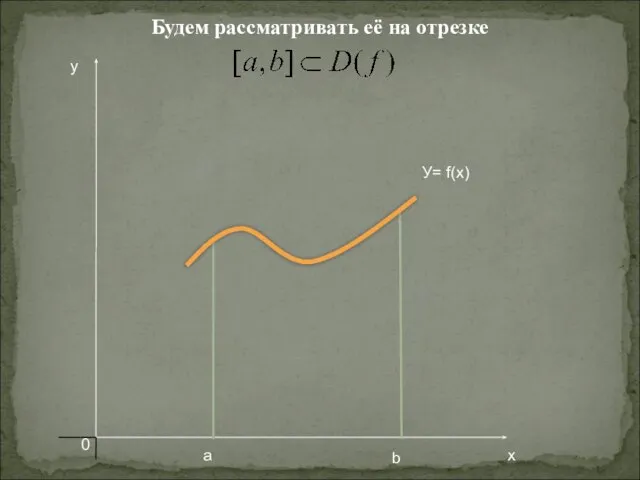
- 4. Будем рассматривать её на отрезке y а b
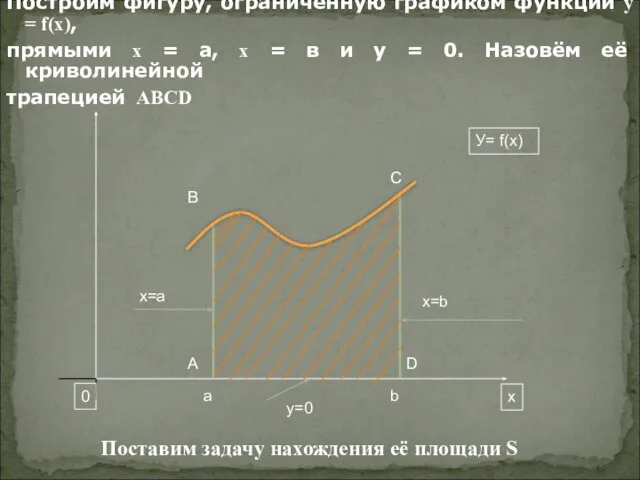
- 5. Построим фигуру, ограниченную графиком функции y = f(x), прямыми x = а, x = в и
- 6. Разделим основание [АD] трапеции ABCD точками х0=а;х1;х2;…; хn= b (x0= a Через точки деления проведём прямые
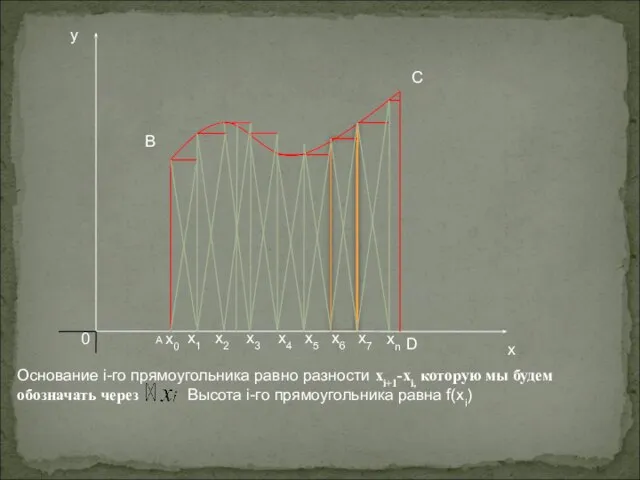
- 7. Каждой полосе поставим в соответствие прямоугольник, одна сторона которого есть отрезок [xi;xi+1], а смежная сторона –
- 8. Основание i-го прямоугольника равно разности xi+1-хi, которую мы будем обозначать через Высота i-го прямоугольника равна f(xi)
- 9. Площадь i-го прямоугольника равна: Сложив площади всех прямоугольников, получаем приближенное значение площади S криволинейной трапеции:
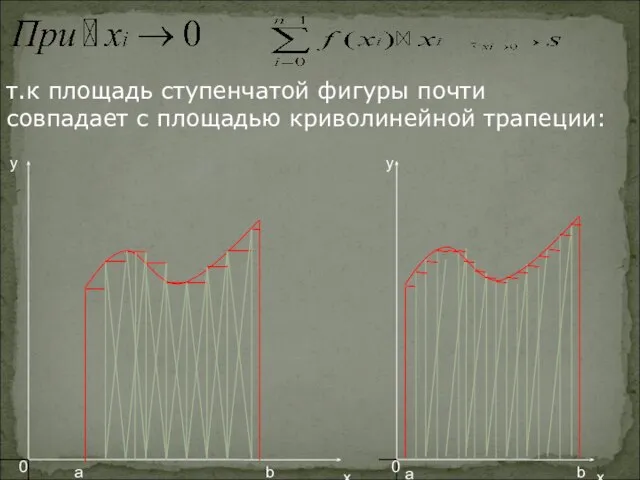
- 10. т.к площадь ступенчатой фигуры почти совпадает с площадью криволинейной трапеции: y a b y a b
- 11. Точное значение площади S получается как предел суммы площадей всех прямоугольников Для обозначения предельных сумм вида
- 12. Если предел функции f(x) существует, то f(x) называется интегрируемой на отрезке [a,b]. Числа а и b
- 13. Некоторые приложения определённого интеграла
- 14. Задача Вычислить площадь фигуры F, ограниченной линиями y= 4-x2 и y= x2-2x 1) Площадь плоской фигуры
- 15. Построим фигуру F. Для этого построим линии, ограничивающие эту фигуру Решим задачу по следующему алгоритму: D
- 16. Найдем точки пересечения этих парабол A(-1;3); B(2;0) Искомую площадь Sf можно найти как алгебраическую сумму площадей
- 18. 2) Объем тела вращения Пусть тело образуется при вращении вокруг оси OX криволинейной трапеции x1ABx2 Любое
- 19. ЗАДАЧА Вычислить объем шара, получаемого вращением полуокружности вокруг оси OX Построим полуокружность y X R -R
- 21. Скачать презентацию

![Разделим основание [АD] трапеции ABCD точками х0=а;х1;х2;…; хn= b (x0= a Через](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/349641/slide-5.jpg)
![Каждой полосе поставим в соответствие прямоугольник, одна сторона которого есть отрезок [xi;xi+1],](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/349641/slide-6.jpg)


![Если предел функции f(x) существует, то f(x) называется интегрируемой на отрезке [a,b].](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/349641/slide-11.jpg)




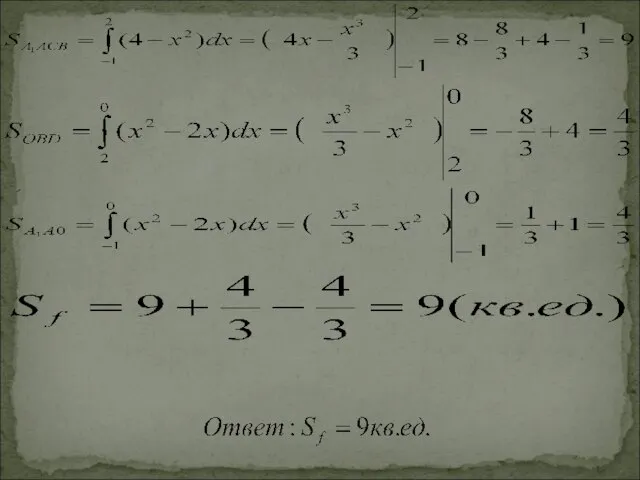


 Время и календарь
Время и календарь Методические рекомендации по организации портфолио по курсу «Юридическая психология»
Методические рекомендации по организации портфолио по курсу «Юридическая психология» Яркие представители мира динозавров
Яркие представители мира динозавров Тип кольчатые черви 7 класс
Тип кольчатые черви 7 класс Дизайн и реклама – составляющие художественной культуры
Дизайн и реклама – составляющие художественной культуры Рождение капитализма (новый общественный строй)
Рождение капитализма (новый общественный строй) Сущность и принципы маркетинга
Сущность и принципы маркетинга Древние мифы, легенды, сказки, предания, благожеланиея дальневосточной земли.
Древние мифы, легенды, сказки, предания, благожеланиея дальневосточной земли. Всероссийский День правовой помощи детям. Права человека
Всероссийский День правовой помощи детям. Права человека Талант помогает исправиться
Талант помогает исправиться Зинин
Зинин Urok_11
Urok_11 Политическое поведение
Политическое поведение Спорт в Британии
Спорт в Британии Таможенное оформление круизных лайнеров и их пассажиров
Таможенное оформление круизных лайнеров и их пассажиров «Построение маркетинговых коммуникаций с молодёжной аудиторией в соответствии с её образом жизни и моделью потребления»
«Построение маркетинговых коммуникаций с молодёжной аудиторией в соответствии с её образом жизни и моделью потребления» Виды Дверей
Виды Дверей Рецепция римского права
Рецепция римского права 幅作品. 戴花的惠安阿婆
幅作品. 戴花的惠安阿婆 Основы научных исследований и инновационной деятельности
Основы научных исследований и инновационной деятельности “Fried Green Tomatoes at the Whistle Stop Café”
“Fried Green Tomatoes at the Whistle Stop Café” Синяя лента апреля
Синяя лента апреля Формы и системы оплаты труда на предприятиях
Формы и системы оплаты труда на предприятиях КАК ОРГАНИЗОВАТЬ КОНКУРС КИО В ШКОЛЕ
КАК ОРГАНИЗОВАТЬ КОНКУРС КИО В ШКОЛЕ Числа с собственными именами
Числа с собственными именами Послеоперационный период
Послеоперационный период  Программа amoCRM
Программа amoCRM Реализация PR и IR стратегий: особенности национального информационного поля
Реализация PR и IR стратегий: особенности национального информационного поля