Слайд 2Опт. планирование
Это определение значений плановых показателей с учетом ограниченности ресурсов при условии

достижения заданной цели
Слайд 3ЗАДАЧА
Школьный кондитерский цех готовит пирожки и пирожные. В силу ограниченности условий можно

приготовить не более 700 штук изделий. Рабочий день длится 8 часов. За день можно произвести не более 250 пирожных, пирожков – 1000 (по отдельности).
Стоимость пирожного вдвое выше стоимости пирожка. Требуется составить такой дневной план производства, чтобы обеспечить наибольшую выручку.
Слайд 4Математическая модель
X – пирожков
У- пирожных
Длительность рабочего дня – 8 часов
Склад – на

700 мест
t - время на 1 пирожок
4t – на 1 пирожное
tx+4ty = (x+4y)t
(x+4y)t <=8*60
(x+4y)t <=480
480/1000 = 0,48 мин – на 1 пирожок
Слайд 5Математическая модель
(x+4y)t <=480
t = 0,48
(x+4y)0,48 <=480
X+4y<=1000
Получим систему условий:
х+4y<=1000
x+y<=700 –

общее кол-во
X>=0
Y>=0
Слайд 6Стратегическая цель
Требуется найти значения х и у, удовлетворяющих системе неравенств и

придающих максимальное значение целевой функции
Получение максимальной выручки!
r- цена 1 пирожка
2r- цена 1 пирожного
rx +2ry = r(x+2y) – целевая функция
r=const, x+2y = max





 Животные. Брачные обряды
Животные. Брачные обряды Клинический случай. Корь у привитого ребенка 1,6 лет с неустановленным контактом
Клинический случай. Корь у привитого ребенка 1,6 лет с неустановленным контактом Обучение иностранным языкам в современной информационно- образовательной среде
Обучение иностранным языкам в современной информационно- образовательной среде 30 апреля – 5 мая 2012 года
30 апреля – 5 мая 2012 года Презентация на тему Япония 7 класс
Презентация на тему Япония 7 класс Требуются рабочие ООО РосПромПерсонал
Требуются рабочие ООО РосПромПерсонал Презентация на тему файлы и папки 6 класс презентация
Презентация на тему файлы и папки 6 класс презентация  Принцесса Рапунцель
Принцесса Рапунцель Презентация на тему Конституционные обязанности человека и гражданина
Презентация на тему Конституционные обязанности человека и гражданина Шумоанализация или Как шум влияет на здоровье и внимание школьника
Шумоанализация или Как шум влияет на здоровье и внимание школьника Главные типы почв России
Главные типы почв России СИСТЕМА МЕНЕДЖМЕНТА КАЧЕСТВА в СГТА
СИСТЕМА МЕНЕДЖМЕНТА КАЧЕСТВА в СГТА Политология. Лекция 3.1
Политология. Лекция 3.1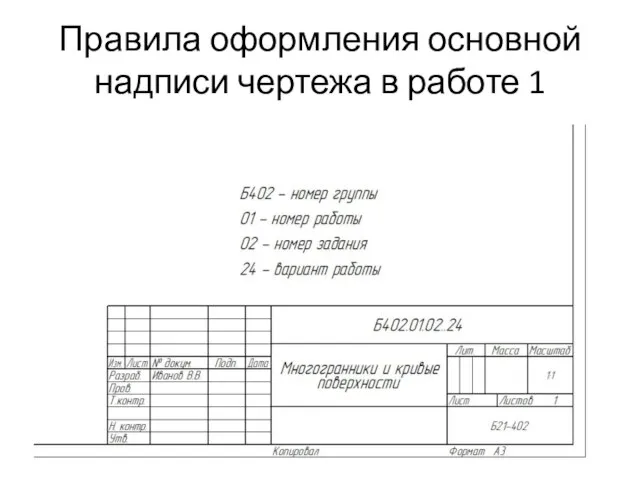 Правила оформления основной надписи чертежа в работе 1
Правила оформления основной надписи чертежа в работе 1 ООО «ЭкоЛайф 69»
ООО «ЭкоЛайф 69» Презентация на тему Информация и цивилизация
Презентация на тему Информация и цивилизация Étude deefine
Étude deefine Лекция 3 - Вывод уравнений узловых напряжений
Лекция 3 - Вывод уравнений узловых напряжений Система оценка качества образования в Забайкальском крае
Система оценка качества образования в Забайкальском крае Волшебный мир
Волшебный мир Внешняя политика СССР в 1930-е гг. и накануне Великой Отечественной войны
Внешняя политика СССР в 1930-е гг. и накануне Великой Отечественной войны Введение компетентностного подхода в современное образование
Введение компетентностного подхода в современное образование Ama Kids, рейтинг
Ama Kids, рейтинг Ресинхронизирующая терапия при ХСНMеханизмы, клиничексие аспекты, выбор пациента, имплантация
Ресинхронизирующая терапия при ХСНMеханизмы, клиничексие аспекты, выбор пациента, имплантация Исследовательская деятельность
Исследовательская деятельность OS definition
OS definition Физические явления
Физические явления Сценарнорежиссерские основы культурно-досуговых программ
Сценарнорежиссерские основы культурно-досуговых программ