Слайд 2Классификация прямых
Прямые общего положения – это прямые, непараллельные и неперпендикулярные ни

одной из плоскостей проекций.
Прямые частного положения:
Уровня – параллельные одной из плоскостей проекций и не перпендикулярные двум другим;
Проецирующие – перпендикулярные к одной плоскости проекций и параллельные двум другим.
Слайд 3Позиционно-метрические свойства прямой:
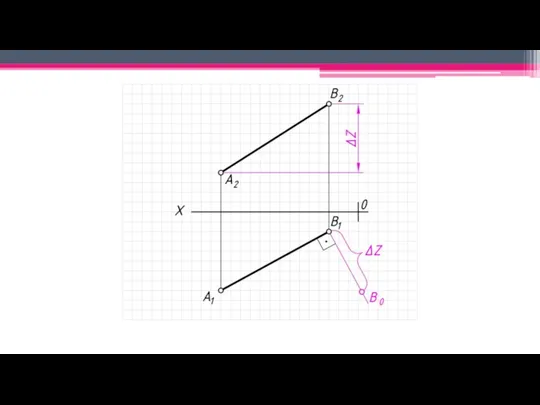
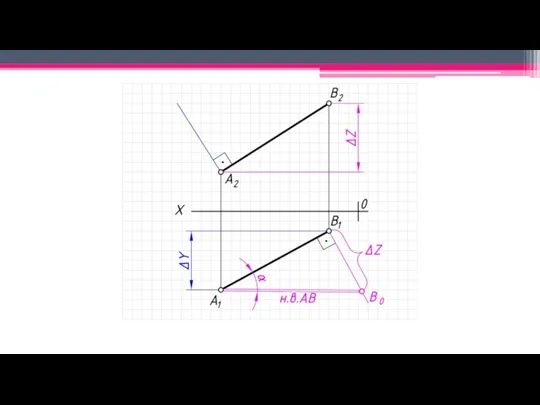
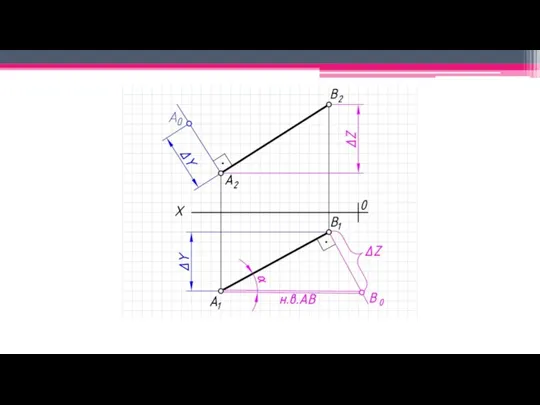
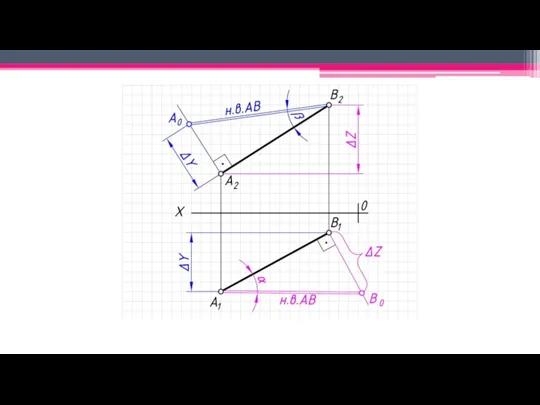
Натуральная величина прямой – определяется способом прямоугольного треугольника.
Угол наклона отрезка

прямой к соответствующей плоскости проекций является угол между его проекцией на данную плоскость и натуральной величиной рассматриваемого отрезка.
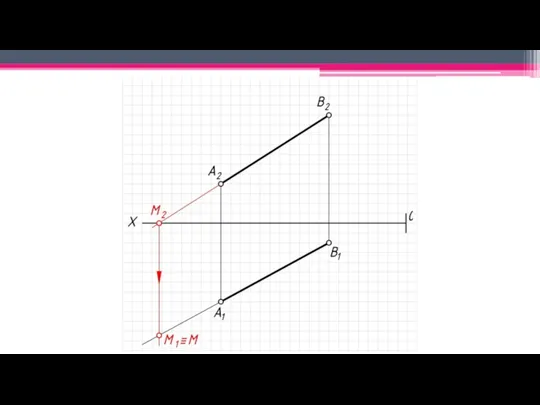
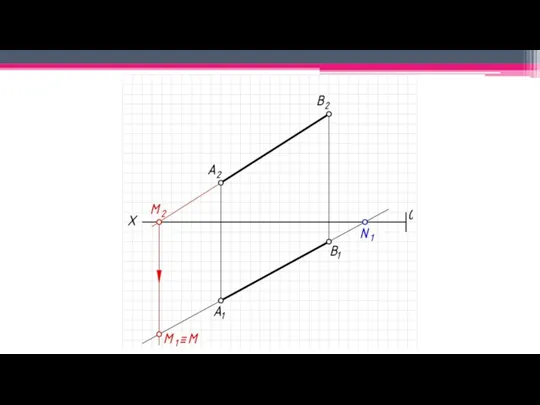
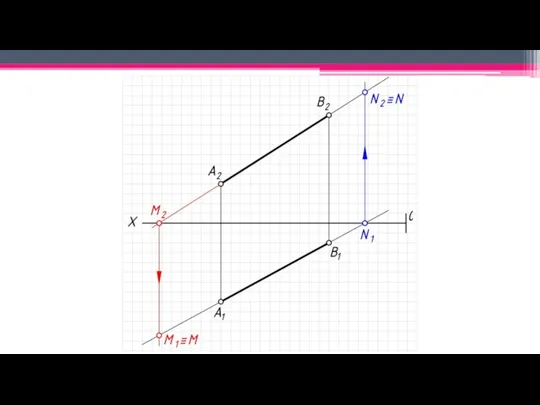
Слайд 11След прямой – точка пересечения прямой с плоскостью проекций
(N – фронтальный
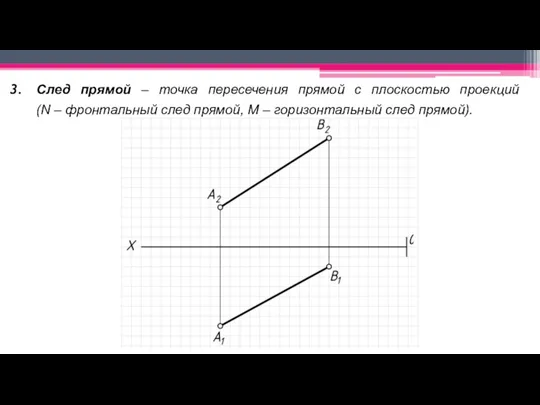
след прямой, M – горизонтальный след прямой).
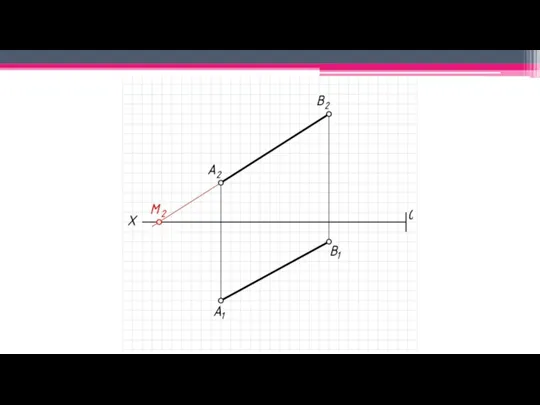
Слайд 16Принадлежность точки прямой.
Теорема: Если в пространстве точка принадлежит прямой, то на чертеже

одноименные проекции точки принадлежат одноименным проекциям прямой.
Теорема: Если в пространстве точка делит отрезок прямой в каком-то отношении, то на чертеже проекции этой точки делят одноименные проекции отрезка в том же отношении.
Слайд 17Принадлежность точки прямой.
Теорема: Если в пространстве точка принадлежит прямой, то на чертеже

одноименные проекции точки принадлежат одноименным проекциям прямой.
Теорема: Если в пространстве точка делит отрезок прямой в каком-то отношении, то на чертеже проекции этой точки делят одноименные проекции отрезка в том же отношении.
Слайд 18ПРЯМЫЕ УРОВНЯ:
Прямая горизонтального
уровня (12 // П1).
1222 // OX и 1323 // OY,
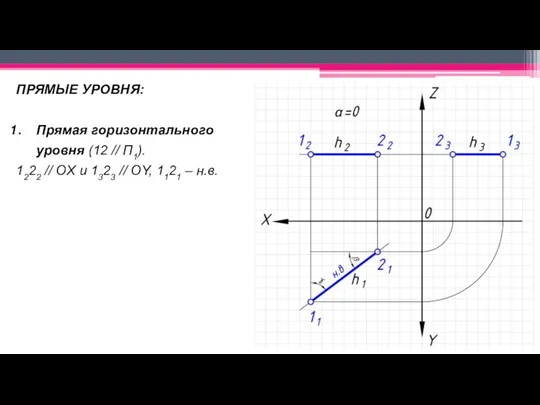
1121 – н.в.
Слайд 19Прямая фронтального
уровня (12 // П2).
1121 // OX и 1323 // OZ, 1222
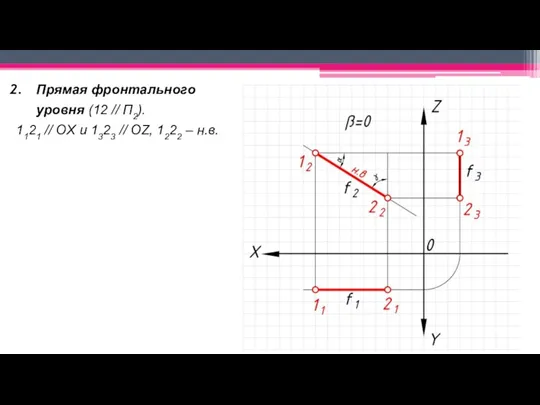
– н.в.
Слайд 20Прямая профильного
уровня (12 // П3).
1121 // OY и 1222 // OZ, 1323
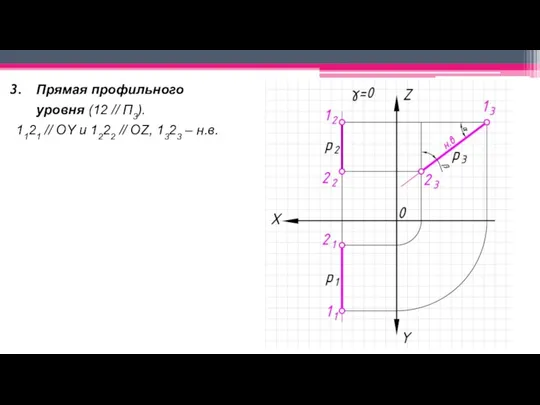
– н.в.
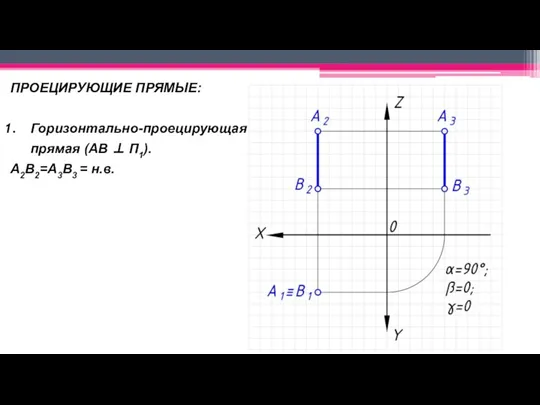
Слайд 21ПРОЕЦИРУЮЩИЕ ПРЯМЫЕ:
Горизонтально-проецирующая прямая (АВ ⊥ П1).
A2B2=A3B3 = н.в.
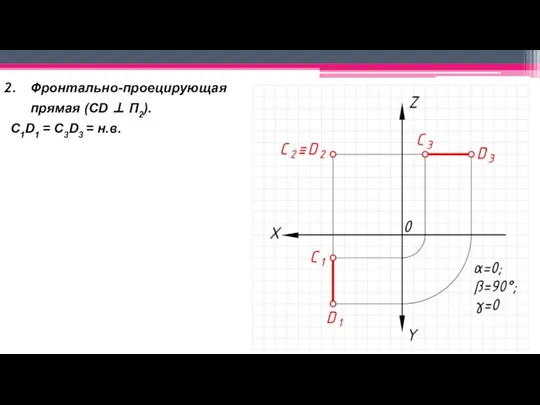
Слайд 22Фронтально-проецирующая прямая (CD ⊥ П2).
С1D1 = C3D3 = н.в.
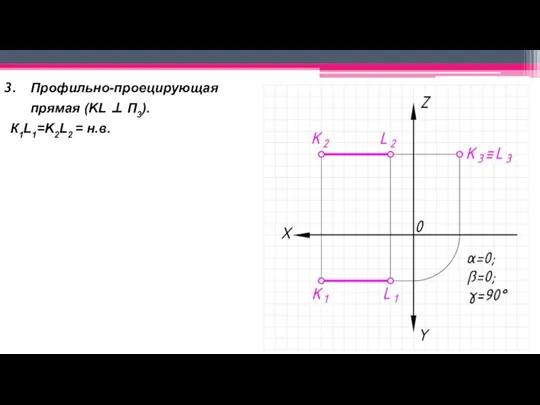
Слайд 23Профильно-проецирующая прямая (KL ⊥ П3).
К1L1=K2L2 = н.в.
Слайд 24ВЗАИМНОЕ ПОЛОЖЕНИЕ ПРЯМЫХ
Параллельные прямые – прямые, принадлежащие одной плоскости и не имеющие
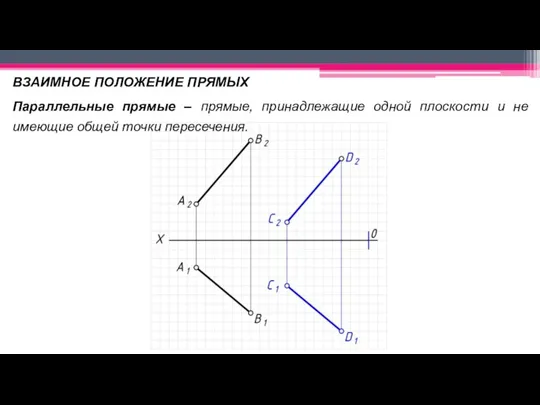
общей точки пересечения.
Слайд 25Пересекающиеся прямые – прямые, принадлежащие одной плоскости и имеющие одну общую точку
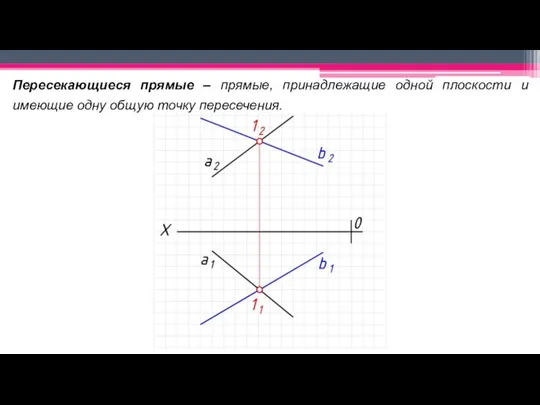
пересечения.
Слайд 26Скрещивающиеся прямые – прямые, не принадлежащие одной плоскости и не имеющие общих
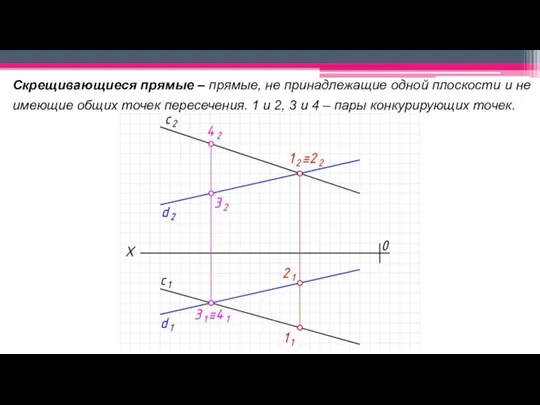
точек пересечения. 1 и 2, 3 и 4 – пары конкурирующих точек.


















 КАБИНЕТФАКТОЛОГИИ И АНАЛИЗА ДАННЫХ ПО ПРЕДВИДЕНИЮ(www.chronos.msu.ru/cabinets/predvidenie)С.А.Кравченко (www.skravchenko.ru)Москва30 ноября 2010 г.
КАБИНЕТФАКТОЛОГИИ И АНАЛИЗА ДАННЫХ ПО ПРЕДВИДЕНИЮ(www.chronos.msu.ru/cabinets/predvidenie)С.А.Кравченко (www.skravchenko.ru)Москва30 ноября 2010 г. Значение нейронаук для специальной педагогики и психологии
Значение нейронаук для специальной педагогики и психологии Фотографии
Фотографии Антивирусы TrustPort
Антивирусы TrustPort ВПК
ВПК florists department
florists department Основные теги HTML
Основные теги HTML Презентация на тему НАСЕЛЕНИЕ ЗЕМЛИ
Презентация на тему НАСЕЛЕНИЕ ЗЕМЛИ  Формирование толерантности у школьников
Формирование толерантности у школьников Терапевтическая локализация
Терапевтическая локализация  Города-Герои
Города-Герои Бесконтактный велогенератор
Бесконтактный велогенератор Тема 7 (2)
Тема 7 (2) Безграничное пространство сцены
Безграничное пространство сцены Тест на развития когнитивных функций головного мозга. Анаграммы
Тест на развития когнитивных функций головного мозга. Анаграммы Ресурсный центр ядерной медицины СПбГУ Перспективы развития исследований в области медицины и биологии
Ресурсный центр ядерной медицины СПбГУ Перспективы развития исследований в области медицины и биологии УРОВНИ ОРГАНИЗАЦИИ ЖИЗНИНА ЗЕМЛЕ
УРОВНИ ОРГАНИЗАЦИИ ЖИЗНИНА ЗЕМЛЕ Artrologia
Artrologia 23 февраля
23 февраля Горецкий В.Г. Азбука. Учебник: 1 класс: В 2ч Горецкий В.Г., Федосова Н.А, Прописи к "Русской азбуке" 1,2,3,4.
Горецкий В.Г. Азбука. Учебник: 1 класс: В 2ч Горецкий В.Г., Федосова Н.А, Прописи к "Русской азбуке" 1,2,3,4. Силы. Сила тяжести
Силы. Сила тяжести "Жизнь или никотин"
"Жизнь или никотин" Страна фараонов Египет
Страна фараонов Египет Системы урегулирования убытка и контроля расчетов страхового возмещения центральными офисами страховых компаний.
Системы урегулирования убытка и контроля расчетов страхового возмещения центральными офисами страховых компаний. Формирование межкультурной компетенции обучающихся в процессе анализа текстов современных англоязычных СМИ
Формирование межкультурной компетенции обучающихся в процессе анализа текстов современных англоязычных СМИ КВН
КВН Самоконтроль в процессе занятий физкультурой и спортом. Пульс (занятие 9)
Самоконтроль в процессе занятий физкультурой и спортом. Пульс (занятие 9) Предзаказы на 8 марта. Шашлычная
Предзаказы на 8 марта. Шашлычная