Содержание
- 2. СОДЕРЖАНИЕ ВВЕДЕНИЕ 1. МЕТОД ПРОДОЛЖЕНИЯ ПО ПАРАМЕТРУ 2. ОПТИМАЛЬНЫЕ МЕЖПЛАНЕТНЫЕ ПЕРЕЛЕТЫ КА С ИДЕАЛЬНО РЕГУЛИРУЕМЫМ ДВИГАТЕЛЕМ
- 3. ВВЕДЕНИЕ Представлен единый методический подход к решению различных задач численной оптимизации траекторий КА с малой тягой.
- 4. Оптимизация перелетов КА с малой тягой: Т.М. Энеев, В.А. Егоров, В.В. Белецкий, Г.Б. Ефимов, М.С. Константинов,
- 5. Недостатки традиционных численных методов оптимизации малая область сходимости; вычислительная неустойчивость; необходимость подбора начального приближения в условиях
- 6. Цель разработки метода продолжения “Регуляризация” численной оптимизации траекторий, то есть устранение, по возможности, методических недостатков численной
- 7. 7
- 8. 8
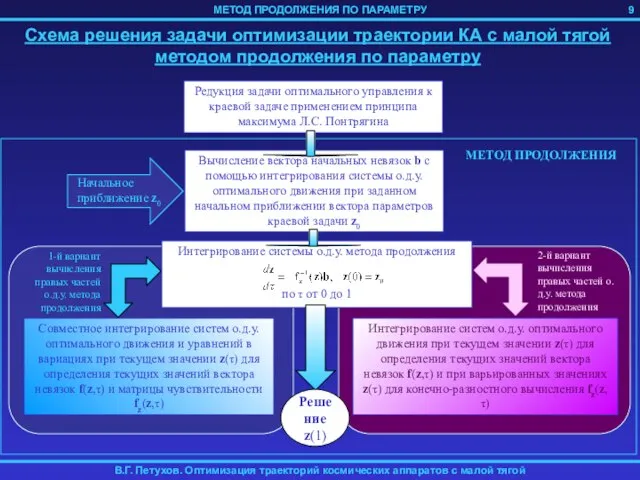
- 9. 9
- 10. 2. ОПТИМАЛЬНЫЕ МЕЖПЛАНЕТНЫЕ ПЕРЕЛЕТЫ КА С ИДЕАЛЬНО РЕГУЛИРУЕМЫМ ДВИГАТЕЛЕМ МАЛОЙ ТЯГИ 10
- 11. 11
- 12. 2.2. УРАВНЕНИЯ ОПТИМАЛЬНОГО ДВИЖЕНИЯ (СЛУЧАЙ ПОСТОЯННОЙ МОЩНОСТИ) 12
- 13. 13
- 14. 14
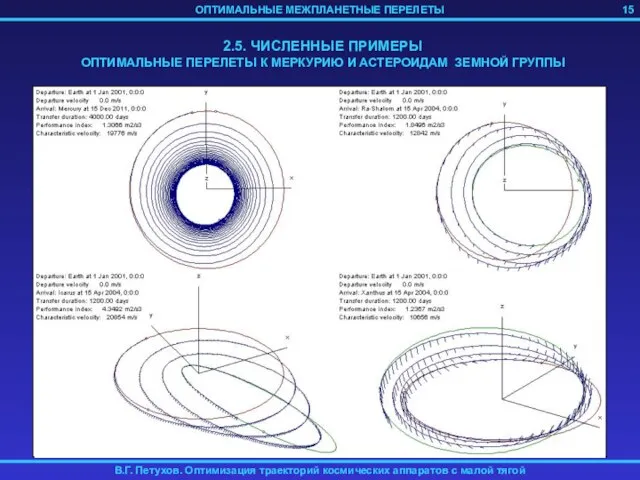
- 15. 15
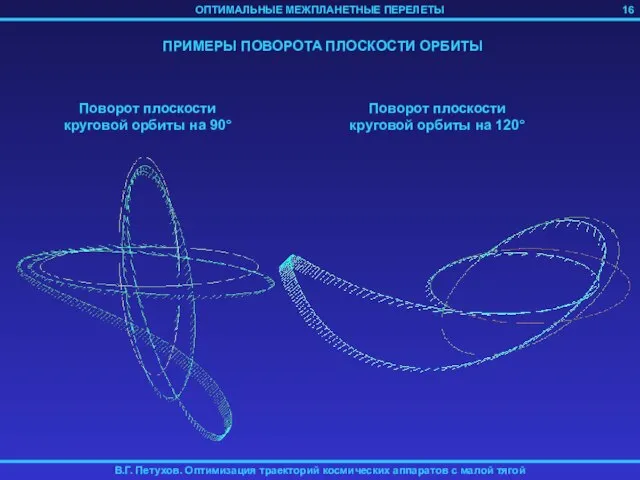
- 16. 16
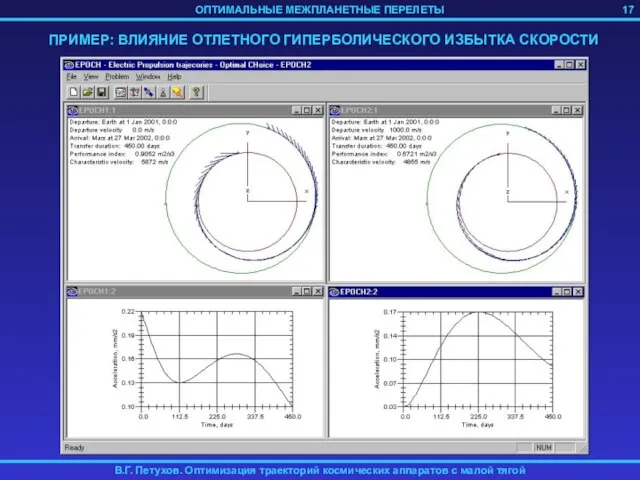
- 17. ПРИМЕР: ВЛИЯНИЕ ОТЛЕТНОГО ГИПЕРБОЛИЧЕСКОГО ИЗБЫТКА СКОРОСТИ 17
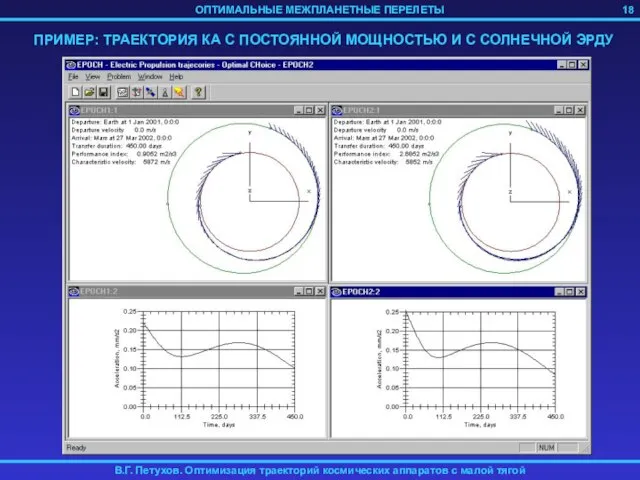
- 18. ПРИМЕР: ТРАЕКТОРИЯ КА С ПОСТОЯННОЙ МОЩНОСТЬЮ И С СОЛНЕЧНОЙ ЭРДУ 18
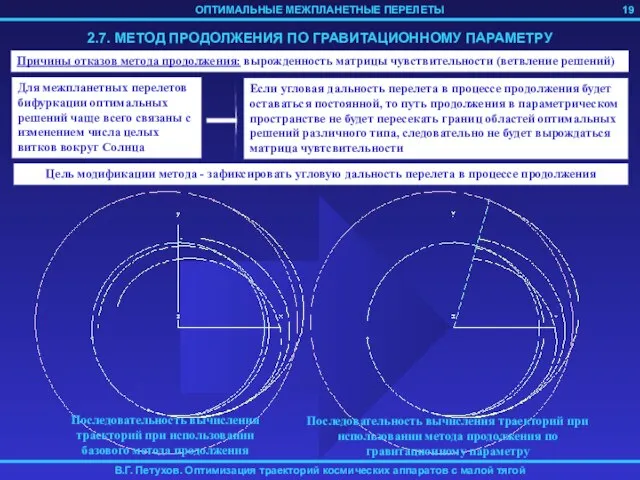
- 19. 19
- 20. 20
- 21. 21
- 22. 22
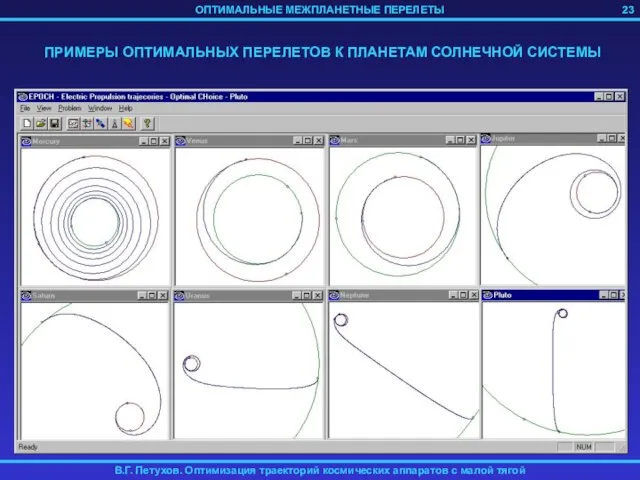
- 23. ПРИМЕРЫ ОПТИМАЛЬНЫХ ПЕРЕЛЕТОВ К ПЛАНЕТАМ СОЛНЕЧНОЙ СИСТЕМЫ 23
- 24. 3. ОПТИМИЗАЦИЯ ТРАЕКТОРИИ ПЕРЕЛЕТА НА ОРБИТУ ВОКРУГ ЛУНЫ КА С ИДЕАЛЬНО РЕГУЛИРУЕМЫМ ДВИГАТЕЛЕМ МАЛОЙ ТЯГИ Рассматривается
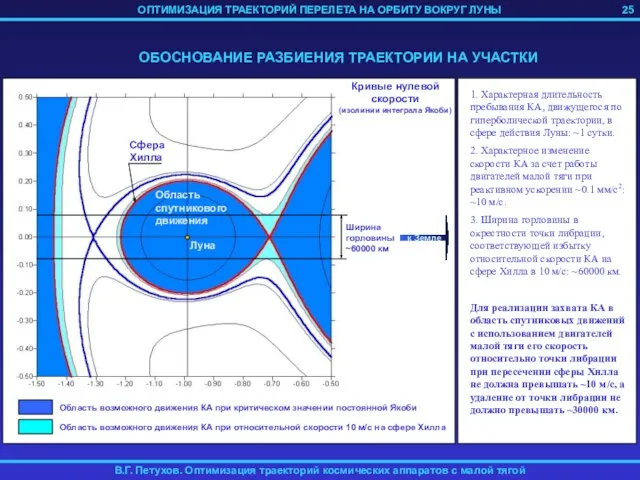
- 25. 25
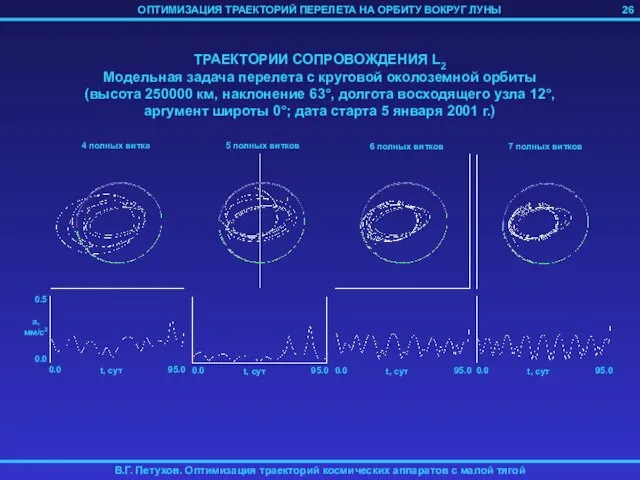
- 26. 26
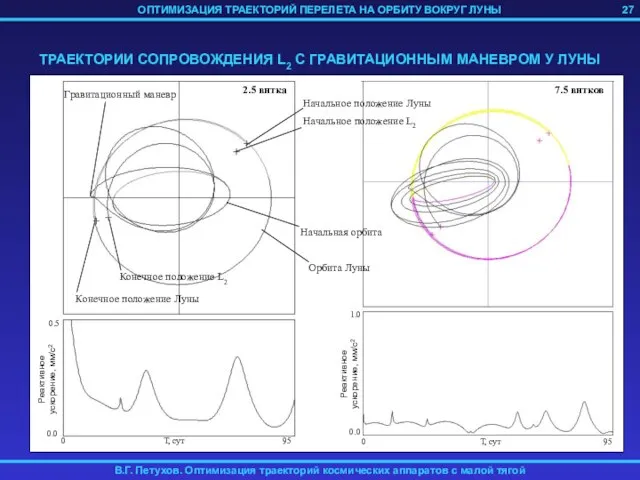
- 27. 27
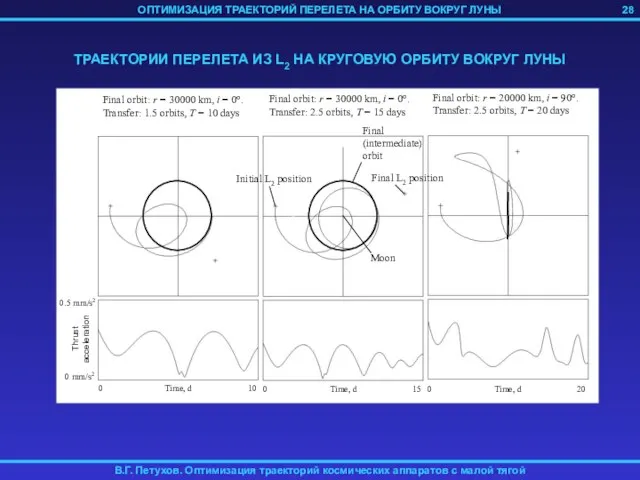
- 28. 28
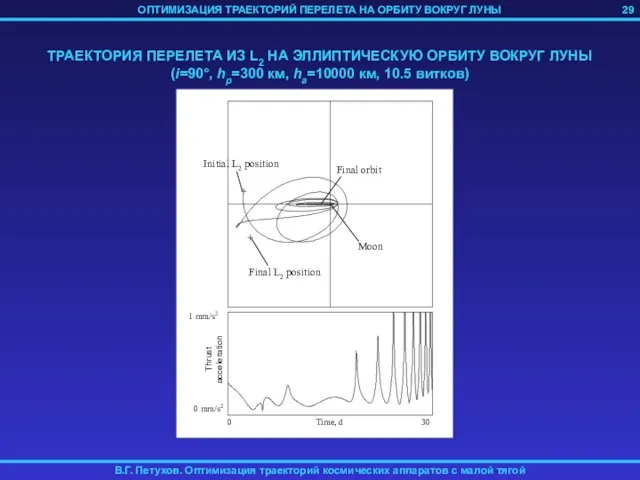
- 29. 29
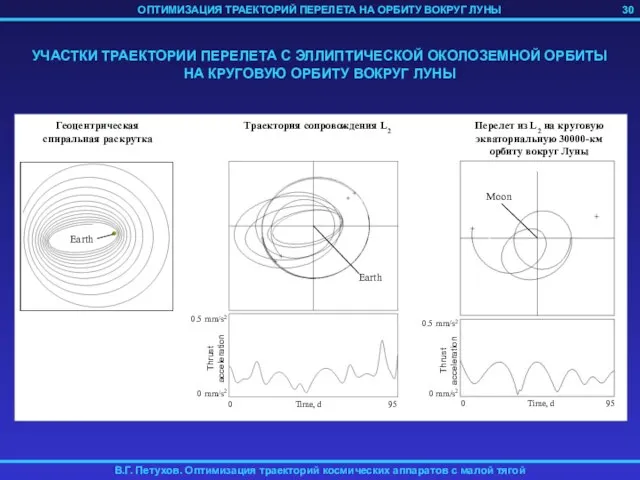
- 30. 30
- 31. 4. ОПТИМИЗАЦИЯ МНОГОВИТКОВЫХ ПЕРЕЛЕТОВ МЕЖДУ НЕКОМПЛАНАРНЫМИ ЭЛЛИПТИЧЕСКИМИ ОРБИТАМИ 31
- 32. Уравнения орбитального движения КА записываются в равноденственных элементах, не имеющих особенностей при нулевом наклонении и эксцентриситете.
- 33. 33
- 34. 34
- 35. 35
- 36. 36
- 37. 37
- 38. 4.5. ОСОБЕННОСТИ РЕШЕНИЯ КРАЕВОЙ ЗАДАЧИ Краевая задача решается методом продолжения по параметру. Для вычисления невязок f
- 39. 4.6. ОПТИМАЛЬНОЕ РЕШЕНИЕ В НЕОСРЕДНЕННОМ ДВИЖЕНИИ Малый уровень реактивного ускорения (по сравнению с гравитационным) обуславливает близость
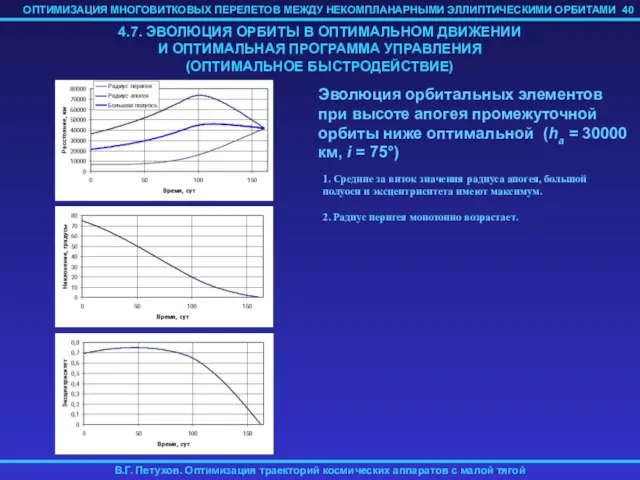
- 40. 40
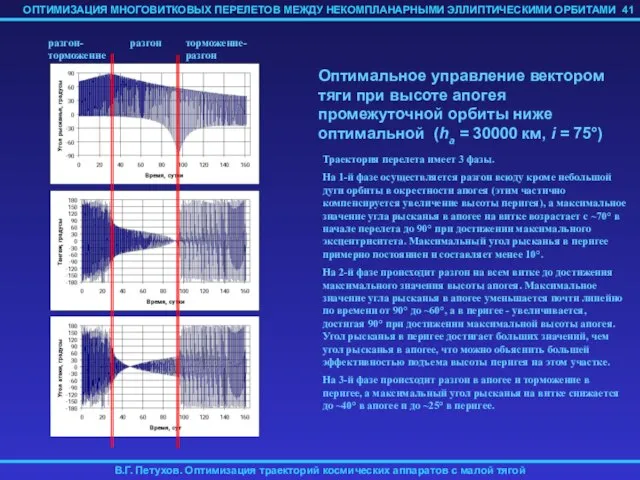
- 41. 41
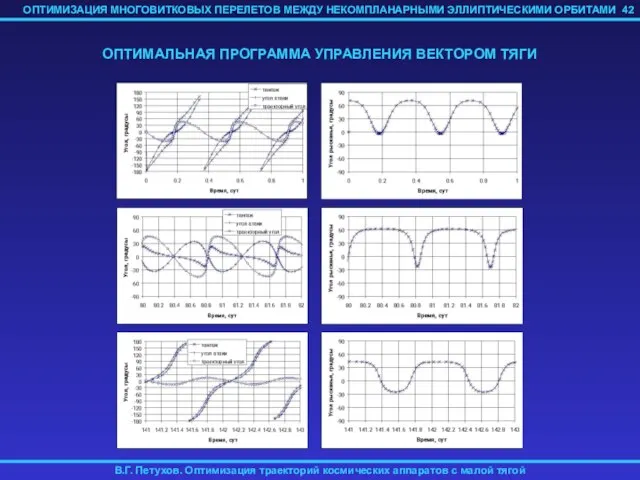
- 42. 42
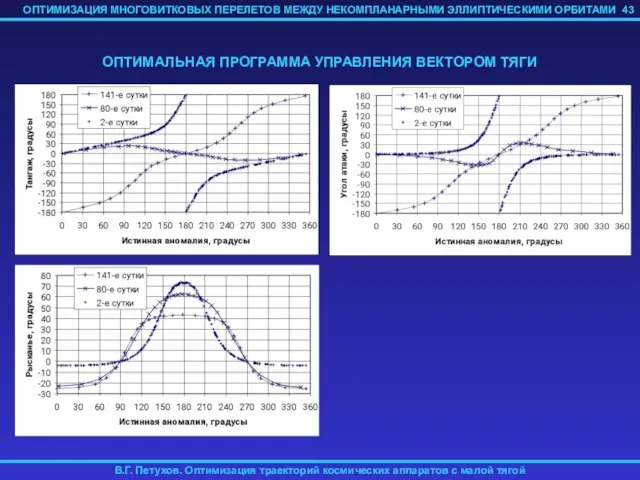
- 43. 43
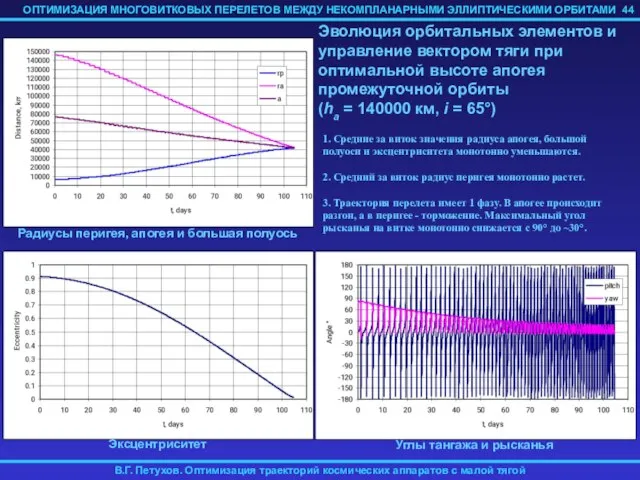
- 44. 44
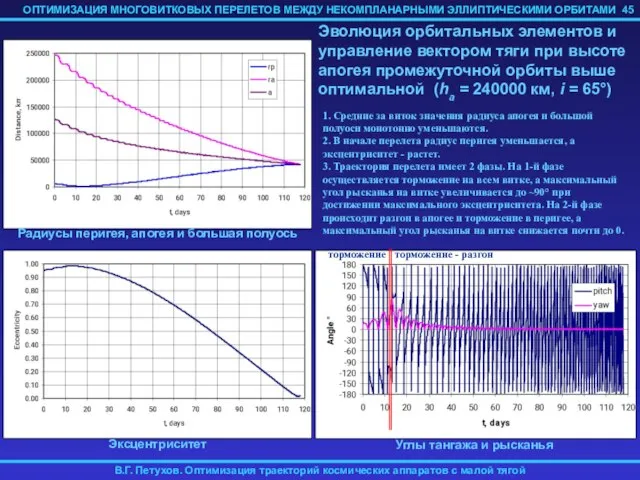
- 45. 45
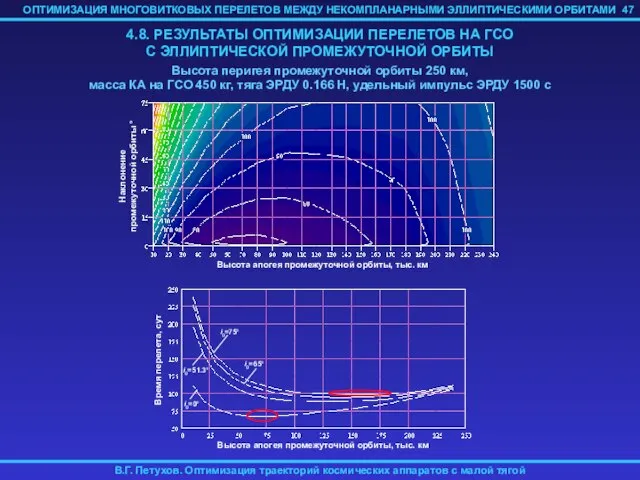
- 47. 47
- 48. 4.9. ВЫВОДЫ 1. Метод продолжения по параметру можно эффективно использовать для оптимизации многовитковых перелетов с малой
- 50. Скачать презентацию



























 آموزش سواد رسانه ای – درس سوم
آموزش سواد رسانه ای – درس سوم Раскрытие скобок. Линейные уравнения. Повторение
Раскрытие скобок. Линейные уравнения. Повторение История Древнего Рима (МХК 10 класс)
История Древнего Рима (МХК 10 класс) МОДУЛЬНАЯ
МОДУЛЬНАЯ Лучшие инструменты для сведения звука (саундпродюссинг)
Лучшие инструменты для сведения звука (саундпродюссинг) Деловые документы (автобиография, заявление, резюме )
Деловые документы (автобиография, заявление, резюме ) MixMarket.BIZ
MixMarket.BIZ Практика-Инфекции-3 (Бактериальные)
Практика-Инфекции-3 (Бактериальные) природные условия
природные условия Презентация на тему Правописание сочетаний Чк чн
Презентация на тему Правописание сочетаний Чк чн Реконструкция системы водоснабжения п. Гирей, Краснодарского края
Реконструкция системы водоснабжения п. Гирей, Краснодарского края Правила проведения банных процедур
Правила проведения банных процедур Лексические нормы
Лексические нормы Организация общения дошкольников в повседневной жизни и разнообразных видах деятельности
Организация общения дошкольников в повседневной жизни и разнообразных видах деятельности Натюрморт в графике. ИЗО. 6 класс
Натюрморт в графике. ИЗО. 6 класс Каким ты видишь мир?
Каким ты видишь мир? Завоевание Римом Италии 5 класс
Завоевание Римом Италии 5 класс Как продавать продукцию IEK® в розницу: формула успеха
Как продавать продукцию IEK® в розницу: формула успеха Мини-волейбол
Мини-волейбол Подача питательной воды в парогенератор при запроектной аварии
Подача питательной воды в парогенератор при запроектной аварии Мы дарим впечатления, которые хочется хранить всю жизнь!
Мы дарим впечатления, которые хочется хранить всю жизнь! Алгоритм выбора профессии. Занятие 15
Алгоритм выбора профессии. Занятие 15 Crisis del Salitre
Crisis del Salitre The obligation
The obligation  Презентация на тему Что надо знать про жевательную резинку
Презентация на тему Что надо знать про жевательную резинку Анализ сайта Развитие ребёнка
Анализ сайта Развитие ребёнка Производственный комплекс АГАМА
Производственный комплекс АГАМА Современное состояние, перспективы развития общин КМНС. - презентация
Современное состояние, перспективы развития общин КМНС. - презентация