Опыты с равновозможными элементарными событиями

Какие события называются равновозможными?
Равновозможные события имеют равные вероятности.
*

Определение
Вероятность произвольного события равна отношению числа элементарных событий, благоприятствующих этому событию, к общему числу элементарных событий.
Р(А) – вероятность события А
N-число элементарных событий
N(A)- число элементарных событий, благоприятствующие событию А

Упражнение 1
Игральную кость бросают два раза. Найти вероятность события «сумма очков меньше 6».
Решение: А – событие «сумма очков меньше 6».
Нарисовать таблицу выпадения очков при бросании кости дважды

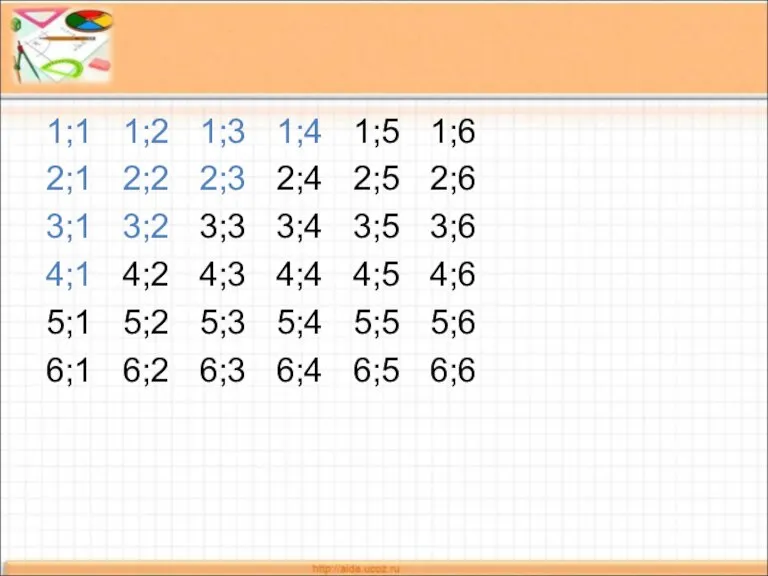
1;1 1;2 1;3 1;4 1;5 1;6
2;1 2;2 2;3 2;4 2;5 2;6
3;1 3;2 3;3 3;4 3;5 3;6
4;1 4;2 4;3 4;4 4;5 4;6
5;1 5;2 5;3 5;4 5;5 5;6
6;1 6;2 6;3 6;4 6;5 6;6

Число событий N=36
Число событий благоприятствующих событию «сумма очков меньше 6»:(1,1)(1,2)(1,3)(1,4) (2,1)(2,2)(2,3)(3,1)(3,2)(4,1)
N(A)=10
Ответ: Р(А)=5\18

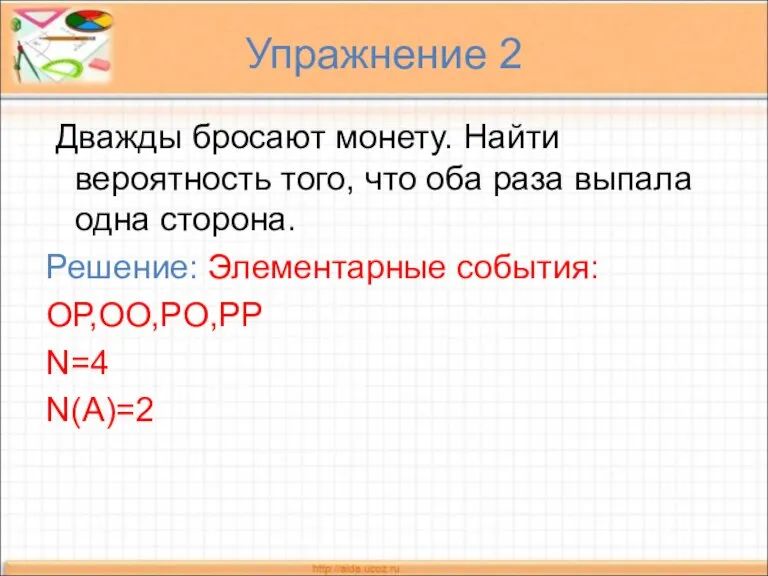
Упражнение 2
Дважды бросают монету. Найти вероятность того, что оба раза выпала одна сторона.
Решение: Элементарные события:
ОР,ОО,РО,РР
N=4
N(A)=2

Ответ: Р(А)=1\2

Упражнение 3
Пятачок идёт из своего дома к дому Винни-Пуха, Винни-Пух идёт из своего дома к дому Пяточка. Каждый из них может выбрать любую дорогу наугад. Найдите вероятность встречи.
Винни-Пух
Пятачок

Решение:
А – событие встречи Пяточка и Винни
Всего элементарных событий
N=4
N(A) =2
Ответ: Р(А)=1\2

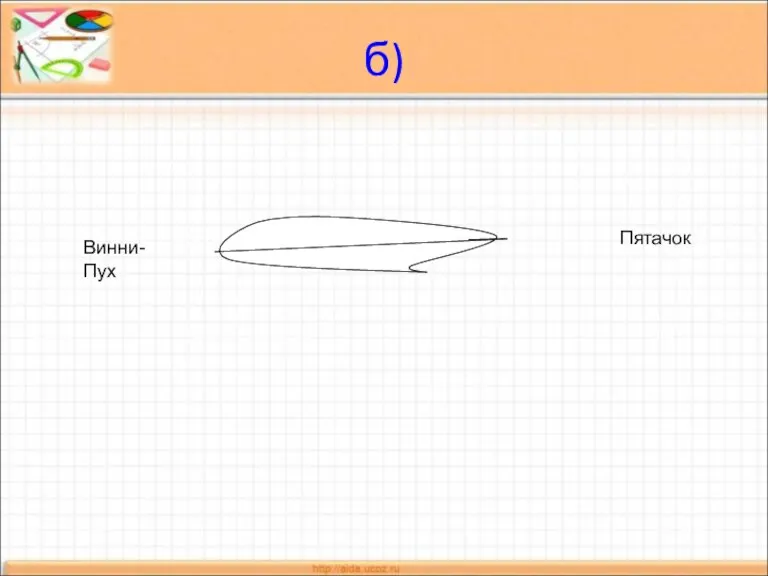
б)
Винни-Пух
Пятачок

Решение:
N=9
N(A)=3
P(A)=1\3

Упражнение 4(Игра «Морской бой»)

а)Найдите вероятность первым же выстрелом попасть в какой-нибудь из кораблей противника.
б) Найдите вероятность первым же выстрелом попасть в четырёхпалубный корабль.
в) Найдите вероятность первым же выстрелом попасть в однопалубный корабль противника

Упражнение 5
При игре в «Морской бой» после первого выстрела противник сообщил, что вы подбили какой-то корабль (но не потопили его). Какова вероятность того, что вы попали :
а)в четырёхпалубный корабль;
б)в трёхпалубный;
в)в двухпалубный?

Упражнение 6(шахматная доска)

Шахматный слон может за один ход перейти на любое число полей, двигаясь только по диагонали. Шахматный слон случайным образом поставлен на доску. Найдите вероятность того, что он может за один ход перейти на поле: а) h1, б) а5, в) с4,
г) d7, д) d5, е) g3.