Основные понятия «Теории вероятностей»

Теория и практика
Люди играют с кубиком, в "орла или решку", во всевозможные лотереи поскольку уверены в том, что эти игры справедливы, т.е. возможный результат каждого события имеет одинаковую вероятность – в противном случае эти игры просто бы не существовали.

Теория и практика
Если подброшенная на ваших глазах реальная монета 100 раз или хотя бы 10 подряд упала "орлом" вверх, то вы можете быть уверены, что она "неправильная", возможно, фальшивая – у нее явно смещен центр тяжести

Математические модели
математическая модель "монета":
выпадение "орла" или "решки "
имеет одинаковую вероятность .
На заре зарождения теории вероятностей были скептики –исследователи, сомневавшиеся в этом вполне очевидном для нас факте и очень много раз подбрасывали монету, но всегда убеждались, что "орел" выпадает в половине случаев.
Статистика

Количество выпадений "орла" при многократном подбрасывания монеты
10 006 раз –
для первых 20 000 бросаний,
9 996 раз–
для вторых 20 000 бросаний,
20 002 раз–
для всех 40 000 бросаний.
В любом случае частота выпадения
"орла" была очень близка к половине.

Математические модели
математическая модель «игральная кость»:
выпадение каждой грани
при многократном бросании кубика
имеет одинаковую вероятность .

События и испытания
Предметом исследования в теории вероятностей являются события, появляющиеся при определенных условиях, которые можно воспроизводить неограниченное количество раз.
Каждое осуществление этих условий называют испытанием
Примеры

Примеры испытаний и событий
Испытание – бросание игральной кости
Событие – выпадение шестерки или выпадение четного числа очков
Испытание – взвешивание тела на аналитических весах
Событие – ошибка измерения не превзойдет заранее заданного числа

Вероятность случайного события
Степень объективной возможности случайного события можно измерять числом.
Это число называется
вероятностью случайного события.
Около этого числа группируются относительные частоты данного случайного события

События могут быть
Достоверные
Невозможные
Случайные
Несовместные
Независимые
Противоположные

Достоверные события
Событие называется достоверным, если оно наступает всегда, при любом испытании.
Вероятность достоверного события всегда равна 1.
Примеры достоверных событий

Примеры достоверных событий
На игральном кубике выпадет меньше семи очков;
После лета наступит осень.

Невозможные события
Событие называют невозможным, если оно не наступает никогда, то есть благоприятных исходов для него 0.
Вероятность невозможного события равна 0 .
Примеры невозможных событий

Примеры невозможных событий
Падение монеты на ребро
Выпадение на игральной кости семерки

Случайные события
Событие называется случайным, если при одних и тех же условиях оно может как произойти, так и не произойти.
Примеры случайных событий

Примеры случайных событий
Выпадение на игральном кубике четного числа очков;
Выпадение орла при бросании монеты;
Выигрышное сочетание чисел на карточках русского лото.

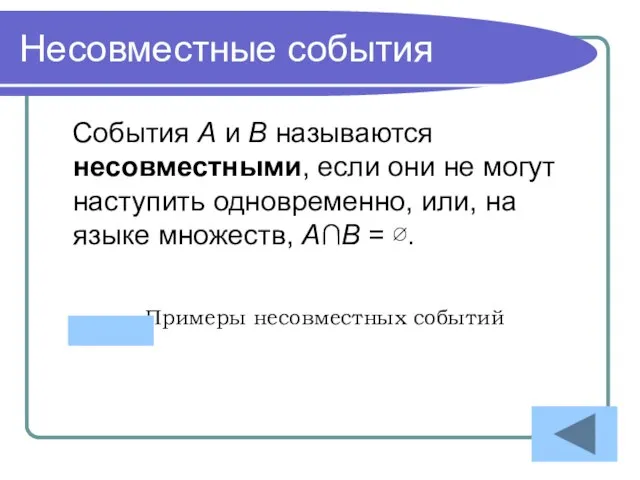
Несовместные события
События A и B называются несовместными, если они не могут наступить одновременно, или, на языке множеств, A∩B = ∅.
Примеры несовместных событий

Примеры несовместных событий
При бросании двух кубиков выпадение нечетной суммы очков и равных чисел на обоих кубиках;
Из короба с разноцветными шарами вытащить 2 шара. Несовместными будут события: оба шара красные и оба шара синие.

Независимые события
События A и B называются независимыми, если вероятность их произведения равна произведению их вероятностей: P(AB) = P(A)⋅P(B).
Примеры независимых событий

Примеры независимых событий
На обоих кубах выпадет шестерка;
При подбрасывании двух монет выпадут два орла;
При вытаскивании двух шаров из урны оба шара будут красными.

Противоположные события
С каждым событием A связано противоположное событие, состоящее в том, что событие A не осуществляется.
Противоположные события, очевидно, несовместны.
Сумма вероятностей противоположных событий равна 1
Примеры противоположных событий

Примеры противоположных событий
На кубике выпадет четное число и на кубике выпадет нечетное число;
Монета упала орлом вверх и монета упала вверх решкой;
Лампа горит и лампа не горит.

Примеры задач на вычисление
вероятностей случайных событий
З а д а ч а № 1.
Бросаются два кубика. Найти вероятность того, что сумма выпавших очков равна 6.
Р е ш е н и е .

Решение задачи №1 ( н а ч а л о)
Бросаются два кубика. Найти вероятность того, что сумма выпавших очков равна 6.
Результат каждого бросания – это пара чисел (a, b), где a и b – числа от 1 до 6. Поэтому все поле событий состоит из 6х6 = 36 элементов

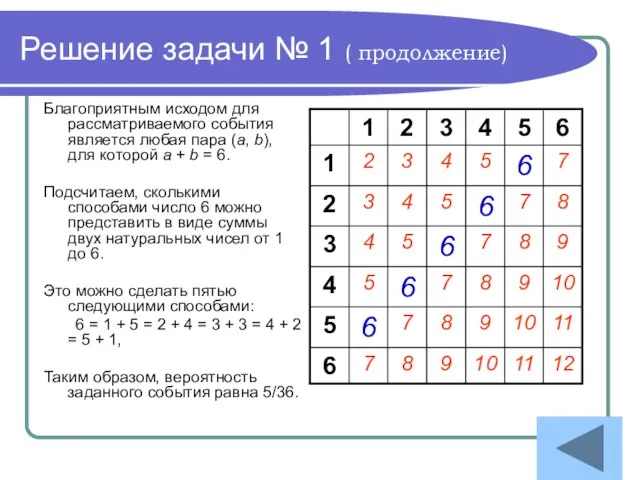
Решение задачи № 1 ( продолжение)
Благоприятным исходом для рассматриваемого события является любая пара (a, b), для которой a + b = 6.
Подсчитаем, сколькими способами число 6 можно представить в виде суммы двух натуральных чисел от 1 до 6.
Это можно сделать пятью следующими способами:
6 = 1 + 5 = 2 + 4 = 3 + 3 = 4 + 2 = 5 + 1,
Таким образом, вероятность заданного события равна 5/36.

Примеры задач на вычисление
вероятностей случайных событий
З а д а ч а № 2.
Один стрелок делает 80% попаданий, а другой (при тех же условиях стрельбы) 70%. Найти вероятность поражения цели, если оба стрелка стреляют в нее одновременно. Цель считается пораженной при попадании в нее хотя бы одной их двух пуль.
Р е ш е н и е (1 способ)
Р е ш е н и е (2 способ)
Р е ш е н и е (3 способ)

Решение задачи №2 (1 способ)
Один стрелок делает 80% попаданий, а другой (при тех же условиях стрельбы) 70%. Найти вероятность поражения цели, если оба стрелка стреляют в нее одновременно. Цель считается пораженной при попадании в нее хотя бы одной их двух пуль.
Допустим, что производится 100 двойных выстрелов. Примерно в 80 из них цель будет поражена первым стрелком. Остается около 20 выстрелов, в которых этот стрелок даст промах. Так как второй стрелок поражает в среднем 70 раз из 100 выстрелов и, значит, 7 раз из 10 выстрелов, то мы можем ожидать, что в тех 20 выстрелах, в которых первый стрелок даст промах, второму удастся поразить цель примерно 14 раз. Таким образом, при всей сотне выстрелов цель окажется пораженной 80 + 14 = 94 раза. Вероятность поражения цели при одновременной стрельбе этих двух стрелков равна поэтому 94%, или 0,94.

Решение задачи №2 (2 способ)
Один стрелок делает 80% попаданий, а другой (при тех же условиях стрельбы) 70%. Найти вероятность поражения цели, если оба стрелка стреляют в нее одновременно. Цель считается пораженной при попадании в нее хотя бы одной их двух пуль.
Вероятность попадания
Первого стрелка 0,8
Второго стрелка 0,7
Вероятность не попадания
Первого стрелка 1 - 0,8 = 0,2
Второго стрелка 1 - 0,7 = 0,3
Цель будет поражена, если
первый стрелок попадет, а второй нет 0,8∙0,3 = 0,24
второй стрелок попадет, а первый нет 0,7∙0,2 = 0,14
оба стрелка попадут 0,8∙0,7 = 0,56
Значит, цель будет поражена с вероятностью
0,24 + 0,14 + 0,56 = 0,94

Решение задачи №2 (3 способ)
Один стрелок делает 80% попаданий, а другой (при тех же условиях стрельбы) 70%. Найти вероятность поражения цели, если оба стрелка стреляют в нее одновременно. Цель считается пораженной при попадании в нее хотя бы одной их двух пуль.
Вероятность попадания
Первого стрелка 0,8
Второго стрелка 0,7
Вероятность не попадания
Первого стрелка 1 - 0,8 = 0,2
Второго стрелка 1 - 0,7 = 0,3
Цель не будет поражена, если
оба стрелка не попадут 0,2∙0,3 = 0,06
Значит, цель будет поражена с вероятностью
1 - 0,06 = 0,94

Условная вероятность
Условной вероятностью события В при условии А называют отношение
Вероятность события В в новых условиях: когда уже известно, что событие А произошло.

Условная вероятность
Формула вычисления вероятности
события В при условии, что произошло
событие А, но могло иметь место еще и событие С.
Пример использования такой обобщенной формулы
рассмотрен далее.

Примеры задач на вычисление
вероятностей случайных событий
З а д а ч а № 3.
Пусть в некотором классе 25 учеников, из них
2 "отличника",
12 "твердых хорошистов",
9 "троечников",
а остальные 2 – "отстающие".
Проверяя контрольную работу, учитель поставил 5 за одну работу, которая оказалась неподписанной. Прав ли он, считая, что она принадлежит "отличнику", если вероятность получения пятерки соответственно равна:
Отличник 0,9
Хорошист 0,7
Троечник 0,3
Отстающий 0,1?
Р е ш е н и е .

Решение задачи №3 ( н а ч а л о)
Если событие A – это поставленная пятерка за "анонимную" работу, то надо найти условную вероятность события P(B|A),
где B – событие, при котором неподписанная работа принадлежит одному из отличников .
буквами C, D, E обозначены события, при которых
пятерку получил соответственно
"хорошист", "троечник" и "отстающий".

Решение задачи №3 ( продолжение)
Значит,
По условию
Из 25 учеников
2 "отличника",
"хорошистов",
9 "троечников",
2 "отстающие".
Неподписанная работа принадлежит
B - одному из отличников ,
С - одному из хорошистов ,
D - одному из троечников ,
E - одному из отстающих .

Решение задачи №3 ( продолжение)
По условию
Из 25 учеников
2 "отличника",
"хорошистов",
9 "троечников",
2 "отстающие".
Неподписанная работа принадлежит
B - одному из отличников ,
С - одному из хорошистов ,
D - одному из троечников ,
E - одному из отстающих .
Учитывая то, что анонимную работу написал только один ученик, рассмотрим вероятность того, что
работу написал отличник,
а не хорошист, не троечник и не отстающий
работу написал хорошист,
работу написал троечник,
работу написал отстающий.

Решение задачи №3 ( окончание)
Подставим полученные значения в формулу