ОСНОВЫ ЛОГИКИ

ЛОГИКА
НАУКА О ФОРМАХ И СПОСОБАХ МЫШЛЕНИЯ

МЫШЛЕНИЕ осуществляется через:
Понятия
Высказывания
Умозаключения

ПОНЯТИЕ
форма мышления, которая выделяет существенные признаки предмета или класса предметов, позволяющие отличать их друг от друга
(Пример: Прямоугольник - геометрическая фигура у которой все углы прямые и противоположные стороны равны)

ВЫСКАЗЫВАНИЕ
формулировка своего понимания окружающего мира (повествовательное предложение в котором что-либо утверждается или отрицается)
(Пример: Париж – столица Франции)

ВЫСКАЗЫВАНИЕ
ИСТИННОЕ ЛОЖНОЕ
(Пример: Буква «А» - (Пример: Компьютер
гласная) был изобретен до
нашей эры)

УМОЗАКЛЮЧЕНИЕ
форма мышления, с помощью которой из одного или нескольких суждений может быть получено новое суждение
(знание или вывод)
(Пример: любая теорема)

АЛГЕБРА ЛОГИКИ
наука об общих операциях, аналогичных сложению и умножению, которые выполняются над высказываниями

Понятия алгебры логики:
Логическая переменная – это простое высказывание, содержащее только одну мысль
Обозначение: латинская буква (А, В, Х …)
Значение: ИСТИНА (1) или ЛОЖЬ (0)
Логическая функция – это составное высказывание, которое содержит несколько простых мыслей, соединенных между собой с помощью логических операций
Обозначение: F
Логические операции – логическое действие

Базовые логические операции

Таблица истинности
таблица определяющая значение сложного высказывания при всех возможных значениях простых высказываний

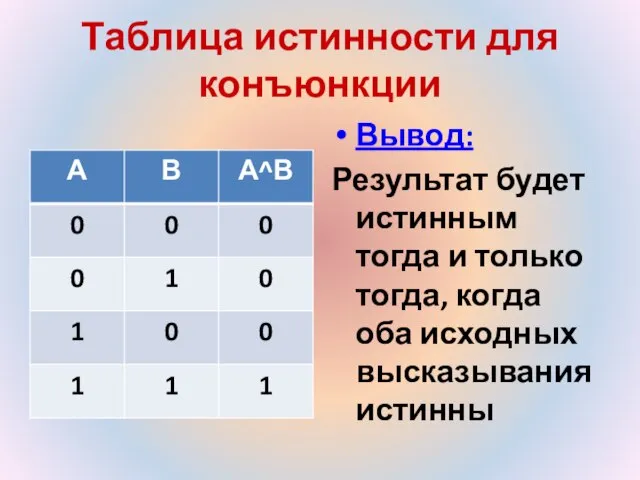
Таблица истинности для конъюнкции
Вывод:
Результат будет истинным тогда и только тогда, когда оба исходных высказывания истинны

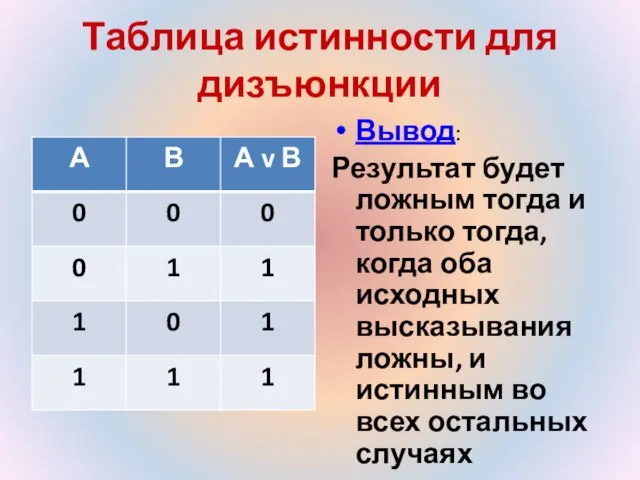
Таблица истинности для дизъюнкции
Вывод:
Результат будет ложным тогда и только тогда, когда оба исходных высказывания ложны, и истинным во всех остальных случаях

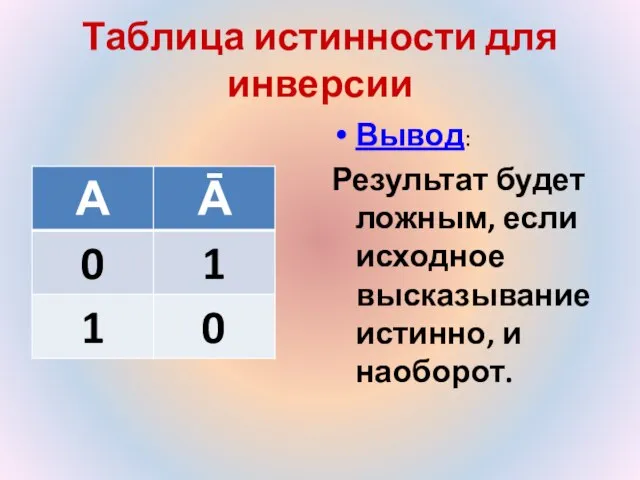
Таблица истинности для инверсии
Вывод:
Результат будет ложным, если исходное высказывание истинно, и наоборот.

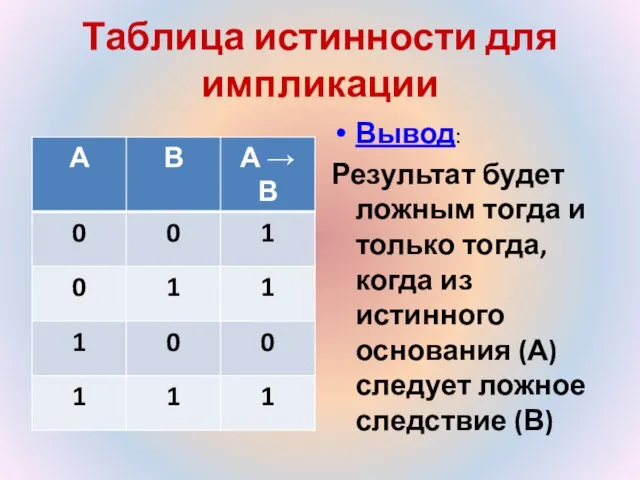
Таблица истинности для импликации
Вывод:
Результат будет ложным тогда и только тогда, когда из истинного основания (А) следует ложное следствие (В)

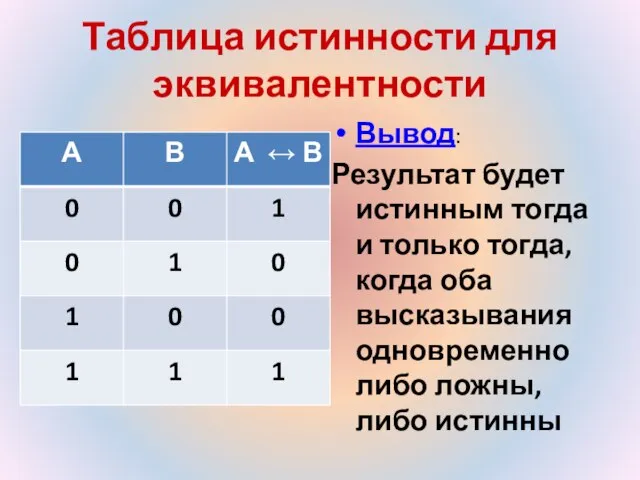
Таблица истинности для эквивалентности
Вывод:
Результат будет истинным тогда и только тогда, когда оба высказывания одновременно либо ложны, либо истинны

Если составное высказывание (логическую функцию) выразить в виде формулы, в которую войдут логические переменные и знаки логических операций, то получится
ЛОГИЧЕСКОЕ ВЫРАЖЕНИЕ
истина ложь

Порядок выполнения логических операций:
Действия в скобках
Инверсия
Конъюнкция
Дизъюнкция
Импликация
Эквивалентность

ПРИМЕР: Записать в виде логического выражения следующее высказывание: «Летом Петя поедет в деревню и, если будет хорошая погода, то он пойдет на рыбалку»
Это составное высказывание состоит из простых высказываний:
А = «Петя поедет в деревню»
В = «Будет хорошая погода»
С = «Он пойдет на рыбалку»
Записываем высказывание в виде логического выражения, учитывая порядок действий
F = A ^ (B → C)