Основы логики

ЛОГИКА -- ЭТО УЧЕНИЕ О СПОСОБАХ РАССУЖДЕНИЙ И ДОКАЗАТЕЛЬСТВ, НАУКА О ЗАКОНАХ И ФОРМАХ МЫШЛЕНИЯ
«LOGOS» -- СЛОВО, МЫСЛЬ, ПОНЯТИЕ, РАССУЖДЕНИЕ, ЗАКОН

РАЗВИТИЕ ЛОГИКИ:
СОКРАТ
ПЛАТОН
АРИСТОТЕЛЬ
Древняя Греция:
XVII в. Готфрид Вильгельм Лейбниц: «Рассуждения могут быть сведены к механическому выполнению определенных действий по установленным правилам»
XIX в. – логика формируется как самостоятельный раздел математики. Джордж Буль: «Математический анализ логики» - 1847г., «Исследование законов мышления, базирующихся на математической логике и теории вероятности» - 1854г.

ОСНОВНЫЕ ПОНЯТИЯ ЛОГИКИ:
ВЫСКАЗЫВАНИЕ – ПОВЕСТВОВАТЕЛЬНОЕ ПРЕДЛОЖЕНИЕ, В КОТОРОМ ЧТО-ЛИБО УТВЕРЖДАЕТСЯ ИЛИ ОТРИЦАЕТСЯ.
Свойство высказывания: ПРО ВЫСКАЗЫВАНИЕ ВСЕГДА МОЖНО СКАЗАТЬ, ИСТИННО ОНО ИЛИ ЛОЖНО

На марсе была жизнь.
Динозавры были теплокровными животными.
1 марта 1 года новой эры на территории современной Москвы прошел дождь.
В тихом омуте черти водятся
С помощью философского камня можно превратить свинец в золото.

Высказывание может принимать одно из двух возможных логических значений: ИСТИНА или ЛОЖЬ
ИСТИНА
ЛОЖЬ
ЛОГИЧЕСКИЕ ПОСТОЯННЫЕ
Или
ЛОГИЧЕСКИЕ КОНСТАНТЫ

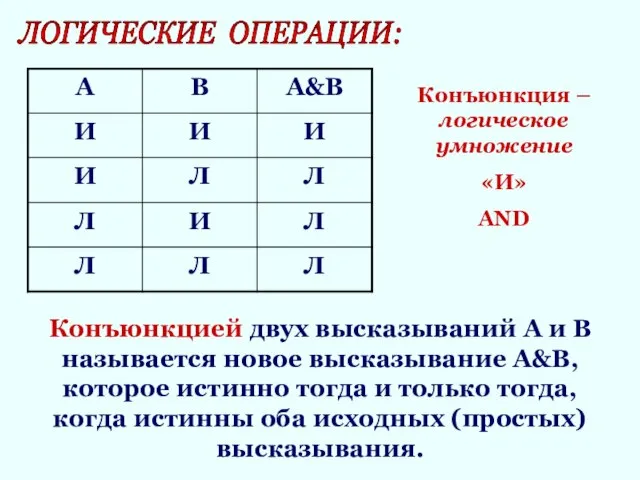
ЛОГИЧЕСКИЕ ОПЕРАЦИИ:
Конъюнкцией двух высказываний А и В называется новое высказывание А&В, которое истинно тогда и только тогда, когда истинны оба исходных (простых) высказывания.
Конъюнкция – логическое умножение
«И»
AND

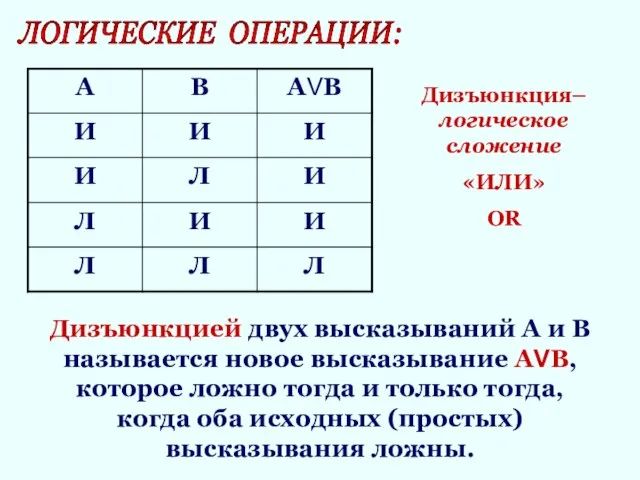
ЛОГИЧЕСКИЕ ОПЕРАЦИИ:
Дизъюнкцией двух высказываний А и В называется новое высказывание АVВ, которое ложно тогда и только тогда, когда оба исходных (простых) высказывания ложны.
Дизъюнкция– логическое сложение
«ИЛИ»
OR

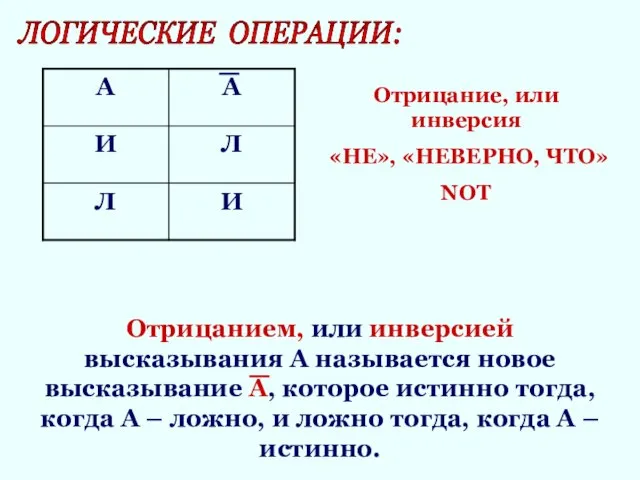
ЛОГИЧЕСКИЕ ОПЕРАЦИИ:
Отрицанием, или инверсией высказывания А называется новое высказывание А, которое истинно тогда, когда А – ложно, и ложно тогда, когда А – истинно.
Отрицание, или инверсия
«НЕ», «НЕВЕРНО, ЧТО»
NOT

Логическое выражение – форма записи высказывания.
Логические выражения составляются из простых высказываний с помощью логических операций, а так же операций отношения (>, <, >=, <=, <>) и круглых скобок.
Логическое выражение может иметь значение «Истина» или «ЛОЖЬ» (обозначение 1 и 0 соответственно)
Пример 1. Найдите значение логического выражения: (3x – 2y > 5) AND (x-y <= 0) OR (2x + 5y < 4) при х = 2, у = 3.

ПРИОРИТЕТ ОПЕРАЦИЙ:
-- находятся значения выражений в скобках;
-- выполняются логические операции:
- отрицание (NOT),
- конъюнкция (AND),
- дизъюнкция (OR).

НАЙДИТЕ ЗНАЧЕНИЯ ЛОГИЧЕСКИХ ВЫРАЖЕНИЙ:
1. (3x – 2y >5) AND (x-y <= 0) OR (2x +5y <4),
при x = 2, y = 3.
2. (5a -8b >12) OR (a + b <= 4) AND (2ab < 3) OR (8b – a =4),
при a= 5, b = 4.
3. NOT (12m < 4n) AND (3n +2 > 2m) OR (5n -2m <= 7),
при m = 2, n = 5

ПРАКТИЧЕСКОЕ ЗАДАНИЕ:
В текстовом процессоре MS Word изобразите таблицы (таблицу) истинности для логических операций:
КОНЪЮНКЦИИ, ДИЗЪЮНКЦИИ, ИНВЕРСИИ.
Полученный файл сохраните на рабочем столе под своей фамилией.

ЗАДАНИЕ НА ДОМ:
Выучить основные понятия математической логики: -- определения основных логических операций, таблицы истинности, -- приоритет операций;
-- придумайте 3 логических выражения и найдите значение каждого из них (задание оформить в тетради).

Утверждение, заключенное в красную рамку на этом слайде, истинно.
Утверждение, заключенное в синюю рамку на этом слайде, ложно.

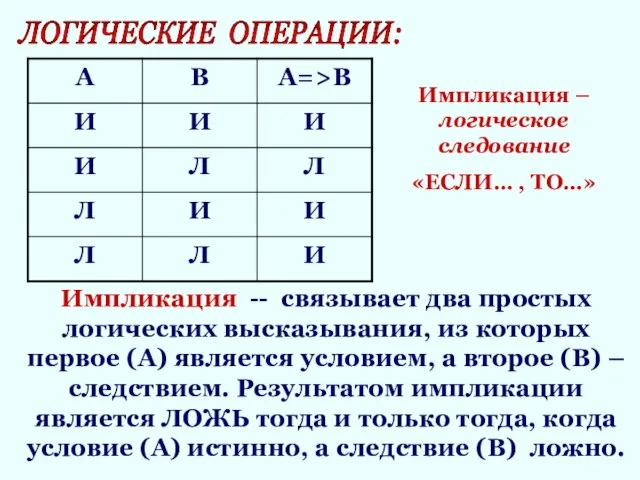
ЛОГИЧЕСКИЕ ОПЕРАЦИИ:
Импликация -- связывает два простых логических высказывания, из которых первое (А) является условием, а второе (В) – следствием. Результатом импликации является ЛОЖЬ тогда и только тогда, когда условие (А) истинно, а следствие (В) ложно.
Импликация – логическое следование
«ЕСЛИ… , ТО…»

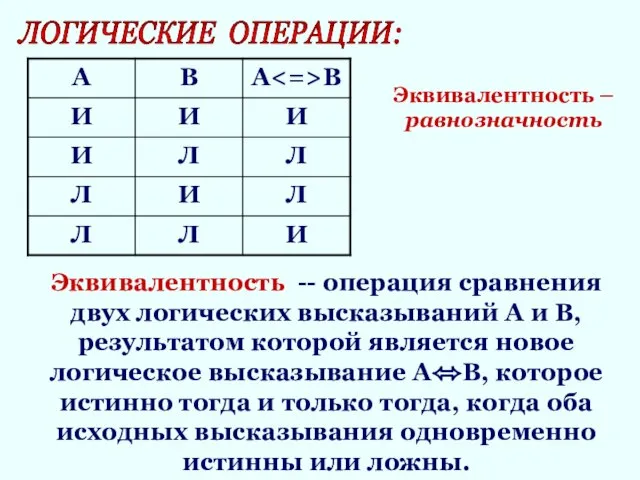
ЛОГИЧЕСКИЕ ОПЕРАЦИИ:
Эквивалентность -- операция сравнения двух логических высказываний А и В, результатом которой является новое логическое высказывание А⬄В, которое истинно тогда и только тогда, когда оба исходных высказывания одновременно истинны или ложны.
Эквивалентность – равнозначность