Основы логики и логические основы компьютера

Логика –это наука о формах и способах мышления;особая форма мышления.
Понятие - это форма мышления, фиксирующая основные, существенные признаки объекта.
Высказывание – форма мышления, в которой что-либо утверждается или отрицается о свойствах реальных предметов и отношениях между ними. Высказывание может быть либо истинно, либо ложно.

Логика
Высказывания:
Истинные(1) и ложные (0);
Простые и сложные;
Общие, частные и единичные.

Высказывания.
Высказывания бывают общими, частными или единичными. Общее высказывание начинается (или можно начать) со слов: все, всякий, каждый, ни один. Частное высказывание начинается ( или можно начать) со слов: некоторые, большинство и т.п. Во всех других случаях высказывание является единичным.

Примеры высказываний:
Пример 1. Определить тип высказывания (общее, частное, единичное).
«Все рыбы умеют плавать».
Ответ: общее высказывание.
«Некоторые медведи -бурые».
Ответ: частное высказывание.
«Буква А – гласная».
Ответ: единичное высказывание.

Примеры высказываний:
Пример 2. Из двух простых высказываний постройте сложное высказывание, используя логические связки «И», «ИЛИ»:
Все ученики изучают математику. Все ученики изучают литературу.
Все ученики изучают математику и литературу.

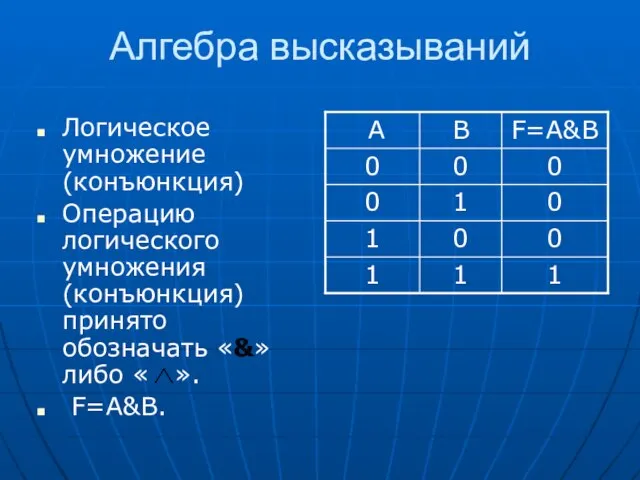
Алгебра высказываний
Логическое умножение (конъюнкция)
Операцию логического умножения (конъюнкция) принято обозначать «&» либо « ».
F=A&B.

Логическое сложение
Дизъюнкция
Истинно тогда, когда истинно хотя бы одно из входящих в него простых высказываний.
F=A B

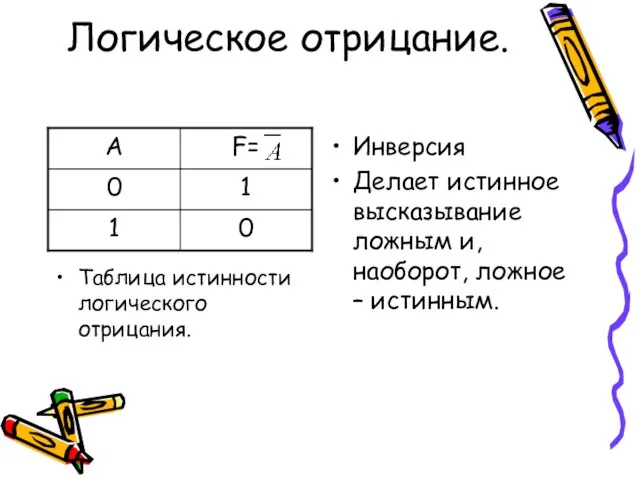
Логическое отрицание.
Инверсия
Делает истинное высказывание ложным и, наоборот, ложное – истинным.
Таблица истинности логического отрицания.

Логические законы и правила преобразования логических выражений.
Закон тождества. Всякое высказывание тождественно самому себе.
Закон непротиворечия.
А=А
А& =0

Логические законы и правила преобразования логических выражений.
Закон исключения третьего.
Закон двойного отрицания.
Закон де Моргана.
А =1

Логические законы и правила преобразования логических выражений.
Закон коммутативности. В алгебре высказываний можно менять местами логические переменные при операциях логического умножения и логического сложения:

Логические законы и правила преобразования логических выражений.
Закон ассоциативности. Если в логическом выражении используются только операция логического умножения или только операция логического сложения, то можно пренебрегать скобками или произвольно их расставлять:

Логические законы и правила преобразования логических выражений
Закон дистрибутивности. В алгебре высказываний можно выносить за скобки как общие множители, так и общие слагаемые:

Логические основы устройства компьютера
Базовые логические элементы.
Логический элемент «И» - логическое умножение.
Логический элемент «ИЛИ» - логическое сложение.
Логический элемент «НЕ» - инверсия.

Логический элемент «И».
Логический элемент «И». На входы А и В логического элемента подаются два сигнала (00, 01, 10 или 11).
На выходе получается сигнал 0 или 1 в соответствии с таблицей истинности операции логического умножения.
И
А (0,0,1,1)
F (0,0,0,1)
В (0,1,0,1)

Логический элемент «ИЛИ».
На входы А и В логического элемента подаются два сигнала (00, 01, 10 или 11).
На входе получается сигнал 0 или 1 в соответствии с таблицей истинности операции логического сложения.
ИЛИ
А (0,0,1,1)
F (0,1,1,1)
В (0,1,0,1)

Логический элемент «НЕ»
На вход А логического элемента подается сигнал 0 или 1.
На входе получается сигнал 0 или 1 в соответствии с таблицей истинности инверсии.
НЕ
А (0,1)
F (1,0)

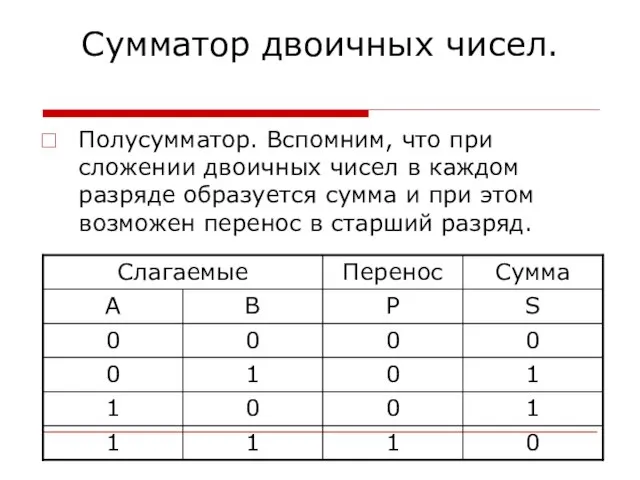
Сумматор двоичных чисел.
Полусумматор. Вспомним, что при сложении двоичных чисел в каждом разряде образуется сумма и при этом возможен перенос в старший разряд.

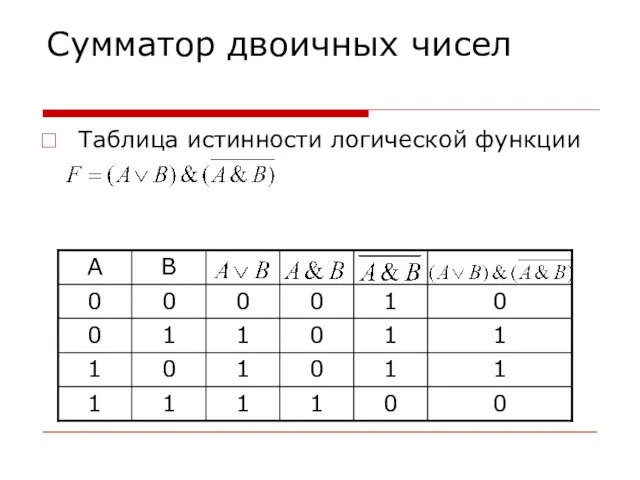
Сумматор двоичных чисел
Таблица истинности логической функции

Полный однозарядный сумматор.
Полный однозарядный сумматор должен иметь три входа: А,В- слагаемые и Р0 – перенос из младшего разряда и два выхода: сумму S и перенос Р.
Идея построения полного сумматора точно такая же, как и полусумматора. Перенос реализуется путем логического сложения результатов попарного логического умножения входных переменных. Формула переноса получает следующий вид:

Многозарядный сумматор.
Многозарядный сумматор процессора состоит из полных однозарядных сумматоров.
На каждый разряд ставится однозарядный сумматор, причем выход (перенос) сумматора младшего разряда подключается ко входу сумматора старшего разряда.