Основы логики. Высказывания.

Алгебра — это наука об общих операциях, аналогичных сложению и умножению, которые выполняются не только над числами, но и над другими математическими объектами, в том числе и над высказываниями. Такая алгебра называется алгеброй логики.
Алгебра логики отвлекается от смысловой содержательности высказываний и принимает во внимание только истинность или ложность высказывания.

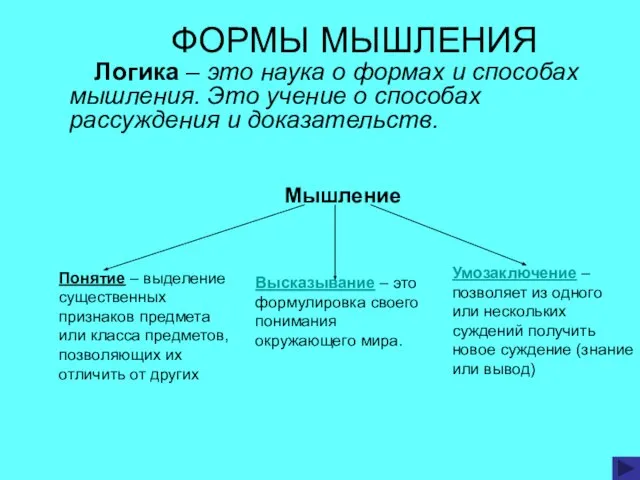
ФОРМЫ МЫШЛЕНИЯ
Логика – это наука о формах и способах мышления. Это учение о способах рассуждения и доказательств.
Мышление
Понятие – выделение существенных признаков предмета или класса предметов, позволяющих их отличить от других
Умозаключение – позволяет из одного или нескольких суждений получить новое суждение (знание или вывод)
Высказывание – это формулировка своего понимания окружающего мира.

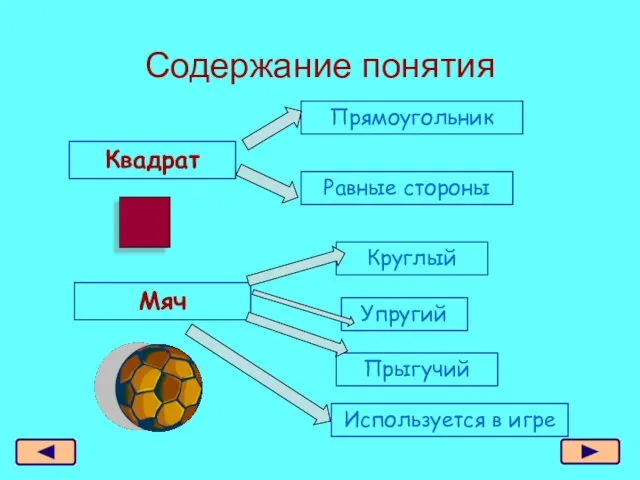
Содержание понятия

Высказывание
Высказывание — повествовательное предложение, в котором что-либо утверждается или отрицается.
По поводу высказывания можно сказать, истинно оно или ложно.
Истинным будет высказывание, в котором связь понятий правильно отражает свойства и отношения, реальных вещей. Ложным высказывание будет в том случае, когда оно противоречит реальной действительности.

Какие из предложений являются высказываниями? Определите их истинность.
Какой длины эта лента?
Прослушайте сообщение.
Делайте утреннюю зарядку!
Назовите устройство ввода информации.
Кто отсутствует?
Париж — столица Англии.
Число 11 является простым.
4 + 5=10.
Без труда не вытащишь и рыбку из пруда.
Сложите числа 2 и 5.
Некоторые медведи живут на севере.
Все медведи — бурые.
Чему равно расстояние от Москвы до Ленинграда.

Умозаключение
Умозаключение — это форма мышления, с помощью которой из одного или нескольких суждений может быть получено новое суждение (знание или вывод).
Новое суждение можно получить с помощью логических действий – операций.

.
Получить высказывание:
«Этот треугольник равносторонний», путем умозаключений.
ФОРМЫ МЫШЛЕНИЯ
Все углы равнобедренного треугольника равны

Логические выражения и операции
Логическая переменная — это простое высказывание, содержащее только одну мысль. Ее символическое обозначение - латинская буква (например, A,B,X,Y и т.д.). Значением логической переменной могут быть только константы ИСТИНА и ЛОЖЬ (1 и 0).
Составное высказывание — логическая функция, которая содержит несколько простых мыслей, соединенных между собой с помощью логических операций. Ее символическое обозначение —F(A,B,...).
На основании простых высказываний могут быть построены составные высказывания.
Логические операции — логическое действие.

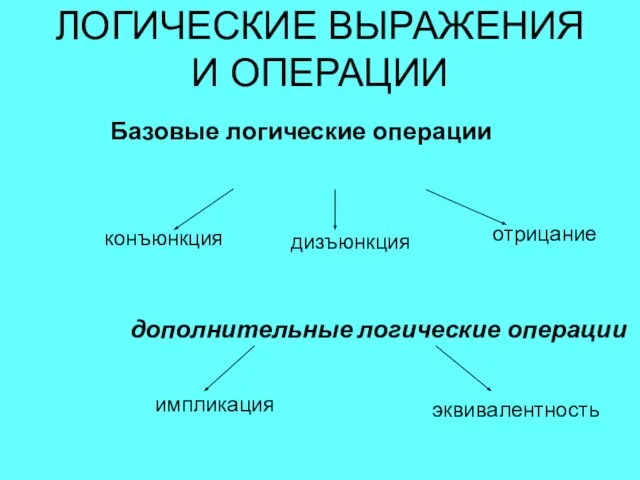
Базовые логические операции
ЛОГИЧЕСКИЕ ВЫРАЖЕНИЯ И ОПЕРАЦИИ
конъюнкция
дизъюнкция
отрицание
импликация
дополнительные логические операции
эквивалентность

Логические операции
Конъюнкция – логическое умножение (И)
Обозначение: ^ или &
Пример: «За окном осень и на улице пасмурно»
А - За окном осень
В - На улице пасмурно
А&В

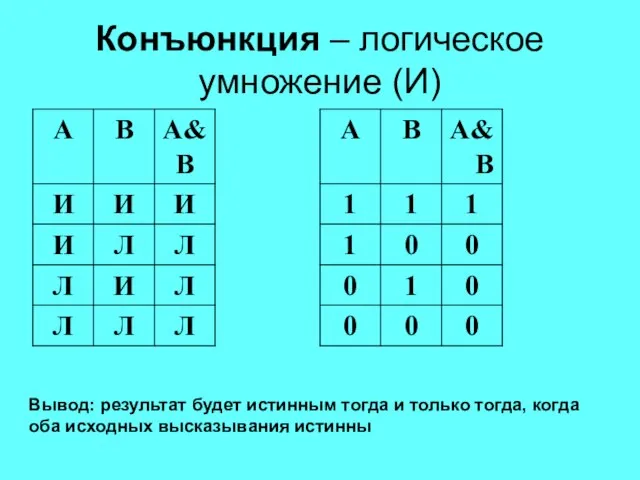
Конъюнкция – логическое умножение (И)
Вывод: результат будет истинным тогда и только тогда, когда оба исходных высказывания истинны

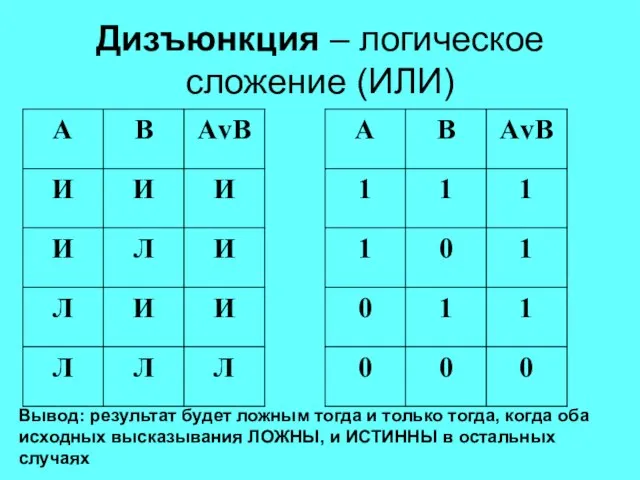
Логические операции
Дизъюнкция – логическое сложение (ИЛИ)
Обозначение: V
Пример: «В буфете я попью чаю или сока»
А - В буфете я попью чаю
В - В буфете я попью сока
А v В

Дизъюнкция – логическое сложение (ИЛИ)
Вывод: результат будет ложным тогда и только тогда, когда оба исходных высказывания ЛОЖНЫ, и ИСТИННЫ в остальных случаях

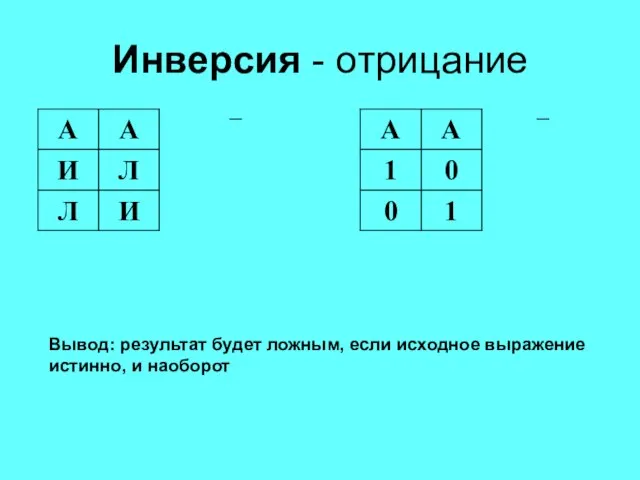
Логические операции
Инверсия - отрицание
Обозначение: ¬ или ¯
Пример: «Этот урок не последний»
А - Этот урок последний.
¬ А

Инверсия - отрицание
Вывод: результат будет ложным, если исходное выражение истинно, и наоборот

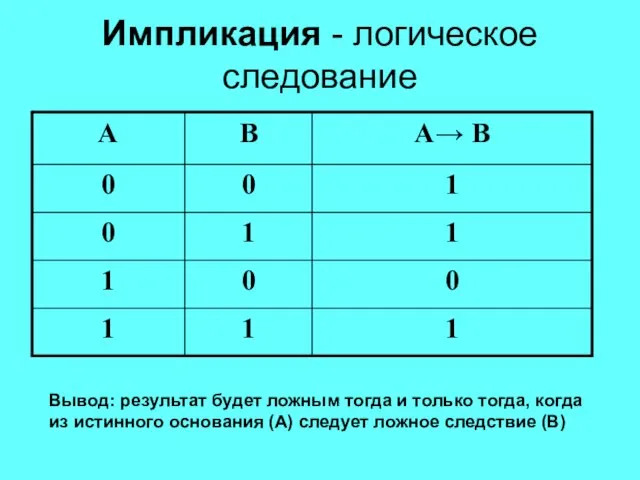
Логические операции
Импликация - логическое следование
Обозначение: →
Пример: «Если число делится на 2, то оно - четное.
А - число делится на 2
В – число четное
А→В

Импликация - логическое следование
Вывод: результат будет ложным тогда и только тогда, когда из истинного основания (А) следует ложное следствие (В)

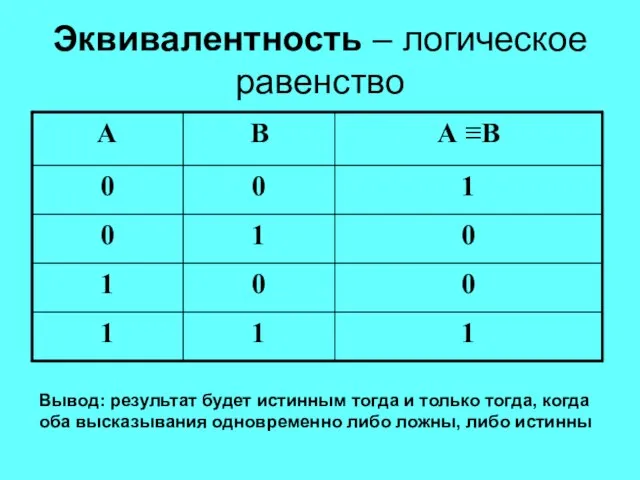
Логические операции
Эквивалентность – логическое равенство
Обозначение: ↔ или ≡
Пример: «Водительские права можно получить тогда и только тогда, когда тебе исполнится 18 лет»
А - Водительские права получить
В - тебе исполнится 18 лет
А≡В

Эквивалентность – логическое равенство
Вывод: результат будет истинным тогда и только тогда, когда оба высказывания одновременно либо ложны, либо истинны

«Летом Петя поедет в деревню,
и если будет хорошая погода,
то он пойдет на рыбалку».
ЛОГИЧЕСКИЕ ВЫРАЖЕНИЯ И ОПЕРАЦИИ
Простые высказывания
«Будет хорошая погода»
«Он пойдет на рыбалку»
«Петя поедет в деревню»
А = Петя поедет в деревню;
В = Будет хорошая погода;
С = Он пойдет на рыбалку.
F= А&(В?С)